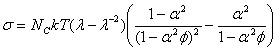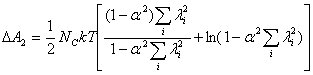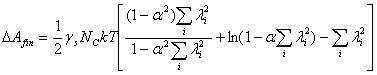Сеничев В.Ю., Терешатов В.В., Макарова М.А., Волкова Е.Р., Красносельских С.Ф.

Институт технической химии Уральского отделения РАН, Пермь, Россия

Обобщенный подход для описания кривых напряжение-деформация сшитых эластомеров

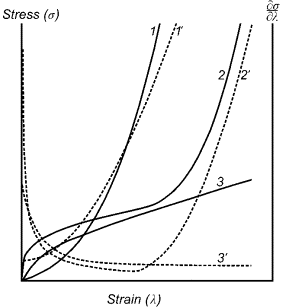
Рассмотрены все возможные варианты графиков зависимостей напряжения от деформации для эластомера при простом растяжении. Они могут быть трех различных типов (рис.1). Во-первых, это кривые вогнутого типа (кривая 1 на рис.1), которые могут наблюдаться для резин на основе высокомолекулярных каучуков. Во-вторых, кривые с перегибом (кривая 2 на рис.1), типичные для полиэфируретанов и ряда сшитых каучуков. Третий тип кривых (кривая 3 на рис.1) - это кривые выпуклого типа, характерные, например, для полибутадиенуретанов.

В рамках классической теории эластичности зависимость напряжение-деформация при простом растяжении имеет вид:

(1)

где s - напряжение, рассчитанное на начальное сечение образца, k-константа Больцмана, T –абсолютная температура, l-степень деформирования (отношение длины растянутого образца к исходной длине) - число эластически активных цепей на единицу объема образца.

Для описания кривых растяжения при небольших деформациях, обычно до 200-250%, используется также уравнение Муни-Ривлина:

(2)

где С₁,С₂ – структурные параметры.

Уравнения (1) и (2) соответствуют выпуклой форме кривых. Естественно, они не описывают зависимости напряжения от деформации с резким подъемом напряжения при больших деформациях (обычно λ>5), как на кривой 2, рис.1.

Кривые с эффектом упрочнения могут быть описаны, используя концепцию конечной растяжимости полимерных цепей, в рамках которой даются границы применимости статистики Гаусса при оценке свободных конформаций полимерных цепей.

Проведен анализ теории Эдвардса-Вилгиса, использующей концепцию конечной растяжимости полимерных цепей. В данной теории выражение для зависимости напряжения от деформации при простом растяжении образца таково[1]:

,

(3)

где -коэффициент нерастяжимости полимерной цепи, .

Рис.1 Основные типы графиков зависимостей при растяжении сшитых эластомеров: 1-кривая вогнутая, 2 – кривая с перегибом, 3 - кривая выпуклая. 1´,2´,3´ – соответствующие производные.

Численный анализ данного уравнения, проведенный авторами, показал серьезные ограничения его применимости, что связано с положением точки перегиба на кривой зависимости напряжения от деформации. Как оказалось, данное уравнение в исходном виде дает грубые отклонения от эксперимента практически на всех участках графика зависимости напряжения от деформации. Причинами отклонений является отсутствие в уравнении (3) учета вклада стерических затруднений в эластическую реакцию цепи и недостаточный учет негомогенности топологии реальных сеток.

Предложен обобщающий подход, в котором учет вклада стерических затруднений осуществляется с использованием МСС-модели Эрмана-Моннери [2], а корректировка вклада эффекта конечной растяжимости цепей производится с использованием структурного параметра, зависящего от топологии сетки.

Было установлено, что вклад конформационных изменений и стерических затруднений в эластическую реакцию сетки можно отразить следующим аппроксимирующим выражением:

(4)

Если заменить на в данном уравнении, то оно станет эквивалентно уравнению Муни-Ривлина. Этот факт, на наш взгляд, свидетельствует о единстве разных подходов теории эластичности в описании выпуклых кривых σ-λ. Выявленное же отличие характеризует более интенсивное изменение дифференциального модуля некоторых образцов на начальном этапе деформирования, чем это может быть описано уравнением Муни-Ривлина [3].

Учет вклада эффекта конечной растяжимости цепи в эластическую реакцию цепи в рамках настоящей работы был откорректирован, используя отдельный учет этого эффекта. Так, в рамках теории Эдвардса-Вилгиса, величина свободной энергии высокоэластичности записывается следующим образом:

(5)

Вклад в DA₂ свободной энергии за счет изменения конформации полимерных цепей DA₃ в соответствии с классической теорией эластичности:

.

Из выражения (5) вычтем и получим изменение энергии , обусловленное только эффектом конечной растяжимости цепей при деформации образца:

Предположим, что только некоторая часть цепей по мере деформирования переходит в перенапряженное состояние. Это можно учесть корректирующим параметром γ_s :

Дифференцирование последнего выражения с учетом выражения (4) дает обобщенное выражение для зависимости σ-λ при простом растяжении для сетки с трехфункциональными узлами (f_n=3):

(6)

Очевидно, что при g_s=0 это выражение будет соответствовать скорректированной МСС-модели, а при g_s=1 будет отличаться от выражения (3) составляющей напряжения, не связанной с эффектом конечной растяжимости цепи.

Физический смысл параметра a связан с максимальной степенью растяжения λ_max, при которой конформации цепей уже не подчиняются распределению Гаусса. Для одиночной полимерной цепи дано следующее выражение . При больших деформациях энтропия уменьшается и когда полимерная цепь полностью вытянута, нет больше свободных конформаций, которые бы могла принимать полимерная цепь.

Экспериментальная проверка разработанного подхода проведена была с использованием образцов сшитого полиуретана с аморфной структурой на основе политетраметиленгликоля, толуилендиизоцианата и полиоксипропилентриола.

Работа была выполнена благодаря поддержке РФФИ (проект 13-03-00101).

Литература

1. Christenson, E.M.; Anderson, J.M.; Hiltner, A.; Baer, E. Relationship between nanoscale deformation processes and elastic behavior of polyurethane elastomers. Polymer 2005, 46, 11744-11754.

2. Erman, B.; Monnerie, L.: Theory of elasticity of amorphous networks: effect of constraints along chain. Macromolecules 1989, 22, 3342-3348.

3. Tereshatov, V.V.; Senichev, V.Yu. Stress-strain behavior of cross-linked polybutadiene urethanes. Polym. Sci. 1995, A37, 702-705.