Докторант 2 курса, магистр Исмаилова А.А.,

д.т.н., профессор Адамов А.А.

Евразийский национальный университет им. Л.Н. Гумилева,

Астана, Казахстан

Теоретические основы математического

моделирования водных экосистем

Целью данной работы является разработка методов и моделей прогнозирования динамики концентрации загрязняющих веществ в воде для информационных систем экологического мониторинга водных экосистем Республики Казахстан.

Академик А.Н.Тихонов дает следующее определение: "Математическая модель - приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики". Он выделяет четыре этапа математического моделирования. Первый - "формулирование законов, связывающих основные объекты модели", второй - "исследования математических задач, к которым приводят математические модели", третий - "...выяснение..., согласуются ли результаты наблюдений с теоретическими следствиями модели в пределах точности наблюдений", четвертый - "последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели". [1]

Видное место в моделировании водных экосистем занимает В.А.Костицын (Kostitzin, 1937). Он исследовал различные математические модели функционирования популяций и сообществ водных организмов в пресных водоемах, достаточно подробно занимался моделированием прудовых хозяйств. Дальнейшие исследования первой половины двадцатого века привели к большому количеству моделей популяций и сообществ водных организмов, а также созданию методологии моделирования водных экосистем.

В настоящее время существует три основных направления моделирования функционирования экосистем: а) аналитическое: агрегированные и демографические модели; методология системы Лотки - Вольтерра; б) имитационное моделирование; в) методология Ивлева - Меншуткина - Холдинга.

Общая модель водной экосистемы. Агрегированной моделью водной экосистемы служит система уравнений в частных производных параболического типа, условно называемая «диффузия - конвекция - реакция» [2, 3], следующего вида:

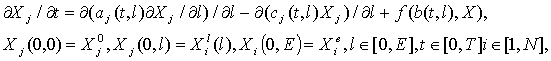(1.1)

где - биомассы или численности экологически однородных группировок, - функция, описывающая скорость продуцирования биомассы, - матрицы коэффициентов диффузии, конвекции и реакции соответственно, экологический смысл приведенных которых рассматривается далее. Согласно феноменологической идеологии, положенной в основу (1.1) в моделировании водной экосистемы выделяется два аспекта: моделирование абиотических свойств водной экосистемы и моделирование состояния сообщества популяций. Содержание задач первого аспекта отражает феномены «физической диффузии и конвекции», второго аспекта - реакции, или (используя экологическую терминологию) - «продукции-потребления». Это классическая точка зрения, основанная на результатах исследования относительно малопроточных водоемов. Необходимо представить матрицы коэффициентов в следующем виде:

(1.2)

Учет феноменологии, выражаемой в виде (1.2) переводит классическую систему (1.1) в систему нелинейной диффузии, которая описывает динамику такого класса объектов, как диссипативные структуры. Векторная форма синтеза (1.1) и (1.2) может быть представлена как:

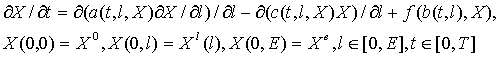(1.3)

Дальнейшее обсуждение свойств (1.1) - (1.3) целесообразно продолжить после исследования функции «продукции-потребления» .

В области математического моделирования биологических объектов методология системы Лотки - Вольтерра позволяет получить довольно агрегированное описание динамики экосистем и является удобным аппаратом для проведения аналитических исследований. Основная литература, отражающая исследование экосистем, посвящена этому направлению и касается вопросов устойчивости квазиреальных сообществ. Логистическое уравнение

(1.4) где X - обилие популяции, b - биотический потенциал, К - емкость среды.

Система Лотки - Вольтерра

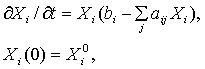(1.5) где - матрица конкуренции. Для повышения адекватности системы Лотки-Вольтерра рядом авторов предлагается следующая модификация системы Лотки-Вольтерра

(1.6)

Соотношение (1.6), фактически, представляет уравнение Михаэлиса-Ментен, по сути дела, являющегося аппроксимацией решения (1.4). В ряде работ показано, что система (1.5) - (1.6) при определенных значениях параметров имеет решение, обладающее странным аттрактором.

В ряде работ, где учитываются механизмы запаздывания, используются модификации (1.4) или (1.5), путем включения соответствующих членов. Например, (1.7)

При имитационном моделировании качества воды необходимо совместное описание гидрофизических и химико-биологических процессов. Задача моделирования заключается в том, чтобы научиться предвидеть, возможно, более отдалённые последствия вмешательства человека в установившийся в природе круговорот веществ и уметь нейтрализовать нежелательные результаты. Водная экосистема является элементом системы более высокого порядка – биосферы.

Остановимся на описании водных потоков и в качестве примера Упрощённое уравнение для расчёта температурного режима реки. Температурный режим водных потоков описывается уравнением теплопроводности Фурье –Кирхгофа:

,

где x, y, z – декартовы координаты, t – время, T – температура, - составляющие вектора скорости, с - удельная теплоёмкость воды, p - плотность среды, - коэффициенты теплопроводности, Sv - внутренние источники тепла. Для водных потоков в руслах рек и каналов обычно принимают x-овую и z-овую составляющие вектора скорости равными нулю и тоже равным нулю. [4]

Известно, что основная задача научного анализа – выделить реальные движения из множества мысленно допустимых, сформулировать принципы их отбора. На данном этапе нашей работы ведется анализ теоретических основ математического моделирования водных экосистем.

Литература:

1. Математическая энциклопедия / Гл.Ред. И.М.Виноградов. –М.: Изд-во "Советская энциклопедия", 1982. – Т.3. – 1183 с.

2. Зыков B.C. Моделирование волновых процессов в возбудимы средах. – М.: Наука, 1984 –168 с.

3. Математическое моделирование. Процессы в сложных экономических и экологических системах – М.: Наука, 1986 – 296 с.

4. Белолипецкий В.М., Шокин Ю. И. Математические модели в задачах охраны окружающей среды.. – Новосибирск: Изд-во «ИНФОЛИО-пресс», 1997. – 240 с.