Економічні
науки/8. Математичні методи в економіці
К.ф.-м.н. Мельник О.О.
ДВНЗ "КНЕУ імені
Вадима Гетьмана", Україна
Умови досягнення оптимального прибутку виробництва із застосуванням
комплекснозначних функцій
Сьогодні складно уявити собі ряд
наук без застосування комплексних чисел [1]. Теорія електротехніки, електромеханіки, радіотехніки,
літакобудування та інших наук неможлива без застосування моделей у вигляді комплексних чисел.
Зауважимо, що такі характеристики комплексного числа як його модуль і аргумент,
мають сенс тільки тоді, коли складові комплексного числа відображають загальний
зміст.
Наприклад, товар є
носієм двох складових:
споживчих властивостей,
об'єктивно властивих товару, і ціни -
грошової оцінки споживчих властивостей товару конкретним
споживачем.
Сьогодні
комплекснозначна економіка являє собою досить розвинений математичний
інструмент, який спирається, в тому числі, і на економетрику комплексних
змінних [2, 3]. Оцінки цих моделей дозволяють використовувати їх в реальній
економічній практиці. Але ці оцінки є точковими, а теоретичне та методичне
обґрунтування інтервальних оцінок комплекснозначних моделей поки не відомі, що
звужує межі застосування комплекснозначної економіки в реальній практиці. У
зв'язку з цим задача побудови інтервальних оцінок комплекснозначних моделей
економіки представляється актуальною.
Одночасно з цим,
апарат виробничих функцій недооцінений і, більшою мірою, використовується в
математичній економіці та економетриці лише в якості моделі, що дає певну
інформацію для подальших досліджень. Розробка нових моделей, що істотно
відрізняються від наявних і привносять щось нове в теорію виробничих функцій, є
актуальною проблемою.
Розглянемо степеневу функцію вигляду:
![]() (1)
(1)
де
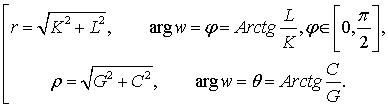
К – витрати капіталу, L - витрати праці, причому ![]() . Аргумент
. Аргумент ![]() -
це багатозначна функція, геометрично зображується багатолистою рімановою
поверхнею, її однолисту функцію отримуємо за допомогою розрізу в площині W по осі
-
це багатозначна функція, геометрично зображується багатолистою рімановою
поверхнею, її однолисту функцію отримуємо за допомогою розрізу в площині W по осі ![]() і проколом в точці w=0.
Тоді
і проколом в точці w=0.
Тоді ![]() змінюється в межах
змінюється в межах ![]() , тобто на верхньому розрізі
, тобто на верхньому розрізі ![]() а на нижньому розрізі
а на нижньому розрізі ![]() . Отже, дістаємо взаємно однозначну
відповідність: для кожної точки
. Отже, дістаємо взаємно однозначну
відповідність: для кожної точки ![]() Z відповідає лише одна точка
Z відповідає лише одна точка ![]() W.
W.
Моделювання за
допомогою комплексної функції (1) зводиться до того, щоб при певних заданих
значеннях аргументів ![]() Z отримати
очікувані оптимальні значення функціональних залежних величин
Z отримати
очікувані оптимальні значення функціональних залежних величин ![]() W та максимальне значення прибутку виробництва
W та максимальне значення прибутку виробництва ![]()
Дістаємо
обернену виробничу функцію:
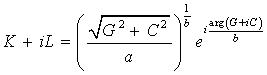 ,
,
або в тригонометричній формі:
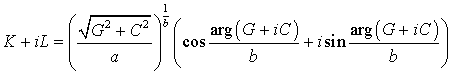 .
.
Звідси:
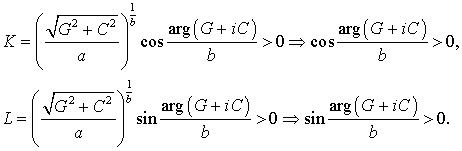
Звідси
![]() . (2)
. (2)
Отже, для очікуваних значень об’єктів К і L плануємо об’єкти G i C такими, що при збереженні
виробництва задовольняють умову (2) для отримання оптимального прибутку
виробництва.
Потрібно зауважити, що всі
складові комплексних змінних витрат виробництва і валового прибутку повинні бути приведені до одних і тих же одиниць виміру. Для цього можна
скористатися різними формулами нормалізації змінних, що приведе до їх
безрозмірності [1].
Література:
1.
Блудова Т.В., Мартиненко В.С. Теорія функцій комплексного
змінного. – К. Просвіта, 2000.-472 с.
2.
Светуньков И.С. Использование комплексных переменных в
теории производственных функций / Известия Санкт-Петербургского университета
экономики и финансов, 2007, № 4. С. 127-129.
3.
Светуньков С.Г., Светуньков И.С. Производственные функции
комплексных переменных: Экономико-математическое моделирование производственной
динамики. – М.: Изд-во ЛКИ, 2008. -136 с.