Економічні науки/ 8. Математичні методи в економіці

Скрильник І.І., Лупєкіна І.Є.

Полтавський національний технічний університет, Україна

Застосування імітаційного моделювання до управління запасами виробничих ресурсів

Сучасний науковий підпід до вивчення тих чи інших економічних об’єктів, процесів, функціонування систем вимагає застосування різних видів моделювання. Чимало науковців використовують імітаційне моделювання, яке дає можливість проводити дослідження у різних сферах економічної діяльності, наприклад: проектуванні та аналізі виробничих систем; аналізі фінансових та економічних систем; дослідженні систем масового обслуговування (СМО) та різних виробничих процесів. Відмінною особливістю імітаційного моделювання є дослідження на ЕОМ ситуацій, що імітують реальні процеси. Зокрема, для побудови імітаційної моделі функціонування складу авторами розглянуто задачу управління запасами виробничих ресурсів.

Постановка задачі. Нехай деяке підприємство відповідно договору щомісячно реалізує зі складу за домовленостями сировину для виготовлення продукції в обсязі 500 од., причому денний попит на неї є випадковою величиною і коливається від 10 до 20 од. Максимально можливе значення ймовірності зменшення запасу за день становить 16 од. Середні витрати на зберігання одиниці сировини складають 7 грн., а штраф за дефіцит (недопостачання) одиниці сировини дорівнює 9 грн. Побудувати імітаційну модель функціонування складу. Результати про кількість витрат та залишки сировини показати на дисплеї. Додатково вивести інформацію про вартість зберігання сировини та суму штрафів за вказаний період.

Математична модель. Виберемо за одиничний інтервал часу один місяць . Припустимо, що підприємство для виготовлення своєї продукції на період робить запас сировини в обсязі .

Нехай – це обсяг сировини, що необхідний споживачу (або споживачам) для виготовлення продукції за час (обсяг замовлень) при денному попиті , а – максимально можливе значення зменшення запасу за період . Якщо , то склад задовольняє заяву споживача, а залишки сировини

(1)

переносяться до наступного місяця , причому витрати на зберігання цього запасу пропорційні обсягу і дорівнюють

. (2)

Якщо обсяг замовлення , то склад віддає певний свій запас сировини, а за товар, який недопоставлено, несе витрати (наприклад, штрафується за дефіцит), які пропорційні дефіциту і дорівнюють:

. (3)

Таким чином, повні витрати складу можна записати у вигляді:

, (4)

при цьому залишок товару

. (5)

Отже, якщо:

, то

, то

, то

У класичній постановці задачі управління запасами передбачається, що сама величина денного попиту невідома, проте відомо, що вона є незалежно випадковою величиною, яка має заданий закон розподілу [1].

Повні витрати підприємства на зберігання ресурсів визначатимуться за формулою

. (6)

Чим меншими будуть витрати на зберігання та придбання ресурсів, тим нижчою буде собівартість продукції і вищою ефективність виробництва [1].

Параметри моделі:

– запас сировини 500 од.;

– щоденний попит на сировину для виготовлення продукції – випадкова величина, що має нормальний закон розподілу normrnd(10, 20);

– максимально можливе значення ймовірності зменшення запасу, при умові, що вказана денна величина становить 16 од.

– середні витрати зберігання одиниці сировини 7 грн.;

– штраф за дефіцит одиниці сировини 9 грн.;

– інтервал часу (30 днів).

Розв’язання задачі. Блок-схема імітаційної моделі представлена на рисунку 1.

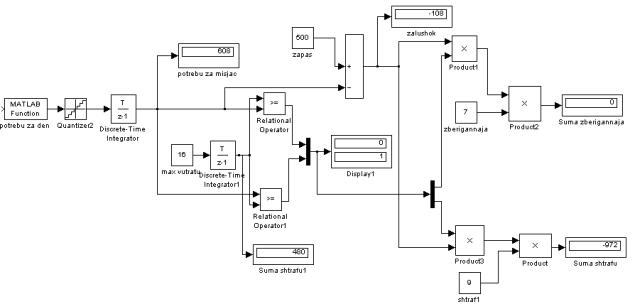
Рис. 1 – Імітаційна модель управління запасами виробничих ресурсів

При побудові даної S-моделі використаний блок MatLab Function, який імітує щоденний попит на сировину для виготовлення продукції. Даний блок є генератором випадкових величин, розподілених за нормальним законом normrnd(10, 20). Величину, отриману у результаті генерування, округлюємо до цілого значення за допомогою блоку Quanize. Щоб визначити попит на сировину за період часу , до вказаних вище блоків підключаємо блок Discrete Time Integrator. Максимально можливе значення ймовірності зменшення запасу представляємо за допомогою блоків Constant та Discrete Time Integrator. Визначений місячний попит на сировину та максимально можливе зменшення запасу сировини для підприємства порівнюємо за допомогою блоку Relational Operator. При цьому визначаємо або залишки сировини, або її дифіцит. Час моделювання функціонування складу налаштовуємо за допомогою команд: Simulation → Simulation parameters → Solver → Stop time = 30 [2].

У побудованій моделі розраховується вартість зберігання сировини та сума штрафу за період (рис. 2).

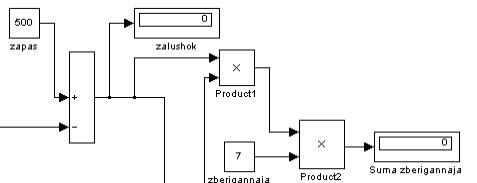
Рис. 2 – Розрахунок вартості зберігання сировини

Література:

1. Шаповалова О.О. Прикладні задачі моделювання економічних процесів. Ч.1: Навчальний посібник / О.О. Шаповалова, О.В. Старкова, А.В. Литвиненко. – Х.: ХДТУБА, 2010. – 164 с.

2. Гультяев А. Визуальное моделирование в среде MATLAB: Учебн. курс. / А. Гультяев – СПб: Питер, 2000. – 432 с.