К.т.н., доц. Беаз О.М., магістрант Лісовенко А.І.

Вінницький національний технічний університет, Україна

Математична модель процесу формування зовнішньої фрагментації динамічної пам’яті

Актуальність. Ефективність роботи алгоритмів розподілення динамічної пам’яті залежить від багатьох параметрів. Одним з головних параметрів є фрагментація пам’яті. Причиною цього є те, що фрагментація зменшує обсяг доступної пам’яті і крім цього збільшує час роботи алгоритмів. Дане явище виникає через те, що відсутня можливість доступу до вільних блоків пам’яті. Існує зовнішня та внутрішня фрагментація. Внутрішня фрагментація виникає через те, що певному додатку виділяється блок пам’яті, розмір якого більший, ніж було запитано (рисунок 1).

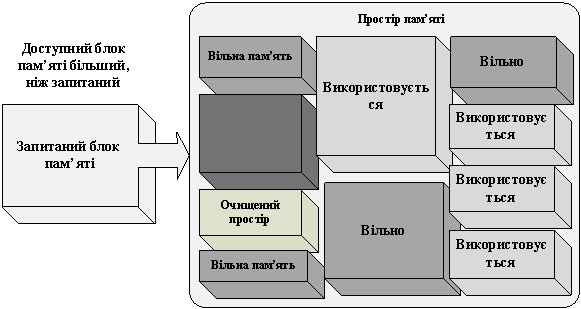
Рисунок 1 – Внутрішня фрагментація пам’яті

Зовнішня фрагментація виникає по причині наявності між вільними блоками пам’яті зайнятого блоку. Це призводить до того, що неможливо виділити суцільний блок пам’яті необхідного розміру, не зважаючи на те, що сукупний розмір вільних блоків має відповідний розмір (рисунок 2).

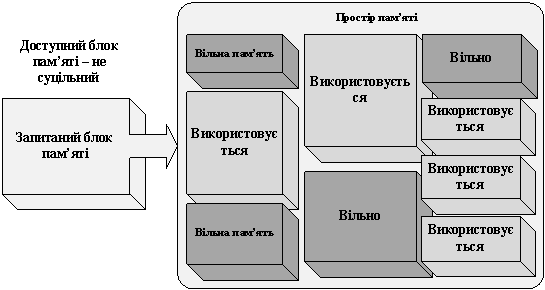
Рисунок 2 – Зовнішня фрагментація пам’яті

Явище фрагментації в цілому зменшує ефективність та продуктивність роботи всієї системи і тому необхідно шукати методи та способи її зменшення.

Для зменшення зовнішньої фрагментації необхідно проаналізувати чинники, від яких вона залежить та визначити математичні залежності, які нададуть можливість її оцінити.

В окремих роботах наведені математичні вирази та визначені залежності між фрагментацією та чинниками, які її формують [1,2,3]. В роботі [4] наведено вираз, який визначає кількісну оцінку явища фрагментації.

, (1)

де - розмір доступної динамічної пам’яті;

- розмір запитаного блоку пам’яті, який не може бути наданий.

Обґрунтування залежностей між чинниками, які формують фрагментацію та наведені в роботах [1,2,3] мають ймовірнісний та вибірковий характер. Так, в роботах [1,2], фрагментація оцінена за допомогою вибіркових та штучних умов, які виникають під час процесу виділення та звільнення блоків динамічної пам’яті. Ці умови сформовані на основі моделі роботи динамічної пам’яті, яка наведена в роботі [3]. Згідно цієї моделі, виділення та звільнення динамічної пам’яті, відбувається почергово, а сам стан комп’ютерної системи має прямувати до рівноваги. В реальних комп’ютерних системах, виділення та звільнення блоків динамічної пам’яті відбувається випадковим чином. Внаслідок цього, чинники та вирази наведені в роботах [1,2] повністю не відображають процеси виділення та звільнення блоків динамічної пам’яті. По цій причині не можливо повністю визначити чинники та залежності, які будуть впливати на розподіл динамічної пам’яті в реальній комп’ютерній системі. Метою даної роботи є формування математичної моделі, яка максимально відображає процеси, що відбуваються під час роботи алгоритму розподілу динамічної пам’яті та визначення на основі цієї моделі роботи динамічної пам’яті шляхів зменшення зовнішньої фрагментації.

Реалізація математичної моделі. Для формування математичної моделі необхідно проаналізувати процеси, які відбуваються під час розподілу динамічної пам’яті та стани структурних компонентів системи, які приймають участь у звільненні та виділенні динамічної пам’яті.

Нехай S – весь доступний обсяг динамічної пам’яті системи, який надається певному додатку. Цей доступний обсяг пам’яті може бути розподілений на блоки різного розміру і формувати певну конфігурацію цих блоків. Позначимо окрему конфігурацію розподілення динамічної пам’яті S_і. Кількість всіх можливих конфігурацій розподілення динамічної пам’яті – P формує простір конфігурацій. Згідно цього, весь простір динамічної пам’яті, який відповідає певній конфігурації, розподіляється на окремі блоки, де розмір окремого блоку пам’яті – s_і . Залежність між розподілом пам’яті, що відповідає певній конфігурації та розміром всіх блоків, що його утворюють, визначається виразом:

, (2)

де і – номер блоку динамічної пам’яті;

n – кількість блоків динамічної пам’яті в окремій конфігурації.

Нехай s_і – вільний блок динамічної пам’яті, а s_і’ – зайнятий блок динамічної пам’яті. В відповідності до цього, весь обсяг пам’яті Sі визначається виразом:

, (3)

де m – кількість всіх зайнятих блоків динамічної пам’яті;

k – кількість всіх вільних блоків динамічної пам’яті.

Під час роботи алгоритму динамічної пам’яті в певний проміжок часу окремі блоки можуть перебувати як в зайнятому, так і в вільному стані. Як було зазначено вище, зовнішня фрагментація відбувається в тому випадку, коли обсяг динамічної пам’яті, що запитує додаток буде більшим, ніж обсяг сукупної послідовності всіх вільних блоків між окремими зайнятими блоками (рисунок 1).

Обсяг V_i послідовності вільних блоків, які розташовані між окремими зайнятими блоками, визначається виразом:

. (4)

Сукупний обсяг вільної динамічної пам’яті визначається виразом:

, (5)

де l – кількість послідовностей блоків вільної динамічної пам’яті, які обмежені зайнятими блоками.

Виділення нового об’єму динамічної пам’яті окремому програмному додатку починається після того, як цей додаток сформував запит на виділення блоку динамічної пам’яті певного розміру. В залежності від обсягу динамічної пам’яті, який необхідний додатку, запит може бути різний. Обсяг певного блоку динамічної пам’яті, що має бути наданий додатку, позначимо req_і . Сукупність всіх можливих запитів req_і формує простір запитів Req req_і.

З аналізу виразу (1), фрагментація має визначатися мінімальним запитом req_і, який не може бути виконаний not_req_i. Очевидно, що найкритичніше значення фрагментації, має відповідати мінімальному обсягу запиту, під час якого вона виникає. Вираз 6:

, (6)

де – розмір послідовності вільних блоків, що має максимальне значення.

Математична модель, яка відображає виникнення зовнішньої фрагментації та поведінку блоків динамічної пам’яті при роботі комп’ютерної системи, визначається системою 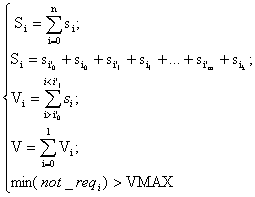7:

(7)

З аналізу системи 7 очевидно, що зовнішня фрагментація залежить від розміру послідовності вільних блоків, що має максимальне значення () та від мінімального запиту, який не може бути виконаний (not_req_i). Під час роботи, блоки динамічної пам’яті можуть бути в різних станах (вільний/зайнятий). У відповідності до цього, стан пам’яті z визначається сукупністю всіх блоків пам’яті, які є зайняті або вільні в даний момент часу. Зрозуміло, що кількість таких станів визначається виразом:

N_z = 2ⁿ. (8)

Фрагментація буде для кожного стану z залежати від послідовності вільних блоків динамічної пам’яті, обсяг кожної з яких – V_i.. Сукупність всіх послідовностей V_i для одного стану z певної конфігурації S_i формує масив {V_i}. Позначимо VMAX_z – максимальне значення масиву {V_i}. Для однієї конфігурації S_i, під час роботи комп’ютерної системи по причині перебування динамічної пам’яті в різних станах z параметр VMAX буде мати різне числове значення для кожного такого стану. Позначимо VMAX_{z_i} – максимальне значення, що відповідає певному стану динамічної пам’яті. Сукупність всіх можливих значень VMAX_z__i, яке відповідає певній конфігурації S_i і формується для кожного стану динамічної пам’яті z, створює масив {VMAX_{z_i}}. Позначимо VMAX_z__min – мінімальне значення цього масиву. Сукупність всіх значень VMAX_{z_min}, яка відповідає всім конфігураціям S_i, формує масив {VMAX_{z_min}}. Позначимо мінімальне значення зовнішньої фрагментації – Fmin, а конфігурація, яка їй відповідає – Smin_i. Зовнішня фрагментація Fmin конфігурації Smin_i, буде мати найменше числове значення серед інших конфігурацій S_i в тому випадку, якщо VMAX_z__min цієї конфігурації Smin_i, буде більше, ніж для значень VMAX_z__min всіх інших конфігурацій S_i.

Для того, щоб зменшити зовнішню фрагментацію, необхідно проаналізувати чинники, від яких залежить параметр VMAX_z__min. Як наведено вище, параметр VMAX_z__min визначений з простору всіх вільних послідовностей V_i кожного стану z для певної конфігурації S_i. Окрему вільну послідовність V_i утворюють вільні блоки s_i в динамічній пам’яті (вираз 4). З аналізу цього виразу зрозуміло, що послідовність V_i залежить від значень s_i та порядку їх розміщення в просторі пам’яті. Тому, фрагментацію можна зменшити шляхом визначення необхідного значення розміру блоків s_i та порядку розміщення цих блоків між собою. Для мінімальної зовнішньої фрагментації, значення розміру блоків s_i та порядку їх розміщення між собою, має задовольняти виразу:

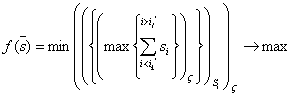. (9)

Одним з шляхів визначення розміру блоків s_i та їхнього порядку між собою в просторі динамічної пам’яті певного об’єму, які відповідають мінімальній фрагментації, можливо виконати двома кроками. Перший крок – програмне формування всіх можливих конфігурацій S_i динамічної пам’яті, всіх станів z, в яких може перебувати кожна конфігурація S_i. Другий крок – знаходження серед всіх сформованих конфігурацій S_i таких значень s_i та порядку їх між собою, які задовольняють виразу (9).

Висновки. В ході даного дослідження шляхом аналізу процесу, який має місце під час розподілу динамічної пам’яті комп’ютерної системи було сформовано математичну модель, яка відображає явище фрагментації динамічної пам’яті. Для зменшення числового значення зовнішньої фрагментації, в цій математичній моделі необхідно визначити такі параметри як розмір блоку та конфігурацію всього простору динамічної пам’яті (послідовність розміщення блоків різного розміру). Дані параметри мають бути визначені шляхом застосування певного методу оптимізації, це і буде напрямком подальших досліджень.

Література:

1. Denning P. J. Origin of Virtual Machines and Other Virtualities / P. J. Denning // AHC. – 2001. – Vol. 23. – № 3. – 73 р.

2. Denning P. J. Virtual Memory / P. J. Denning // Computing Serveys. – 1970, Vol. 2. – № 3 – P. 153 – 189.

3. Кнут Д. Е. Искусство программирования / Д. Е. Кнут // Т. 1. Основные алгоритмы. – М.: Вильмс, 2010 – 720 с.

4. S. Mamagkakis. Reducing Memory Fragmentation with Performance-optimized Dynamic Memory Allocators in Network Applications