Современные информационные технологии / 4. Информационная безопасность

Дьякова А.В., к.т.н., доц. Бойко А.А., к.т.н., доц. Яковлев Р.С.

Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е Жуковского и Ю.А. Гагарина» (г. Воронеж), Россия

Методический подход к оценке функциональной стабильности информационно-технических средств в условиях преднамеренных программных воздействий

Вопросы оценки функциональности и надёжности технических средств, работающих независимо от программного обеспечения, на сегодняшний день имеют достаточно глубоко проработанную теоретическую базу, применяя которую возможно существенно повысить качество этих средств в процессе их разработки и эксплуатации. В случае использования в техническом средстве программного обеспечения (далее – информационно-техническое средство или ИТС) возникает возможность для применения в отношении данного средства преднамеренных программных воздействий, способных снизить его функциональную стабильность (ФС). В таких условиях для обеспечения ФС необходимо стремиться к получению наиболее полной информации об имеющихся в ИТС уязвимостях для деструктивных специальных программных средств (СПС) и способах их устранения. Для решения этой задачи предлагается подход, позволяющий оценивать ФС ИТС с применением элементов теории игр. Выбор данного подхода обусловлен тем, что взаимодействие ИТС и СПС имеет характер ярко выраженного антагонистического конфликта [1]. При этом существует априорная неопределённость данных о потенциальных воздействиях СПС и возможной реакции ИТС на них.

Предлагаемая модель игровой обстановки соответствует матричной (двусторонней) игре с нулевой суммой, при которой выигрыш одной стороны равняется проигрышу другой (антагонистическая игра). Одна сторона моделирует СПС, реализующее преднамеренные воздействия, другая (средства обеспечения ФС, используемые в ИТС) – противодействует преднамеренным воздействиям, влияющими на ФС ИТС.

Моделирование осуществляется в два этапа.

Этап 1. Определение стратегий сторон.

Сторона А – СПС, имеет А_n стратегий (алгоритмов преднамеренных воздействий). Сторона В – средства обеспечения ФС ИТС, имеется В_m различных конфигураций (наборов). Требуется выбрать оптимальный набор средств обеспечения ФС из множества альтернатив при возможных стратегиях А_n СПС.

Определение множества потенциальных стратегий А_n СПС, применимых для конкретного вида ИТС, для которого в доступных источниках не найдено алгоритмов преднамеренных воздействий, способных повлиять на его ФС, предлагается осуществлять с помощью следующего алгоритма.

На шаге 1 осуществляется сбор информации об ИТС:

(1)

где N – количество элементов ИТС, потенциально подверженных преднамеренным воздействиям; i_n =1, когда информация об n-ом элементе ИТС найдена за интервал времени Δt, и i_n=0 – в противном случае.

В ходе шага 2 выявляются уязвимые для СПС места в ИТС:

(2)

где Tech_у – технология выявления уязвимых для воздействия мест в ИТС, G_n – количество уязвимых мест ИТС, выявленных в результате анализа информации об n-ом его элементе. Для формирования Tech_у предлагается использовать метод формальной верификации программного обеспечения MODEL CHECKING [2].

На шаге 3 для уязвимых мест в ИТС разрабатывается множество алгоритмов его реализации:

(3)

где Tech_по – технология разработки программного обеспечения, H_ng – количество алгоритмов, разработанных для реализации уязвимого места u_ng и реализованных в СПС.

Количество потенциальных стратегий А_n злоумышленника будет равняться количеству алгоритмов, разработанных для реализации уязвимых мест и реализованных в СПС: А_n=H_ng.

Этап 2. Выбор оптимального набора средств обеспечения ФС из множества альтернатив на основе матричных игр.

Поскольку количество возможных решений с обеих сторон конечно – соответственно для преднамеренных воздействий A ={A_i}, i =1, 2,..., N и набора средств обеспечения ФС В={B_j}, j =1, 2, ... , M, то значения платёжной функции F=F(A_i, B_j) представляются в виде матрицы F=||f_ij||, i = 1, 2, ... , N; j =1, 2, ... , M.

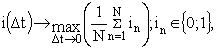
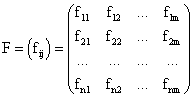	B1	B2	…	Bm
А1	f11	f12	…	f1m
А2	f21	f22	…	f2m
…	…	…	…	…
An	fn1	fn2	…	fnm

. (4)

В качестве платёжной функции будем использовать функцию ФС [3], характеризующую способность ИТС реализовать заданные функции (процессы формирования, создания, преобразования, использования и хранения информации) в условиях воздействия внешних и внутренних дестабилизирующих факторов. Следовательно, ФС можно представить в виде следующего отношения:

(5)

где и – количество задач, выполняемых ИТС при использовании набора средств обеспечения ФС B_j без преднамеренного воздействия A_i на него и с воздействием, соответственно. Следует отметить, что в общем случае в качестве платёжной функции может выступать также время противодействия преднамеренному воздействию, стоимость набора средств обеспечения ФС.

Выбор набора средств обеспечения ФС по принципу минимакса отвечает принципу гарантированного результата. Критерий максимина реализуется в виде , а минимакса – . Если игра имеет седловую точку, то есть , то данное значение будет являться гарантированным средним значением эффективности противодействия СПС. В случае отсутствия седловой точки решение необходимо искать в смешанных стратегиях, в общем виде матричная игра решается как задача линейного программирования симплексным методом.

Таким образом, предложен методический подход для оценки функциональной стабильности информационно-технических средств в условиях преднамеренных воздействий, который позволяет на основе теории матричных игр выбрать оптимальный набор средств обеспечения функциональной стабильности в условиях неопределённости преднамеренных воздействий.

Литература:

1. Климов С.М. Методы и модели противодействия компьютерным атакам. – Люберцы.: КАТАЛИТ, 2008. – 316 с.

2. Карпов Ю.Г. Model Checking. Верификация параллельных и распределенных программных систем – СПб.: БХВ-Петербург, 2010. – 551 с.

3. Симанков В.С., Сундеев П.В.. Системный анализ функциональной стабильности критичных информационных систем: Монография (научное издание) / Под науч. ред. В.С. Симанкова. Кубан. гос. технол. ун-т; Ин-т совр. технол. и экон. – Краснодар, 2004. – 204 с.