К. физ.-мат.н., Бырдин А.П., к. физ.-мат.н., Вислова Е.В., Лозовский В.А.

Воронежский государственный технический университет

ИТЕРАЦИОННЫЙ МЕТОД ДЛЯ ТРАНСФОРМАНТ РЕШЕНИЯ НЕЛИНЕЙНОГО ИНТЕГРОДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ В СВЕРТКАХ

Рассматривается метод решения нелинейных интегродифференциальных уравнений, возникающих в задачах динамики нелинейных наследственно-упругих сред. Метод основан на реккурентном итерационном процессе определения трансформант ядер интегрального ряда, представляющего решение.

Некоторые динамические задачи теории вязкоупругих сред с конститутивным уравнениями, содержащими нелинейные аналитические функционалы, сводятся к решению интегродифференциальных уравнений с нелинейными свертками. К подобным задачам относятся, например, задачи о распространении волн в нелинейно-наследственной среде [1], задачи о колебаниях осесимметрических конструкций, материал которых находится в плоском осесимметрическом деформированном состоянии [2], [3] и ряд других.

Возникающие в таких задачах дифференциальные уравнения имеют вид

, (1)

где для простоты взяты нулевые начальные условия,

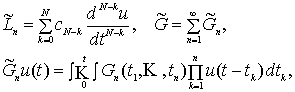(2)

− постоянные (), − заданные ядра наследственности, причем ядро первого порядка содержит аддитивную сингулярную составляющую в виде дельта-функции [4].

Решение задачи (1) будем искать в виде ряда Вольтерра

(3)

где операторы определены правилом (2). Ядра интегральных операторов подлежат определению. Отметим, что построение решений дифференциальных уравнений с использованием рядов Вольтерра осуществлялось в ряде работ, например, [5], [6]. Однако законченный алгоритм не был построен.

Выполнив преобразование Лапласа уравнения (1) и решения (3), получим:

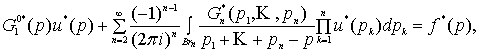(4)

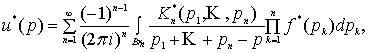(5)

где , , , − трансформанты Лапласа соответствующих функций, интегралы в формулах (4) и (5) вычисляются по n-мерному контуру Бромвича [7],

. (6)

Подставим трансформанту решения (5) в преобразованное по Лапласу уравнение (4). В результате получим уравнение, связывающее изображения искомых ядер в (3) с изображениями заданных ядер наследственности в уравнении (1). Имеем:

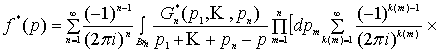
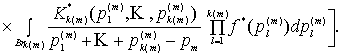(7)

Преобразуем произведение сумм в (7) к форме Коши, приравняем коэффициент линейного по члена в правой части равенства единице, а суммы интегралов с одинаковым числом произведений нулю. В результате получим систему алгебраических уравнений, определяющую лаплас-образы резольвентных ядер через трансформанты заданных ядер наследственности :

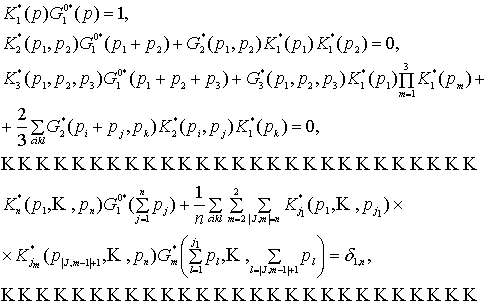(8)

Здесь − длина мультииндекса , , − символ Кронекера, внешняя симметризующая сумма берется по циклической перестановке индексов от 1 до n, что обусловлено требованием симметрии функций относительно перестановок аргументов. Внутренняя в последнем соотношении берется по натуральным решениям диофантова уравнения .

Система уравнений (8) имеет реккурентный характер и позволяет находить трансформанты искомых ядер , предварительно отыскав решения предшествующих уравнений. Отметим также, что эти соотношения являются взаимными в том смысле, что если за исходное принять соотношение (3), то трансформанты ядер определяются через лаплас-образы ядер из аналогичных соотношений.

Из соотношений (8) можно получить интегральные соотношения для ядер решения (3), переводя уравнения системы в пространство оригиналов с помощью обратного преобразования Лапласа. Первое из соотношений (8) определяет функцию , являющуюся резольвентой линейного интегродифференциального уравнения

,

где операторы определены в формулах (2).

Как правило, при описании экспериментальных результатов с помощью нелинейной теории наследственной упругости используют упрощенные физические уравнения [8]. В случае экспериментально наблюдаемого подобия кривых, полученных в опытах на релаксацию напряжений в материале, определяющее соотношение, связывающее напряжения с деформациями нелинейным функционалом, будет содержать кратноинтегральные выражения с сепарабельными ядрами наследственности

(9)

где параметры сепарабельности находятся из опыта.

В этом случае решение уравнения (1), ядра наследственности в котором являются сепарабельными функциями (9), будет также выражаться формулой (3). Реккурентное соотношение для трансформант ядер интегралов в (3), полученное из соотношений (8), будет иметь вид

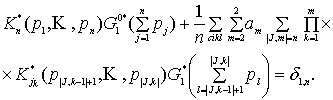
В частном случае, когда в уравнении (1) отсутствует дифференциальный оператор, решение (3) будет содержать ядра, трансформанты которых определены равенствами:

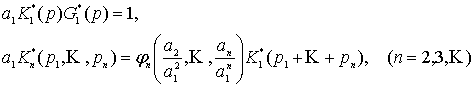(10)

Функцию в соотношениях (10) в некоторых случаях можно построить в явном виде. В частности, при можно получить зависимость . В другом частном случае, при зависимость этой функции от номера имеет более сложный характер

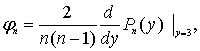
где − полиномы Лежандра порядка n.

Рассмотренный здесь метод решения интегродифференциальных уравнений можно применять и для построения решений дифференциальных уравнений, содержащих степенную нелинейность. Это связано с тем, что такие дифференциальные уравнения можно представить в виде интегродифференциальных с сепарабельными ядрами, выражающимися через дельта-функции.

Литература:

1. Бырдин А.П., Розовский М.И. О волнах деформации в нелинейной наследственно-упругой среде. Изв. АН СССР, МТТ, 1984, №4. С. 100-104.

2. Москвитин В.В. Сопротивление вязко-упругих материалов применительно к зарядам ракетных двигателей на твердом топливе. М.: Наука, 1972. – 328 с.

3. Победря Б.Е. О решении задач термо-вязко-упругости с неоднородным полем температур. Упругость и неупругость. М.: МГУ, 1971, Вып. 1. С. 172-201.

4. Быков Д.Л., Ильюшин А.А., Огибалов П.М., Победря Б.Е. Некоторые основные проблемы теории термо-вязко-упругости. Механика полимеров, 1971, №1. С. 41-58.

5. Нелинейные электромагнитные волны. М.: Мир, 1983. – 312 с.

6. Богданович В.М., Черкас Л.А. и др. Методы нелинейных функционалов в теории электрической связи. – М.: Радио и связь, 1990. – 280 с.

7. Диткин В.А., Прудников А.П. Операционное исчисление. – М.: Высшая школа, 1975. – 407 с.

8. Работков Ю.Н. Элементы наследственной механики твердых тел. – М.: Наука, 1977. – 384 с.