Математика/1.Дифференциальные и интегральные уравнения

К.ф.-м.н., доцент Батыров Б.Е., Мурзатаева Э.С.

Северо-Казахстанский Государственный университет им.М.Козыбаева

Об одном применении модели Ферхюльста

В природе и обществе встречаются многочисленные процессы, в ходе которых некоторые величины изменяются по следующему закону: в течение любого промежутка времени фиксированной длительности значение величины меняется в одно и то же число раз.

Аналогично обстоят дела в любой совокупности живых существ при условий, что нет ограничений в пище и в пространстве и нет истребляющих их врагов. Известны случаи, когда некоторые виды животных и растений, попав в благоприятные условия, размножались столь быстро, что становились бедствием (саранча в Африке, кролики в Австралии, водяной гиацинт в США и т.д.).

Процессы, в которых величина увеличивается за равные промежутки времени в одно и то же число раз, называются процессами естественного роста.

Если допустить, что значение величины меняется в одно и то же число раз в течение промежутка фиксированной длительности , а мгновенно, то мы приходим к процессу, при котором скорость изменения величины в момент времени пропорциональна значению этой величины в тот же момент времени. Уравнение, описывающее этот процесс, можно записать так:

Так как , то получим дифференциальное уравнение с разделяющимися переменными:

(1)

Дифференциальное уравнение (1) было предложено Мальтусом в 1798 г. для прогнозирования роста населения Земли. Постоянная социальных и биологических науках именуется мальтузианским коэффициентом линейного роста.

В соответствии с законом Мальтуса численность населения должна расти экспоненциально, что не всегда справедливо, ибо не согласуется с реальностью. Дифференциальное уравнение (1), разумеется, слишком упрощенно изображает реальную ситуацию, и его решение далеко от истинного течения процесса. При использовании моделей естественного роста в социальных науках надо иметь в виду, что темпы роста, описываемые первоначально экспоненциальной функцией, в дальнейшем замедляются, наступает период насыщения.

Для преодоления противоречия с реальностью, необходимо принять во внимание эти факторы и соответствующим образом модифицировать модель роста.

Дж. Кьютелет предположил, что k в уравнении (1) должна быть не постоянной, а убывающей функцией, зависящей от y(t):

(2)

На основании этого в 1836 г. его ученик Ферхюльст предложил использовать для роста населения уравнение

(3)

т.е. считать, что

(4)

Модель Ферхюльста применяется и к другим социально-экономическим явлениям. Рассмотрим ее применение в сфере экономического роста в Республике Казахстан. Найти закон роста урожайности зерна в условиях конкуренции и насыщаемости рынка.

По условию задачи, происходит насыщаемость рынка. Согласно Ферхюльсту величина в условиях насыщаемости удовлетворяет дифференциальному уравнению (3). Поэтому рост продукции y(t) в условиях насыщаемости рынка будет также описываться уравнением Ферхюльста и соответствующее решение выражаться формулой (4) [1].

Массовое производство пшеницы в Казахстане берет начало с 1954 года, когда была начата программа по освоению целинных и залежных земель. За шесть лет (1954-1960) в Казахстане было введено в действие 25,5 млн.га пашни или 61% от всех вспаханных целинных и залежных земель по бывшему СССР.

Исторический максимум валового сбора пшеницы наблюдался в 1956 году - 19,2 млн. тонн. К 1999 г. посевная площадь пшеницы снизилась более чем в два раза, до почти 9 млн. га. Кроме других факторов, относящихся к состоянию экономики и сельского хозяйства, причиной резкого падения (-15% по сравнению с 1998 г.) послужила засуха 1998 года, когда был собран рекордно низкий урожай пшеницы - 4,75 млн. тонн. Начиная с 2000 года, посевная площадь пшеницы росла практически непрерывно и достигла 14,8 млн. га, 22 млн тонн в 2009 году, 26 млн. тонн в 2011 и 14 млн. тонн в 2012 году[2]. И в 2013 году по прогнозам ожидается 14 млн. тонн зерна в связи с засушливой погодой.

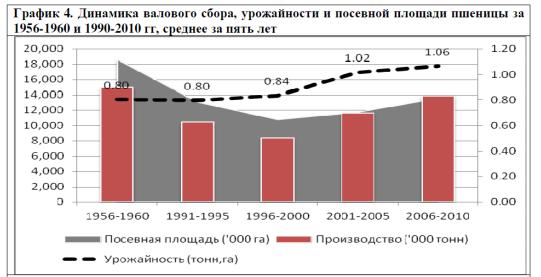
Таким образом, можно сказать что характер роста меняется, темпы роста замедлются.

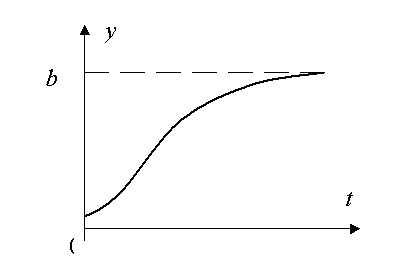
При кривая асимптотически приближается к прямой y=b. Значит, объем выпускаемой продукции в единицу времени стремится к конечному значению b.

Исходя из всего этого, можно сказать, что логистический рост более точно описывает развитие экономики.

Литература:

1. Ахтямов А.М. Математика для социологов и экономистов: Учеб. пособие. - М.:ФИЗМАТЛИТ,2004.- 464 с.

2. Ошакбаев Р.С. Перспективы и анализ экспорта пшеницы, 2012.-45с.