К. ф.-м. н. Е.И. Мирская,

А.К. Дмитриев

Брестский государственный университет имени А.С. Пушкина,

Республика Беларусь

ИССЛЕДОВАНИЕ ОДНОЙ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА

Спектральный анализ временных рядов является одним из основных направлений в исследованиях ученых многих стран мира, причем особое внимание уделяется методам спектрального анализа стационарных случайных процессов. Методы спектрального анализа можно разбить на две основные группы: методы, основанные на применении преобразования Фурье и методы линейного моделирования. Объектом исследования первой группы (непараметрические методы) является спектральная плотность случайного процесса.

Среди непараметрических методов спектрального оценивания одним из наиболее распространенных является метод Уэлча [1]. Этот метод предполагает деление временного ряда на интервалы и вычисление периодограммы для каждого из них. Итоговая оценка получается путем осреднения отдельных периодограмм. Введение такой процедуры осреднения позволяет уменьшить дисперсию оценки в число раз, равное числу интервалов разбиения.

Важным является применение специальных функций – окон просмотра данных, применение которых позволяет управлять эффектами, обусловленными наличием боковых лепестков в спектральных оценках.

Уэлч предложил использовать окно просмотра данных Ханна и 50%- ное перекрытие интервалов наблюдений.

Рассмотрим действительный стационарный случайный процесс , с , неизвестной взаимной спектральной плотностью

Пусть – последовательных наблюдений, полученных через равные промежутки, за составляющей процесса .

Предполагаем, что число наблюдений представимо в виде , где – число пересекающихся интервалов, содержащих по наблюдений, а принимает целочисленные значения, .

Используя методику Бриллинджера Д. [2], в качестве оценки взаимной спектральной плотности исследована статистика вида

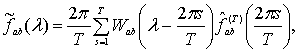(1)

где – спектральное окно, а , – оценка взаимной спектральной плотности процесса , построенная по методу Уэлча

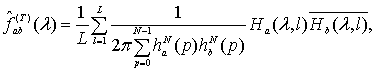(2)

где задано выражением

(3)

, причем наблюдения сглаживаются одним и тем же окном просмотра данных

В данной работе исследована скорость сходимости математического ожидания оценки , предполагая, что , , удовлетворяет условию

, (4)

для любых , – некоторая положительная постоянная,

Предположение 1. Пусть окна просмотра данных ограничены единицей и имеют ограниченную постоянной вариацию.

Предположение 2. Пусть непрерывная, периодическая функция с периодом , имеет ограниченную вариацию и является ядром.

Лемма 1. Для ядра , , при любом

(5)

Теорема 1. Если взаимная спектральная плотность непрерывна в точке и ограничена на , окна просмотра данных удовлетворяют предположению 1, а спектральные окна предположению 2, то для оценки , заданной выражением (1), справедливо соотношение

(6)

Теорема 2. Если взаимная спектральная плотность , , , удовлетворяет соотношению (4), то для математического ожидания оценки , , задаваемой (1), имеет место равенство

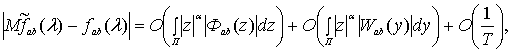
где

Доказательство. Учитывая, что математическое ожидание оценки имеет вид

,

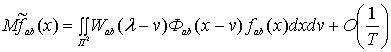используя соотношения (4) и (5), получим требуемый результат. Теорема доказана.

Литература:

1. Welch, P. D. The use of FFT for the estimation of power spectra / P.D.Welch // IEEE Trans. Electroacoust. – 1967. – V. 15, № 2. – Р. 70–73.

2. Бриллинджер, Д. Временные ряды. Обработка данных и теория. - М.:Мир, 1980. - 536 с.

3.Труш, Н.Н. Асимптотические методы статистического анализа временных рядов / Н.Н. Труш. – Мн.: БГУ, 1999. – 218 с.