Ìàòåìàòèêà / 5. Ìàòåìàòè÷åñêîå
ìîäåëèðîâàíèå
Ivanov Y.Y.
Vinnytsia National Technical University, Ukraine
Expansion for the Mathematical
Apparatus of the Algebra
Logarithm of the Likelihood Function
for the Turbo-Codes in Distributed
Computer Systems of Different Functional Purposes
Introduction. At the time of the latest
technology the information became object of the automated processing. The data
transfer process in information systems is susceptible to errors, because any
error in material breach of the calculation. To combat interferences in data transfer systems at all the stages
is used the error-correction coding, that provides reliability and credibility
of information transmitted. The analysis of the methods allowed us to determine,
that the most prominent achievement in the
theory of error-correction coding in recent years is turbo-code. They are used
to encode large volume information messages at the high speed with high
error-correcting [1]. Turbo-codes are used in practice in the most important
areas, such as space satellite communications (standards DVB-S, DVB-RCS),
digital television (ViaSat, HDTV), mobile communication systems of the 3rd
generation [2]. The practical widespread have decoding algorithms: SOVA (Soft-Output
Viterbi Algorithm), MAP (decoding algorithm for the Maximum A posteriori Probability)
and modifications to decrease the computational complexity (Log-MAP, Max-Log-MAP) [3].
A significant
drawback of the turbo-codes is comparatively
high decoding complexity and high delay, which sometimes make them
unattractive. But for using in satellite channels this shortcoming is not
essential, because the length of the communication channel introduces a
significant delay. Another
drawback of the turbo-codes (fig. 1) is a comparatively
small code distance. This leads to the fact, that even when a large input error
probability, the turbo-code performance is high, but at the low input error
probability the turbo-code performance is limited [1].
An important advantage of the turbo-codes is the decoding complexity independence from the length of the information block, which reduces the decoding error probability by increasing its length
[1].
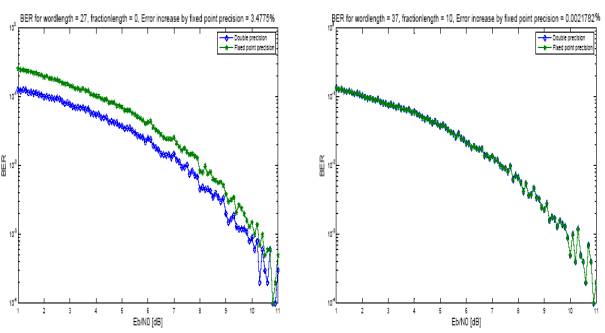
Figure
1 − BER − Bit Error Rate (word length 27 bits and 37 bits)
The main problems are the lack of freeware
distribution and complexity of the decoding algorithms.
The work purpose is to improve computing
efficiency of the turbo-code decoding procedure
through improvement of the mathematical algorithms of
their work.
Main Part. To achieve the purpose should be
to build a model of error-corection turbo-decoder, that uses the new
mathematical principles of the algebra logarithm of the likelihood function [4]
for N statistically independent
information bits with the transition to trigonometric and hyperbolic
functions without using complex numbers.
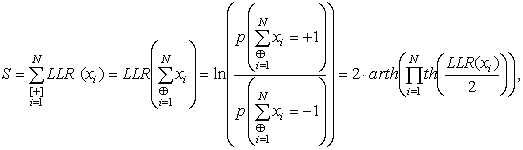 (1)
(1)
where ![]() − statistically independent
information bit,
− statistically independent
information bit, ![]() .
.
Equation (1)
can be used to simplify calculations, when solving complex problems, when given
a lot of statistically independent information bits. For the given formula is
possible to perform a connection between trigonometric (L. Euler, F. Viete, N.
Copernicus, Arabic mathematics) and hyperbolic (A.
de Moivre, V. Riccati, J.H. Lambert) functions without using complex numbers (C. Gudermann function) [5, 6] to simplify the
calculation.
Therefore, it
is necessary to find Gudermannian [5] from some argument ![]() .
.
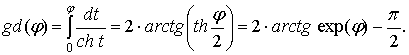 (2)
(2)
Now we use
the transformation
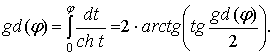 (3)
(3)
Comparing
formulas (2) and (3), we can obtain such Gudermannian property
![]() (4)
(4)
Applying this property to the expression (1), and using the Gudermannian form (2),
it is possible to obtain
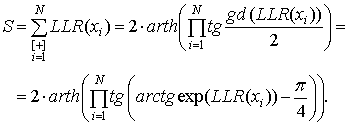 (5)
(5)
Now it is necessary to perform numeric calculations in the environment
of the mathematical modeling MathCad (fig. 2) to calculate the values sum of
the logarithm of the likelihood function for example in the case of 2 and 6 statistically independent information bits.

Figure
2 − Calculations (![]() bits)
bits)
Conclusion. So, has been derived a new formula for
calculating the LLR sum S for many bits. It can be used in computing
devices, for optimizing the approximation in distributed
computer systems of different functional purposes.
Literature:
1.
Êóëèê À.ß. Äåêîäóâàííÿ òà ðåàë³çàö³ÿ àëãîðèòìó BCJR äëÿ òóðáî-êîäó ñòàíäàðòèçîâàíîãî
â DVB-RCS / À.ß. Êóëèê, Ä.Ñ. Êðèâîãóá÷åíêî, Þ.Þ. ²âàíîâ // ³ñíèê Ñóìñüêîãî
äåðæàâíîãî óí³âåðñèòåòó. Ñåð³ÿ: Òåõí³÷í³ íàóêè. − Ñóìè: ÑÓÌÄÓ, 2012.
− Ò. 4. − ¹ 1. − Ñ. 84-93.
2.
Sripimanwat K. Turbo-Code Applications: A Journey from a Paper to Realization / K. Sripimanwat. − New-York:
Springer, 2005. − 386 p.
3.
Morelos-Zaragoza R. The Art of Error-Correcting Coding, 2nd Edition / R. Morelos-Zaragoza. − Chippenham: John
Wiley & Sons, Ltd, 2006. − 278 p.
4.
Moon T.K. Error-Correction Coding: Mathematical Methods and Algorithms /
T.K. Moon. − John Wiley & Sons, Ltd, 2005. − 750 p.
5.
Ãðàäøòåéí È.Ñ. Òàáëèöû èíòåãðàëîâ, ñóìì, ðÿäîâ è ïðîèçâåäåíèé (4-å èçä.) / È.Ñ.
Ãðàäøòåéí, È.Ì. Ðûæèê. − Ì.: Íàóêà, 1963. − 1100 ñ.
6.
Êîðí
Ã.À. Ñïðàâî÷íèê ïî ìàòåìàòèêå äëÿ íàó÷íûõ
ðàáîòíèêîâ è èíæåíåðîâ (4-å èçä.) / Ã.À. Êîðí, Ò.Ì. Êîðí. − Ì.: Íàóêà, 1978. − 832 ñ.