Математика/Математическое
моделирование
Ляпунова Ирина Артуровна
Южный
федеральный университет в г. Таганрог, Россия
Об одной
демогенетической модели динамики насекомых
Как известно,
особи изменяют свою скорость, в зависимости от качества и близости кормового
пятна. В частности, в моделях сообщества хищник-жертва ускорение движения
хищника определяется неоднородностью распределения плотности жертв [1]. Тем не менее, в современных демогенетических
моделях влияние популяционного таксиса не отражается [2].
Рассмотрим
распределение заданной агрокультуры на некотором одномерном физическом пространстве Ω. Пусть R=R(x,t) – прирост биомассы кукурузы; ![]() – мальтузианский коэффициент прироста. Уравнение динамики плотности биомассы:
– мальтузианский коэффициент прироста. Уравнение динамики плотности биомассы:
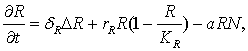 (1)
(1)
![]()
Здесь g(x,y,t) – функция,
учитывающая плодородие конкретного участка.
Демогенетические модели предполагают
наличие двух видов растительных ресурсов – обычного и трансгенного:
![]() , (2)
, (2)
где ![]() - начальная
биомасса растительного ресурса обычного вида,
- начальная
биомасса растительного ресурса обычного вида, ![]() - начальная
биомасса растительного ресурса трансгенного вида.
- начальная
биомасса растительного ресурса трансгенного вида.
Тогда прирост биомассы для обоих
видов растений c учетом
диффузии [4] осуществляется по формулам:
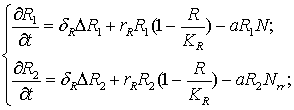 (3)
(3)
Введем функции, распределенные
согласно закону Менделя; ![]() - плотность
генотипа ij в точке
- плотность
генотипа ij в точке ![]() в момент времени t (
в момент времени t (![]() или s),
или s), ![]() ,
, ![]() ,
, ![]() – плотности
соответствующих генотипов вредителя [2,3].
– плотности
соответствующих генотипов вредителя [2,3].
![]() (4)
(4)
- общая
плотность популяции.
Активность вредителей определяется суммой
плотностей двух видов насекомых - вредителей:
![]() , (5)
, (5)
где ![]() и
и ![]() - плотности вредителей в активном и пассивном состоянии
соответственно.
- плотности вредителей в активном и пассивном состоянии
соответственно.
В активном состоянии, учитывая, что вредитель, неустойчивый к яду,
поедает только не трансгенную агрокультуру, получаем следующую систему
уравнений (6):
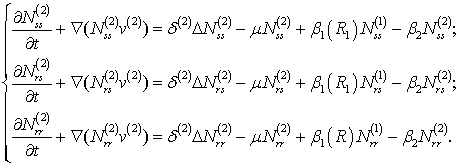 (6)
(6)
Медленный таксис в пассивном
состоянии для трех видов насекомых - вредителей описывается следующими
уравнениями (7):
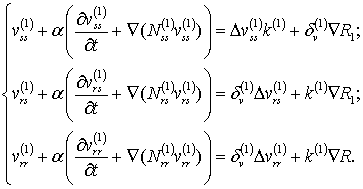 (7)
(7)
Быстрый таксис в активном состоянии
описывается одним уравнением для насекомых-вредителей, устойчивых к яду (8):
![]() (8)
(8)
Во всех случаях границы области
предполагаем непроницаемыми:
![]()
![]()
![]() .
.
Литература
1. Жадановская E.A.,
Тютюнов Ю.В., Ардити Р. Моделирование стратегии “высокая доза – убежище” при
использовании генетически модифицированной кукурузы для подавления кукурузного
стеблевого мотылька // Известия ВУЗов, Северо-Кавказский регион. Естественные
науки, 2006. - Приложение, №11. - 5 с.
2. Кажарова
И.А. Мозаичная
структура распределенного сообщества трансгенной кукурузы// Известия Южного федерального
университета. Технические науки. 2009. Т. 97. № 8.
С. 148-155.
3. Ляпунова
И.А. Устойчивость
модели пространственного распределения кукурузы вследствие процессов
запаздывания// Известия Южного федерального
университета. Технические науки. 2010. Т. 107. № 6.
С. 126-131.
4. Сухинов
А.И., Никитина А.В. Математическое моделирование и экспедиционные исследования
качества вод в Азовском море//Известия ЮФУ. Технические науки. -2011. -№ 8
(121). -С. 62-73.