ДЕКОМПОЗИЦИЯ УРАВНЕНИЙ ДВИЖЕНИЯ

¹Будылина Е.А., ²Гарькина И.А., ²Данилов А.М.

¹Московский государственный машиностроительный университет

²Пензенский государственный университет архитектуры и строительства

Ограничимся системами четвертого порядка (например, продольное или боковое движения летательного аппарата). При известных коэффициентах характеристического полинома задача сводится к определению корней уравнения:

.

Справедливы приводимые ниже утверждения.

1. Для того, чтобы движение содержало две колебательных составляющих (например, фугоидное и короткопериодическое), достаточно выполнения одного из следующих условий:

1.1. ;

1.2. ;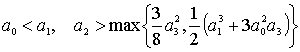

1.3. ;

- действительные корни многочлена ;

1.4. ;

где - действительный корень многочлена .

2. Для апериодичности движения (все корни - действительные) достаточно выполнения условий

;

().

3. Для того, чтобы движение содержало лишь одну колебательную составляющую, достаточно выполнения одного из условий

3.1. .

3.2. .

4. Приближенное условие устойчивости длиннопериодического движения:

.

5. Справедливы приводимые ниже соотношения для определения корней многочлена в зависимости от его коэффициентов.

5.1. Если и одновременно, то корни многочлена есть

;

5.2. Если , то

,

где - корни многочлена третьей степени .

5.3. Если , то

,

где

,

,

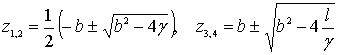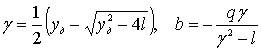- больший по модулю действительный корень многочлена

.

6. При определении корней многочлена можно воспользоваться приводимыми ниже утверждениями.

6.1. Если ; , то для корней справедливо:

,

где

, , .

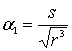6.2. Если , то

.

где

,

,

.

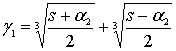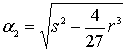Полученные результаты использовались при разработке концепции и создании имитаторов транспортных систем, в том числе модульной архитектуры [1], с требуемыми характеристиками.

Литература

1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э.В., д.т.н., профессора Данилова А.М. – Пенза, ИИЦ ПГУ, 2005. – 146 с.