Mathematics/5. mathematical modeling
Doctor of physical and mathematical
sciences Solovjov S.
Pacific National
University, Khabarovsk, Russia
Modeling immersing of lithosphere
plate in mantle
Results of numerical modeling of the convective heat exchange in the
mantle are shown. Subduction zone is considered where collision of the moving lithosphere
plate with the overriding continental plate occurred with subsequent subsidence
of the oceanic plate along the trench which axis lies at an angle j to the land
surface. As a result of numerical solution of the problem, using the Patankar’s
control-volume-method, the fields of temperature, stream function, vortex,
local Nusselt number at the upper and lower border of
calculating area were received. The gravitational acceleration changed under the linear law.
Mantle convection is a
principal driving mechanism of geological and geophysical phenomena we observe
on the Earth. Many researchers of the mantle dynamics concentrate their effort
on developing physical models using numerical simulation as a powerful tool to
understand the dynamics of mantle convection. We have developed simulation to
study dynamics of the Earth's mantle. The difficulties which the Earth
scientists are faced, by all accounts, are caused by two reasons:
- difficulty to
penetrate into the Earth's interior;
- loss of colossal
information on the evolution of the Earth.
In spite of a great number of publications dealing
with a study of the natural mantle convection, the questions concerning the
character, structure and the primary reason for occurrence of the convection
remain still open. In fact, the influence of convection on the geometry of
plates and, also, differences in the character of convection caused by using
the Newtonian and non-Newtonian models of Earth’s mantle, has not been studied
yet. The paper considers model of the continuous convection of the lithosphere
plate close to oceanic trench with regard for the heat of the phase transition.
The subduction zone is considered, where lithosphere plate collides with continental, and then on a trough,
which axis is located under an angle j to the
land surface, is immersed in mantle. The depth of immersing of lithosphere plate in mantle is determined as a result of the task
decision. It is accepted, that the gravitational acceleration on mantle depth varies under the linear law g = Àó + Â.
Constructing the mathematical
model, the following assumptions have been adopted: the lithosphere plate and
the underlying mantle are considered as the non-compressible Newtonian liquid
with a very high viscosity. The temperature at a boundary between the mantle
and the plate is constant and equals to the temperature of solid state Ts. The thermal conductivityl, the viscosity of
the substance m and the heat flux qv are determined with
account of their temperature dependence:
1. 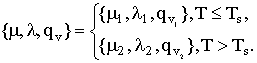
Index 1 denotes the lithosphere parameters, 2 -
the mantle parameters. The dependence of the density p on the temperature of
the medium is assumed to be
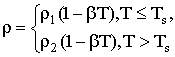
2.
Border between lithosphere and mantle is isotherm of solid
phase with value of temperature Ts.
3. The relative quantity of the solid phase g (characterizing melting and crystallization of the substance) contained
in the mantle or lithosphere is determined depending on the state of the
substance (a solid state with a temperature TS or a liquid state
with a temperature TL). The relative
quantity of the solid phase g,
depending of temperature, approximates by cubic spline:
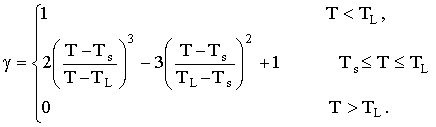
At g < 0.95 it is
assumed that the substance is in the melted (liquid) state, while at g > 0.95 - in the solid state.
Fig. 1 shows physical setting of a problem. The
horizontal oceanic plate moves towards the continental plate with a constant
velocity U0, and subsides in the
asthenosphere in the trench zone at an angle j to the land surface
with the same velocity. In turn, the continental plate moves towards the
oceanic plate with a velocity Uk.
Most often the lithosphere plates are subsiding in the subduction zones at an
angle of 45°, though in some sectors of the island arcs the angles of
subsidence from 30° to 90° have been marked. Here Uk
- velocity of a continental plate, U0 - velocity of oceanic (lithosphere) plate;
index 1 – lithosphere parameters, 2 – mantle parameters; j - angle
of immersing of oceanic plate; Ã1, Ã2, Ã3 - right, lower and left border of a trench, on which the plate is immersed, accordingly.
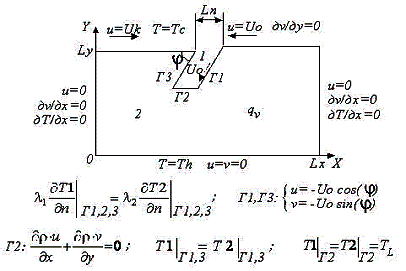
Fig. 1. Physical statement of a task
Location
of trough, on which the plate is immersed, is considered equal Lx /2. The lower
border Ã2, up to
which the velocity of immersing of a plate is known, is determined on the
interval of temperature melting. At achievement of melting temperature (liquid) TL the lithosphere plate melts and depth of its immersing in mantle is determined.
The mathematical statement of a task
describing convection in subduction zone includes the equations of movement of
an incompressible liquid in the Boussinesq approximation, continuity and energy with account internal heat sources. The
governing dimensionless equations can be written as:
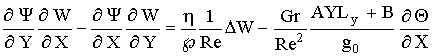 ,
,
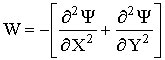 ,
,
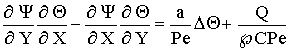 .
.
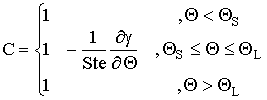 .
.
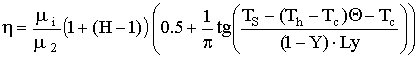 ,
,
H = [0;1] - the dimensionless
mantle depth.
Boundary
conditions:
![]() = 0 at Y = 1;
= 0 at Y = 1; ![]() = 1 at Y = 0;
= 1 at Y = 0; ![]() at X = 0 and X
= Lx/Ly.
at X = 0 and X
= Lx/Ly.
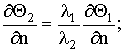
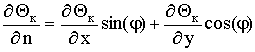 , (k = 1,2,3) at border Ã1, Ã2, Ã3 (fig.
1).
, (k = 1,2,3) at border Ã1, Ã2, Ã3 (fig.
1).
Q1 = Q2 at
border Ã1, Ã3; Q1 = Q2 = QL at
border Ã2.
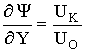 at X = [0;
(Lx/2Ly - Lp/2Ly)]; Y = 1.
at X = [0;
(Lx/2Ly - Lp/2Ly)]; Y = 1.
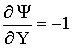 at X =
[(Lx/2Ly - Lp/2Ly); Lx/Ly]; Y = 1.
at X =
[(Lx/2Ly - Lp/2Ly); Lx/Ly]; Y = 1.
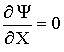 ,
, 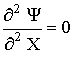 at X = [0;
Lx/Ly];
at X = [0;
Lx/Ly]; 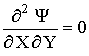 at
at![]() ;
; ![]() at Y = 0.
at Y = 0.
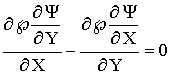 at
at ![]() (fig. 1).
(fig. 1).
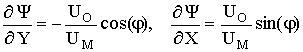 at Ã1, Ã3 (fig. 1) and inside a trench.
at Ã1, Ã3 (fig. 1) and inside a trench.
For
intensity of a vortex W the boundary conditions were calculated with the use of
boundary conditions for stream function. In accounts the non-uniform grid with
a condensation in trench region and at the upper boundary of the
area (Y = 1) was applied. Dimensionless
local Nusselt numbers on top (Y=1) and bottom (Y=0) border of calculated area
were determined by the expression ![]() (the derivative was calculated
on three points with the second order of approximation).
(the derivative was calculated
on three points with the second order of approximation).
The values of temperature at upper and lower border
are accepted equal ![]() K,
K, ![]() K. The extent of area on an axis õ is accepted equal 3000 km, and on
an axis y - 1000 km. Lithosphere thickness Ln -
100 km. The Temperatures of solid state Ts and
liquid state
TL are 1800Ê and
1900Ê accordingly. Velocity
of movement of a continental plate Uê = 1 ñm/year,
and velocity of oceanic plate U0 changed in an interval 1 - 9 ñm/year.
K. The extent of area on an axis õ is accepted equal 3000 km, and on
an axis y - 1000 km. Lithosphere thickness Ln -
100 km. The Temperatures of solid state Ts and
liquid state
TL are 1800Ê and
1900Ê accordingly. Velocity
of movement of a continental plate Uê = 1 ñm/year,
and velocity of oceanic plate U0 changed in an interval 1 - 9 ñm/year.
On fig. 2 the results of calculation for velocity of
movement oceanic plate 1 ñm/year and angle of a feat under
continental plate 30o are submitted. Re=1,05×10-19; Gr
= 3,2×10-14; Pe = 251; Ste = 3.Gravitational acceleration
value g = 9,8 is constant.
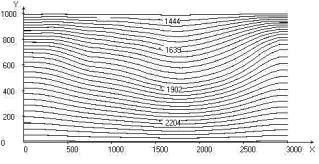
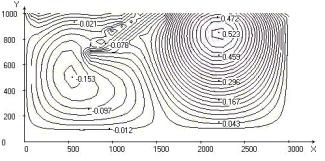
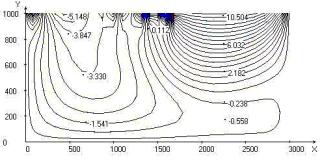
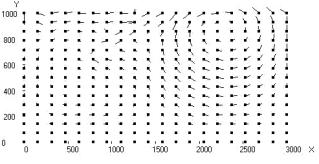
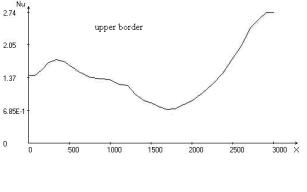
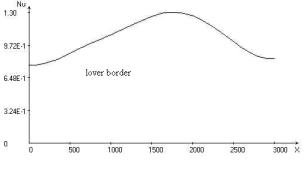
Fig. 2.
Calculated fields for j = 30o,
Uo = 1: temperature; stream function; vortex intensity; velocity vector field;
Nusselt number distribution on upper and lower border of the area
In trench region isothermals "bend" to lower boundary of the area (fig. 2).
Under oceanic and continental plates two
large-scale convective cells are formed, the liquid in which is gone in
opposite directions. And besides convective cell and vortex under continental
plate flow round immersed lithosphere and
penetrate into area of oceanic convective cell
and vortex, located to the right of subduction zone, moving them to the right.
The depth of immersing lithosphere achieves
value approximately 300 km. The distributions of Nusselt numbers on the upper
and lower boundaries of the area are given. At value x ~ 1700 km (fig.
2) in the collision region of plates takes place minimum heat flow on the upper
border of calculated area that will be agreed with known experimental data. On fig. 3 the results for velocity of movement oceanic plate U0 = 5 ñm/year are given. The depth of
immersing achieves value approximately 400 km. Oceanic convective cell has practically completely superseded continental in
area to the left of an axis of a trench (fig. 3). Re = 5,25·10-19;
Gr = 3,2×10-14; Pe = 1255; Ste = 3; g = 9,8.
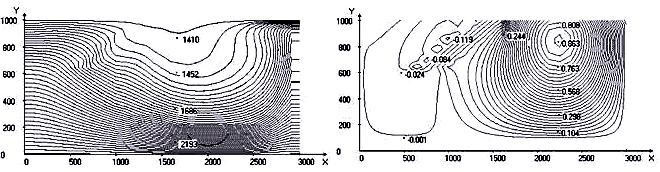
Fig. 3. Calculated fields for j = 300,
Uo = 5: temperature; stream function
On fig.
4 the qualitative
picture of current of a liquid in a subduction zone
for various angle values of a lithosphere feat
is given. Velocity of movement of a continental plate Uk = 1 ñm/year.




j = 600 j = 450 j = 300 j = 150
Fig. 4. Structure of flow current (lines of a stream) Uo = 1; g = 9,8
Analyzing the
results of modeling we can make the following conclusion:
- not taking into account of buoyancy forces conducts
to significant changes in the structure of current;
- the account of gravitational acceleration from mantle depth practically does not influence at thermal and hydrodynamical processes in
subduction zone in comparison with a case when gravitational
acceleration was to constants;
- the received results both
quantitatively, and it is qualitative be
agreed on depth of immersing of a plate in a mantle and under the law of change
of a heat flow on a surface of the Earth with known experimental and
theoretical results of others authors.
Thus, the suggested mathematical model and the
results obtained contribute to the available information on investigation of
convection in the Earth's interior and may be of use for better understanding
and explanation of such phenomena as sea-floor spreading and subduction, lithosphere
plate motion and heat flow change on Earth's surface.