Masich I.S.

Siberian State Aerospace University, Russia

Random and greedy search algorithms

for conditional pseudo-Boolean optimization

The heuristic algorithms for solving conditional pseudo-Boolean optimization problems have been developed and investigated for special problem classes. These algorithms do not demand explicit assignment of functions. The algorithm of adaptive random search of boundary points that combines random search and greedy heuristic has been created.

Most of known at present methods for pseudo-Boolean optimization suppose objective functions and constraints are given by algebraic expressions. At the same time a part of functions or all ones in many real-world problems are given by an algorithm. That circumstance renders impossible to apply usual algorithms of mathematical programming and requires development of search optimization procedures.

Most known heuristic search algorithms are adaptive search algorithms like simulated annealing, genetic and evolutionary algorithms. These algorithms are applied practically for arbitrary optimization problems, but for all that they don’t take account of properties of the current problem classes. Moreover, these algorithms demand tuning of a large number of parameters and don’t have analytic estimations of efficiency.

Recently stochastic and local-stochastic algorithms designing for specific problem classes have became widespread.

In this work heuristic algorithms are created for monotone pseudo-Boolean function optimization problems with monotone constraint function. At that the objective functions and constrains are not required to be defined explicitly.

Consider a problem of the form

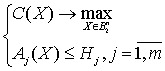, (1)

where and are pseudo-Boolean functions given by an algorithm.

As the optimal solution of the conditional problem is located among boundary points of the feasible solution set, the optimization algorithm must be directed just at search of boundary points.

Consider the problem of monotonically increasing from pseudo-Boolean function optimization with an arbitrary constraint. The optimal solution in that case as shown above belongs to the subset of limiting points of the feasible solution set.

The simplest algorithm for search of the limiting points consists in following [1]. The search starts from . At each step the algorithm chooses a neighboring point in next level moving so in a path of increasing of the objective function up to the bound of the feasible area. If it is necessary, the procedure is repeated for some time, the best point is chosen from the found limiting points.

Random search

1. Put .

2. , .

3. At random choose a point , . If there isn’t such point then to 4 else the cycle is repeated.

4. . If then and to 2.

5. Determine from condition .

Here is the set of all points k-neighboring to X (level k of point X).

Run time of the algorithm equals to

.

Alternative for the random search of the limiting points is a regular algorithm using greedy heuristic.

Consider the problem (1) when the objective function and the constraint are monotonically increasing from pseudo-Boolean functions.

Two greedy strategies are possible for monotone objective function optimization with a monotone constraint: search from the feasible area and search from the area of unfeasible solutions. Accordingly two greedy algorithms have been built: the direct and the dual.

The algorithm of first strategy starts searching from and chooses a feasible point of a next level with the largest specific value on each step. As soon as a found point will be limiting one, it will be taken for the problem solution [2].

Greedy algorithm

1. , .

2. Compute and for , .

3. If there is no for which then is the problem solution.

4. Find 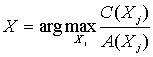from such for which .

5. , to 2.

The regular and stochastic algorithms described in this work transfer the original pseudo-Boolean conditional optimization problem being NP-hard to the problem

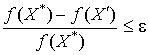
belonging class P (polynomially solvable), where is the optimal solution, is an approximate solution.

The constructed heuristic algorithms allow solving any real-world problem leading to a monotone pseudo-Boolean function optimization problem with imposed restrictions. These algorithms have polynomial estimations of run time and so are oriented mainly for solving the problems of high dimensionality. The follow scheme is the most effective. At first stage the problem is solved with the greedy algorithm, and then some solutions are found by means of the adaptive random search, the best found solution is accepted as the problem solution.

References

1. Antamoshkin A.N., Masich I.S. Heuristic search algorithms for monotone pseudo-boolean function conditional optimization. Engineering & automation problems (Проблемы машиностроения и автоматизации). № 3, 2007, 41-45.

2. Antamoshkin A.N., Masich I.S. Pseudo-Boolean optimization in case of unconnected feasible sets. Models and Algorithms for Global Optimization. Series: Springer Optimization and Its Applications , Vol. 4, edited by A. Törn, J. Žilinskas, Springer, 2007, XVI, p. 111-122.