Математика/4. Прикладная математика

Д.ф.м.-н. Бурова И.Г.

Санкт-Петербургский государственный университет, Россия

О построении численных методов решения задачи Коши на основе неполиномиальных непрерывно-дифференцируемых интегро-дифференциальных сплайнов

В материалах конференции [1] предлагались неявные интерполяционные методы численного решения задачи Коши, полученные с помощью непрерыв-ных интегро-дифференциальных сплайнов. Здесь обсудим построение непре-рывно-дифференцируемых интегро-дифференциальных базисных сплайнов пятого порядка аппроксимации и построение соответствующего численного метода решения задачи Коши.

Пусть - сетка упорядоченных узлов на промежутке [a,b], чебышевская система на . Предполагаем, что определитель Вронского, построенный по системе , отличен от нуля на промежутке . На промежутке функцию , , приближаем с помощью

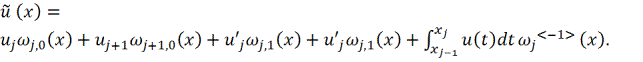
Здесь а базисные функции находим из соотношений

Нетрудно показать, что при

где – однородное дифференциальное уравнение, имеющее фундаменталь-ную систему решений

Пусть

Переходя к переменной получаем формулы

Интегрируя базисные сплайны, получаем

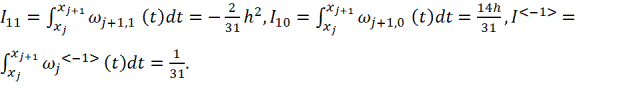
Далее покажем, как построить численный метод для решения задачи Коши

, ∈

Заменяя в формуле Ньютона-Лейбница

подынтегральное выражение на получаем неявный интерполяционный численный метод

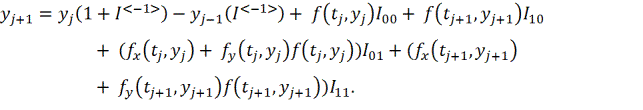
Поэтому, например, в полиномиальном случае имеем правило

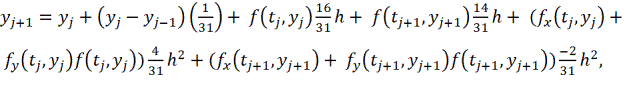
причем для погрешности метода на шаге сетки имеем неравенство

Очевидно легко получить обобщение для решения систем уравнений..

Пример. Будем решать задачу Коши

Очевидно решение этой задачи

Строим приближенное решение с помощью предложенного метода при шаге сетки h=0.01 на промежутке [0, 20]. На рис.1 представлена погрешность решения.

251658240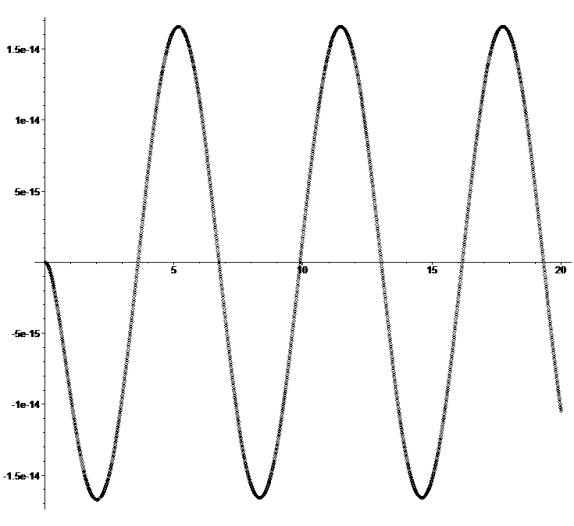Рис.1.График погрешности решения

Литература:

1. Бурова И.Г. Materialy IX mezinarodni vedecko-prakticka konference «Moderni vymozenosti vedy-2013». 27.01.13-05.02.2013. Прага. 2013. С. 3-6.