УДК 539.375.5: 69.058.8

МАТЕМАТИКА. Математическое моделирование

док. техн. наук, проф. Володин Г.Т., асп. Чан Тхань Тунг

Тульский государственный университет, Россия

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАЗРУШЕНИЯ ТОНКИХ ПЛИТ ВЗРЫВОМ

В рамках классических допущений теории изгиба тонких плит,в предположении ближней зоны действия взрыва, с учетом гипотезы упругого режима деформирования пластины вплоть до её разрушения решена задача об определении минимальной массы взрывчатого вещества сферического заряда, взрыв которого приводит к гарантированному разрушению пластины. Задача решена в вариационной постановке с использованием энергетического метода Т. М. Саламахина, согласно которому кинетическая энергия, полученная пластиной от действия взрыва полностью расходуется на работу её упругого деформирования вплоть до разрушения.

Ключевые слова: взрыв, гарантированное разрушение, несущая способность.

1. Физическая модель (основные допущения)

) Рассматривается взрыв сферического заряда конденсированного взрывчастого вещества (ВВ) радиуса с известными физическими характеристиками.

) Заряд ВВ расположен в ближней зоне действия взрыва, вследствие чего давлением окружающей среды можно пренебречь по сравнению с давлением в ударной волне и продуктах взрыва.

) Взрыв происходит в воздухе на некотором фиксированном расстоянии от срединной плоскости пластины.

) Рассматривается пластина прямоугольной формы с размерами постоянной толщины , малой по сравнению с величинами . Принимаются классические допущения теории изгиба пластин.

) Рассматривается случай жесткой заделки пластины по всему контуру.

) Прогибы пластины предполагаются малыми. В процессе деформирования материал пластины ведет себя упруго вплоть до разрушения.

) Кинетическая энергия, полученная пластиной за время действия взрыва, полностью расходуется на работу её упругого деформирования вплоть до разрушения. Разрушение пластины наступает в первом её амплитудном колебании; дальнейшие колебания пластины завершают процессе её разрушения.

Разрушением пластины принято считать потерю её несущей способности вследствие возникновения в ней трещин, сколов, разделений на фрагменты.

2. Математическая модель

Используем прямоугольную декартову систему координат, оси и поместим в срединной плоскости пластины параллельно ее сторонам соответственно и , начало координат – в центре симметрии пластины, ось прогибов направим вертикально вниз (рис. 1)

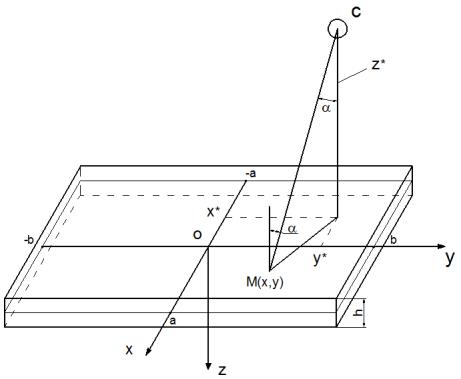
Рис. 1. Схема действия взрывной нагрузки на пластину.

Исследования академика Т.М. Саламахина [3,4] показывают что:

) время действия избыточного давления на преграду не превышает с, поэтому такое кратковременное действие взрывной нагрузки не может быть в полной мере охарактеризовано максимальным значением давления продуктов взрыва; требуется учитывать импульсный характер действующей нагрузки.

) за время действия взрывной нагрузки перемещения деформируемой преграды бесконечно малы, и её деформирование происходит уже после окончания действия нагрузки, в период свободных колебаний.

Введем в рассмотрение интегральную характеристику нагрузки – удельный импульс:

,

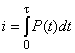где - давление продуктов взрыва, - время, отсчитываемое от момента столкновения первой частицы потока продуктов взрыва с преградой (пластиной) в точке (Рис. 1). Тогда, согласно исследованиям [1,3,4]

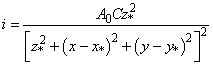, (1)

где -координаты точки, в которой расположен заряд ВВ массы над пластиной. При этом указанные координаты считаются заданными, а масса заряда определяется в результате решения раccматриваемой задачи. Параметр характеризует данное ВВ, например, для тротила м/c [1,4].

Кинетическая энергия, полученная пластиной за время действия на нее взрывной нагрузки, вычисляется в виде [1]

(2)

где - плотность материала пластины,

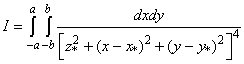(3)

Найдем потенциальную энергию, полученную пластиной в результате её упругого деформирования взрывной нагрузкой.

Упругий потенциал пластины определяется формой её упругой срединной поверхности и, следовательно, является функционалом [5,6]:

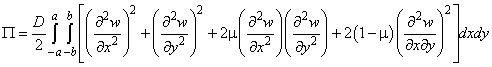(4)

где 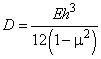-цилиндрическая жесткость пластины, -ее толщина, -модуль упругости материала пластины, -коффициент Пуассона, -прогиб в точке срединной поверхности пластины.

В выражение (4) для упругого потенциала не вошла работа поперечных сил

, , (5)

где , так как соответствующие им сдвиги и , согласно принятой гипотезе прямолинейных элементов равны нулю [5].

Приравняв кинетическую энергию (2) работе деформирования (4), согласно принятому допущению, получим:

(6)

Из соотношений (4), (6) видно, что масса заряда фиксированного ВВ, необходимая для гарантированного разрушения пластины, определяется формой её упругой поверхности , полученной при действии на нее взрывной нагрузки, а также расположением заряда относительно пластины, физическими и геометрическими характеристиками пластины.

3. Решение задачи. Вариационный метод

Используем прямой вариационный метод Ритца. Согласно методу аппроксимации Бубнова-Галеркина, систему координатных функций выберим так, чтобы выполнялись граничные условия закрепления пластины. В рассматриваемом случае жесткой заделки пластины по всему контуру можно предложить систему координатных функций вида:

(7)

Форму упругой поверхности аппроксимируем функцией

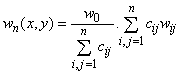(8)

Возьмем и обозначим:

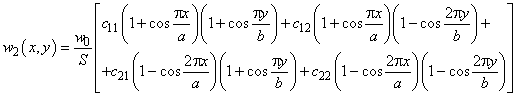(9)

где ; -неизвестные вариационные коэффициенты,

-параметр, определяющий зону разрушения пластины.

Система (7) координатных функций удовлетворяет граничным условиям жесткой заделки пластины по всему контуру опирания:

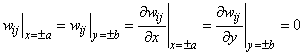(10)

Подставив выражение (9) для предполагаемой функции прогибов в функционал (4), получим функцию в виде:

(11)

где , ,

, ,

, , , ,

Согласно принципу Остроградского-Гамильтона, наиболее близкой к действительной будет та форма упругой поверхности, для которой упругая энергия деформирования имеет минимальное значение, что приводит к системе уравнений:

(13)

Система уравнений (13) может быть преобразована к эквивалентной ей системе уравнений:

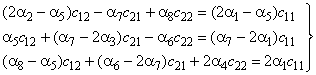
(14)

Вводя обозначения

, , , (15)

получим решение системы (14) в виде:

, , , ,

где

;

;

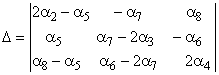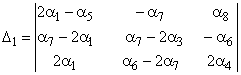
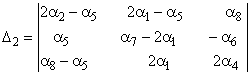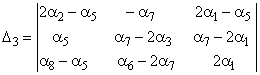
Таким образом, получена форма упругой поверхности, наиболее близкая к действительной в виде:

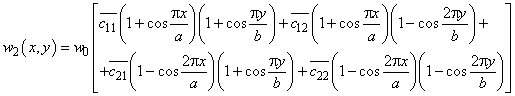(16)

Чтобы найти зону разрушения пластины, а затем и массу заряда ВВ, необходимую для этих целей, воспользуемся критерием разрушения, предложенным П.П. Баландиным [2].

Учитывая при этом динамичность рассматриваемого процесса, а также вероятность возможных отклонений прочностных характеристик материала пластины от нормативных, указанный критерий запишем в виде:

: (17)

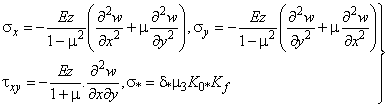где (18)

-предел прочности материала пластины при изгибе в статических испытаниях, -коэффициент динамичности,-коэффициент однородности на гарантированное разрушение, -коэффициент формы[3].

Подставив соотношения (18) и соответствующие им производные в критерий разрушения (17), получим:

, (19)

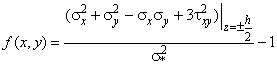где (20)

Неравенство (19) определяет зону разрушения, размеры которой задает параметр .

Если задать размеры зоны разрушения, вводя значение параметра , то используя соотношения (2)-(4),(6), можно определить минимальную величину (массу) заряда ВВ, необходимую для гарантированного разрушения пластины с наперед заданной величиной зоны разрушения:

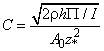(21)

Выполнение соотношения (21) означает, что при фиксированном расположении заряда над пластиной в ближней зоне при величине заряда не меньшей гарантированно при взрыве этого заряда, получим зону разрушения пластины заданной величины, причем вид и расположение зоны разрушения определяется неравенством (19).

Вычисления проведены для различных материалов, размеров пластин, расположений заряда над пластиной в ближней зоне. В качестве примера здесь приведены результаты вычислений для пластины квадратной формы, изготовленной из серого чугуна СЧ 12-28. Расчеты выполнены для значений параметров:

, м, , Па, м, , (взрыв над центром симметрии пластины), , Па, кг/м³, м, м, м/с (ВВ-тротил, плотность кг/м³)

Результаты расчетов представлены на рис. 2

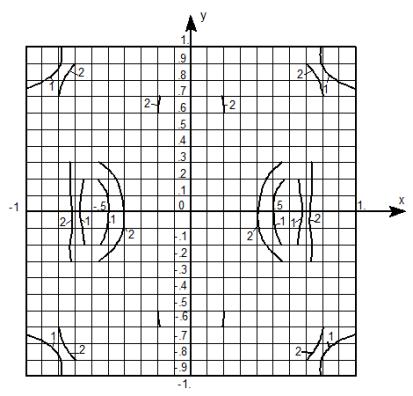
Рис. 2. Область разрушений. Чугун СЧ 12-28,

(1), м,(2)

1)м, кг, м

2)м, кг, м

Кривые с указателем 1, соответствуют значению , а с указателем 2 значению - . При этом кривым 1 соответствует масса заряда кг, а кривым 2 – масса кг.

Расположение кривых 1 и 2 соответствует расположению точек, в которых наступает разрушение пластины с появлением трещин.

Список литературы

1. Володин Г.Т.- Моделирование гарантированного разрушения пластин взрывом неконтактных зарядов конденсированных взрывчатых веществ // Известия ТулГУ. Естественные науки. Вып.1, Ч.1. Тула: Изд-во ТулГУ, 2012. С. 173-183.

2. Баландин П.П.- К вопросу о гипотезах прочности // Вестник инженеров и техников. 1937. №1. С.19-24.

3. Саламахин Т.М.- Разрушение взрывом элементов конструкций. М.: ВИА, 1961, 275 с.

4. Саламахин Т.М.-Физические основы механического действия взрыва и методы определения взрывных нагрузок. М.: ВИА, 1974, 255 с.

5. Филоненно-Бородич М.М.- Теория упругости. М.: ГИФМЛ,1959, 364 с.

6. Володин Г.Т.-Действие взрыва зарядов конденсированных ВВ в газовой и жидкой средах. Часть 2. Врзывостойкость и гарантированное разрушение элементов конструкций // Тула: Левша, 2005, 160 с.