Ковалець О.Я.

Національний технічний університет України «КПІ»

МЕХАНІЧНІ МОДЕЛІ ПРУЖНОЇ ВЗАЄМОДІЇ АКУСТИЧНОГО ВИПРОМІНЮВАННЯ З ТОРЦЯМИ

Найбільш вразливим елементом гіроскопа за натурних умов постає поплавець, всередині якого розміщується гідроагрегат. Сукупна дія пружних переміщень його поверхні під дією проникаючого акустичного випромінювання сприймається гіроскопом як кутова швидкість основи і слугує «хибною» вхідною величиною приладу. Тому найбільша увага в цих дослідженнях приділяється аналізу збуреного стану саме поверхні рухомої частини. Головним спрощуючим припущенням приймається відсутність трансляції енергії згинного руху на сполучені поверхні, що дає підгрунтя для твердження щодо їх шарнірного з‘єднання. Отже, надалі постає можливість здійснення декомпозиції підвісу гіроскопа на окремі плоскі і оболонкові фрагменти і незалежно вивчати дію звукових хвиль на оболонкову частину поплавця та на торцеву. Почнемо з торця.

Розрахункова модель у вигляді нескінченної пластини. В багатьох важливих для практики випадках, в області частот, нижчих від граничної , можна нехтувати впливом граничних умов по контуру пластини і вважати її необмеженою за протяжністю. Стосовно граничних умов на поверхні умовної пластини, тобто на межі води і підводного апарату у вигляді пластини, то умовою їх безвідривної взаємодії є наявність рівності нормальних до поверхні швидкостей човна та оточуючого середовища, а також тиску.

Будуючи модель проходження звукової хвилі крізь умовну пластину, виходимо з наступних припущень: лінійні елементи, які перпендикулярні до серединної поверхні, при деформації залишаються прямими і установлюються вздовж нормалі до викривленої серединної поверхні; в серединній поверхні не виникають деформації подовження або зсуву; деформації при згині залишаються малими, пружними і підпорядкованими закону Гука.

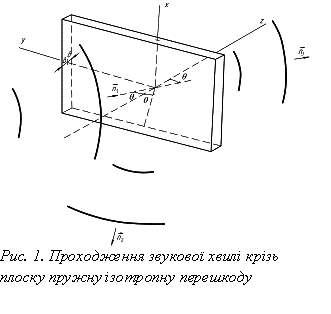Вивчення явища зробимо на прикладі плоскої монохроматичної хвилі тиску, тобто такої хвилі, в якій відсутні градієнти тиску і швидкості переміщення середовища вздовж лінії фронту. Окрім того, швидкість часток середовища у плоскій хвилі пропорційна тиску в той же момент часу. На практиці плоску хвилю розглядають як ідеалізацію хвилі, що випромінюється тілом обмежених розмірів і, при цьому, знаходиться на значній відстані від об’єкту. Вирішення поставленої задачі проілюструємо на широко використовуємій в акустиці механічній моделі (рис. 1). Отже, ізотропна пружна пластина сталої жорсткості і необмеженої протяжності розділяє два акустичні напівпростори. Приймемо, що на лицьову поверхню пластини під кутом падає плоска монохроматична хвиля звукового тиску

(1)

де – хвильове число; – кутова частота коливань; – швидкість звуку; – амплітуда тиску у звуковій хвилі.

Величина при координаті введена для зручності подальших обчислень. Відбита та пройдешня хвилі, відповідно, мають вигляд:

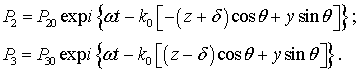(2)

Виходячи з наведеного, згинний рух пластин реалізується в площині і не залежить від координати , що пояснюється відсутністю градієнта тиску вздовж цієї координати.

За прийнятих спрощень, має місце плоска деформація. У формі Ламе її аналітичний опис має вигляд:

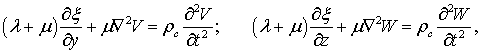(3)

де 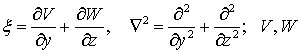– пружні переміщення поверхні в напрямку осей ; – щільність матеріала пластини; – сталі Ламе.

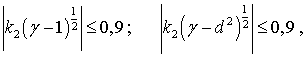(4)

що обумовлює присутність лише перших двох членів розкладання в ряд величин у співвідношеннях (3), (4), згин пластини під дією симетричної та антисиметричної складових, відповідно, набуває виду –

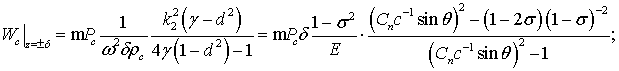(5)

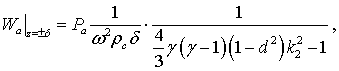(6)

де 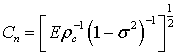– швидкість поздовжніх хвиль в пластині.

Якщо , тоді перший доданок в знаменнику стає суттєво малим, у порівнянні з одиницею, і формула (6) спрощується:

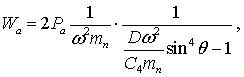(7)

де 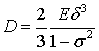циліндрична жорсткість пластини на згин; – питома маса.

Формула (7) відображує відомий закон згинних коливань тонкої пластини.