Ковалець О.Я.

Національний технічний університет України «КПІ»

ВЗАЄМОДІЯ АКУСТИЧНОЇ ХВИЛІ З КОЛОВОЮ ПЛАСТИНОЮ

Дослідження ряду учених довели, що в багатьох важливих для практики випадків в області частот нижче граничних , умови закріплення пластин не впливають на її динаміку і, таким чином, не порушуючи об‘єктивності картини проходження звуку, можна нехтувати дією граничних умов по контуру кріплення, отже вважати її нескінченною за протяжністю.

Граничними умовами вважається розподіл параметрів на граничній поверхні, а також на нескінченності (для необмеженої області) і на початку координат (для області визначених параметрів).

Стосовно граничних умов на поверхні пластин, то на межі середовища з підатливим (деформуємим) тілом, тобто пластиною, умова безвідривної взаємодії полягає у рівності нормальних до поверхні швидкостей руху тіла (поплавця) і середовища (важкої органічної рідини, в якій знаходиться у зваженому стані поплавець), а також тиску.

Будуючи математичну модель проходження звуку крізь торцеву пластину визначимо наступні припущення: лінійні елементи пластини, які перпендикулярні до її серединної поверхні, за деформації залишаються прямими і встановлюються до викривленої серединної поверхні; в серединній поверхні не виникають деформації здовження або зсуву; деформації пластини при згині залишаються малими, пружними і підпорядковані закону Гука.

Явище будемо вивчати на прикладі плоскої монохроматичної хвилі тиску, тобто хвилі з плоским фронтом, тиск і швидкість переміщення часток середовища в котрій не мають градієнта вздовж лінії фронту. Окрім того, швидкість часток середовища у плоскій хвилі вважаємо пропорційною тиску у той же момент часу. На практиці плоску хвилю розглядають як ідеалізацію хвилі, що випромінюється тілом обмежених розмірів, яке знаходиться на значній відстані.

Аналіз природи проходження звуку крізь пластини, які не з‘єднані між собою, проводився А. Лондоном [21], а більш узагальнена теорія дії звуку на складені конструкції викладена, наприклад, в роботах.

Вплив пружності на коливання конструкції в рідині вперше вивчався Релеєм (Джон Уильям Стретт, Lord Rayleigh) [25], а потім Николаї при розгляді коливань нескінчених за протяжністю циліндричних оболонок і Лембом [27]. Ці роботи грунтувались на припущенні співпадання форм коливань пружних тіл у рідині та в порожнечі.

Особливістю робіт останнього часу було ускладнення моделей рідини і пружного тіла, а також урахування більшого числа збурюючих чинників.

Суттєвими відмінами можна назвати наступні:

- відмова від гіпотези подібності форм коливань у порожнечі та в рідині;

- застосування до розв‘язку задач метода розкладення за власними функціями деякої крайової задачі, а не за формами коливань;

- розробка асимптотичних методів розрахунку коливань;

- складання таблиць частот власних коливань у широкому діапазоні зміни параметрів збурюючих чинників, а також фізичних властивостей об‘єктів.

Механічну модель проходження акустичного випромінювання крізь торцеву пластину поплавця наведено на рис.1.

З лівої, лицьової, сторони торця падає плоска монохроматична хвиля тиску в напрямку , нормалі до фронту. Падаючу, дифракційну та пройдешню хвилі позначимо відповідно цифрами 1, 2 та 3. Товщину пластини приймемо рівній , а радіус - . Систему координат зв‘яжемо із серединною площиною, а точку розташуємо у геометричному центрі пластини. Цілком зрозуміло, що торець найбільше вразливий дії випромінювання у напрямку нормалі до поверхні, бо саме тут імпеданс мінімальний порівняно із двома іншими вимірами.

Диференціальне рівняння збудженого руху у формі Софі Жермен має вигляд:

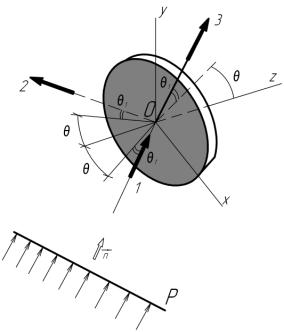
Рис.1. Схема проходження звукової хвилі крізь колову пластину

(1)

де 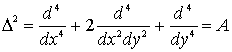- бігармонічний оператор;

- циліндрична жорсткість, щільність матеріалу, товщина і коефіцієнт Пуасона відповідно.

Торець коливається відносно площини . Рівняння (1) слушне в площині , котра знаходиться в системі . Розв‘язання шукаємо для . Це рівняння дає задовільні результати у разі відношення товщини пластини торця до найменшої довжини генеруємої хвилі не більше 0,1. В інших випадках слід враховувати зсув та інерцію обертання, або розв‘язувати тривимірну задачу.