Бойков И.В., Кривулин Н.П., Мойко И.М., Мойко Н.В.

Применение преобразования Хартли для определения импульсной переходной функции динамических систем.

В работе предлагается метод востановления импульсных переходных функций динамических систем, описываемых интегральными уравнениями Вольтерра второго рода

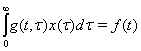(1)

Метод основан на применении интегрального преобразования Хартли [] для уравнения (1). Рассмотрим преобразование Хартли [2] к системе, состоящей из двух уравнений, и полученной в результате подачи на вход динамической системы двух тестовых сигналов.

В работе используется интегральное преобразование

. (2)

Тогда обратное преобразование определяется формулой

. (3)

Где

Утверждение: пусть функция удовлетворяет условию

, (4)

где - некоторая заданная функция.

Тогда применяя интегральное преобразование (2) к уравнению (1) получим

(5)

где - преобразование (2) функций .

Действительно, применяя интегральное преобразование (2) к уравнению (3) и используя условие (4), имеем:

.

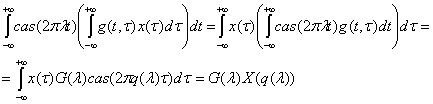Из этого выражения следует формулы справедливость (5). Отметим, что данное утверждений является обобщением теоремы Бореля [4], полученное для интегрального преобразования Лапласа. Аналогичные результаты получены для преобразования Фурье в работе [3].

Рассмотрим динамическую систему, описываемую уравнением (1), у которой входной сигнал, выходной сигнал и импульсная переходная функции, удовлетворяющая условию (4).

Требуется восстановить функцию .

Пусть и два линейно-независимых входных сигнала. Тогда

(6)

Применяя интегральное преобразование (2) к системе интегральных уравнений (6) получим систему нелинейных алгебраических уравнений

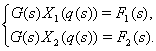(7)

с неизвестными функциями и Решая систему (7) относительно этих функций, находим и Функция может быть найдена применением преобразования обратного преобразованию (3) или из решения интегрального уравнения

.

Для вычисления последнего интеграла можно использовать различные вычислительные методы. Наиболее удобным является использование квадратурных формул [1].

Рассмотрим применение нескольких интегральных преобразований для определения импульсной переходной функции.

Требуется восстановить функцию системы описываемой интегральным уравнением (1).

Рассмотрим интегральные преобразования

(8)

Пусть функция удовлетворяет условиям

, (9)

Где - определяет ядро некоторого интегрального преобразования, например Лапласа, Фурье, Меллина, Хартли.

Пусть и два линейно-независимых входных сигнала. Тогда

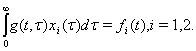(10)

Применяя интегральные преобразования (8) к системе интегральных уравнений (10), учитывая (9) получим систему нелинейных алгебраических уравнений

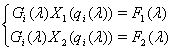(11)

с неизвестными функциями и Решая систему (11) относительно этих функций, находим и

Тогда функцию будем находить в виде

Где коэффициенты находятся методом наименьших квадратов из условия

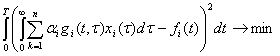
Функции находятся как обратное преобразование (3) или из решения интегральных уравнений

Литература

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Наука, 2009. 630 с.

2. Брейсуэл Р. Преобразование Хартли : Пер. с англ. – М.: Мир, 1990. – 175с.

3. Бойков И. В., Кривулин Н. П. Определение временных характеристик линейных систем с распределенными параметрами // Метрология. 2012. № 8. С. 3–14.

4. Эфрос А.М., Данилевский А.М. Операционное исчисление и контурные интегралы. Харьков: Государственное научно-техническое издательство Украины. 1937. 384 с.