Математика / 4. Прикладная математика

К.б.н.Артеменко М.В., Смирнов В.С.

Юго-западный государственный университет

ИСПОЛЬЗОВАНИЕ ДОПОЛНИТЕЛЬНОГО ДИАГНОСТИЧЕСКОГО МНОЖЕСТВА ФОРМИРОВАНИЯ РЕШАЮЩИХ ПРАВИЛ В УСЛОВИЯХ НЕЧЕТКОСТИ

Эксплуатация автоматизированных систем поддержки принятия решений в условиях неопределенности и нечеткости «входной» информации более оптимальна при использовании методологии мягких вычислений, позволяющей позволяет проектировать экспертные системы [1]. В основе функционирования указанных систем лежат предварительно идентифицированные вывода, направленные на решение задач: классификации (диагностики), интерполяции и экстраполяции.

Нечеткий вывод реализуется на определенном наборе правил, по которым вычисляется значение истинности для предпосылки применения каждого правила на основании нечетких операций - термов в левой части правил [2] - это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации.

Различными авторами и научными школами предлагаются разнообразные способы построения нечеткой импликации. Наибольшее распространение получили следующие способы нечеткого логического вывода [2]:

- Алгоритм Мамдани (Mamdani). Импликация определяется минимумом, а агрегация – максимумом;

- Алгоритм Цукамото (Tsukamoto). Исходные посылки – как у предыдущего алгоритма с учетом предположения о монотонности поведения функции принадлежности;

- Алгоритм Суджено (Sugeno). Алгоритм обусловливается тем, что правые части правил вывода представляются линейно;

- Алгоритм Ларсена (Larsen). В этом случае Ларсена нечеткая импликация осуществляется операцией умножения;

- Упрощенный алгоритм нечеткого вывода. Исходные правила задаются в виде: Если X есть А_i и Y есть B_i , то z=Z_i, где Z_i – четкое значение.

После применения любого из указанных правил рекомендуется выходную функцию принадлежности масштабировать с учетом вычисленной степени истинности предпосылки правила [2].

Анализ приведенных правил вывода, показывает, что в них не учитывается значения переменных (носителей), как аргументов. Кроме того, их обилие требует введение дополнительного критерия для альтернативного выбора определенного правила (на основе либо субъективного анализа [3] либо объективного – например, степени риска принятия решения в дальнейшем).

Таким образом, возникают противоречия интерпретации результатов и связанные с этим проблемы функционирования систем поддержки принятия решении в условиях неопределенности и нечеткости анализируемой информации.

В качестве одного из способов разрешения указанной проблемы предлагается следующий подход к формированию и использованию правил вывода. Основная идея заключается в том, что значение функции принадлежности результата диагностического решения, полученного на основе решающих правил определенных на первоначальном и дополнительных множествах, определяется значениями функций принадлежности указанных множеств (или лингвистических переменных) и ранее определенными ЛПР (лицом принимающим решение) пороговыми значениями соответствующих функций принадлежностей, ниже уровня которых вероятность принадлежности значения анализируемого элемента множеству малозначима (принятие решения по признакам неприемлемо для адекватного диагностического решения).

Пусть имеются два нечетких диагностических множества , и определены два пороговых значения функций принадлежности - соответственно, . (Заметим, что оба множества являются диагностическими, т.е. элементы в них входящие характерны, хотя и могут быть и не определяющими, для определенного класса анализируемого объекта – например, заболевания). Значение по сути является уверенностью правильности принятого диагностического решения на определенном элементе множества , причем указанная уверенность не удовлетворяет ЛПР (лицо принимающее решение) или соответствующие алгоритмы системы поддержки принятия решений по определенным внешним критериям. В этом случае, предполагается использование дополнительного диагностического (в общем случае нечеткого) множества , что позволит достичь приемлемого решения.

В теории классификации, основанной на нечетких множествах рассматриваются различные способы оценки значений функции принадлежности диагностических правил, полученных при использовании информации дополнительного множества в зависимости от того, какой закон логического соединения множеств и определяется ЛПР [2], исходя из целей исследования и/или дальнейшего управления (в том числе, терапевтическим процессом).

Учитывая введенные пороговые значения предлагается вычислять значения функции принадлежности с учетом дополнительной информации множества , представленной в Таблице 1. В зависимости от полученных значений и , применяются различные формулы (представлены в ячейках Таблицы 1) для вычисления значения функции принадлежности итогового решающего диагностического правила. Согласно предлагаемым формулам реализуется парадигма усиления качественных свойств обобщенного результата: уменьшение значений в наихудшем сочетании и увеличении в наилучшем.

Пороговое значение для и значения коэффициентов предлагается определять либо экспертным путем, либо используя опыт ЛПР, либо идентифицировав функциональную зависимость от характеристик множеств , и на обучающей выборке с учетом удовлетворяющего ЛПР результата решения диагностической задачи.

Таблица 1. Формулы определения функции принадлежности совместного использования , :

			,

Результаты вычислительного эксперимента (средствами Mathcad 7.0) поведения функции (где - функция принадлежности, определяющая нечеткость применения решающего диагностического правила при совместном применение множеств и ) при , приведены на Рисунке 1 (3D) и Рисунке 2 («топология» - для лучшего восприятия значения функции масштабированы с коэффициентом 100). Хорошо заметна некоторая неустойчивость на границе пороговых значений.

Таким образом, предлагаемый подход применения различных формул для вычисления значений результирующей функции принадлежности позволяет оптимизировать процесс анализа на объективной основе, что в целом способствует более качественному проектированию и эксплуатации систем поддержки принятия решений в условиях неопределенности и необходимости привлечения дополнительной информации в виде соответствующего множества.

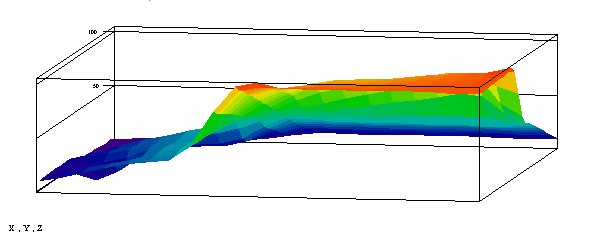Рисунок 1. Поведение результирующей функции (соответственно оси: Х-, Y - , Z - ).

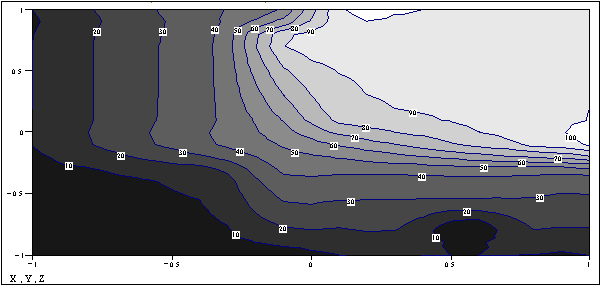
Рисунок 2. Контурная топология поведения результирующей функции (соответственно оси: Х-, Y - , Z - ).

Литература:

1. Прикладные интеллектуальные системы, основанные на мягких вычислениях / под. ред. Н.Е. Ярушкиной. –Ульяновск, УлГТУ, 2004. 139 с.

2. Яхъева Г.Э. Нечеткие множества и нейронные сети: учебное пособие. –М.: Интернет-Университет Информационных Технологий; Бином. Лаборатория знаний, 2010. – 316 с.

3. Касьянов В.О. Суб'єктивний аналіз: Монографія. – К.:НАУ, 2007. 512 с. – Рос. Мовою.