Д.т.н. Володин Г.Т., Новиков А.С.

Тульский государственный университет, Россия

Гарантированное разрушение оболочечных конструкций взрывной нагрузкой

 

Нахождение условий разрушения оболочечных конструкций является актуальной проблемой при проектировании несущих элементов конструкций взрывоопасных производств, определении технических условий при проектировании складов боеприпасов, утилизации крупногабаритных элементов конструкций, при проектировании взрывозащитных инженерных сооружений и др. Важно определить форму и величину заряда ВВ, при взрыве которого на некотором расстоянии от оболочечной конструкции, гарантированно произойдет её разрушение. Под разрушением понимаем потерю несущей способности оболочки вследствие появления в ней трещин, сколов, разделений на фрагменты.

Физическая модель (основные допущения)

Рассмотрим тонкую открытую цилиндрическую оболочку, выполненную из упругого материала, постоянной толщины h с радиусом кривизны R, защемленную в идеальных (недеформируемых) опорах, с размером плана 2а×2b м (рис. 1). Оболочку принято считать тонкой, если  [1]. Материал оболочки предполагается однородным и изотропным. Рассматривается упругий режим деформирования вплоть до ее разрушения. Принимаются основные классические гипотезы теории тонких оболочек (гипотеза прямолинейного элемента и гипотеза пренебрежимой малости нормальных напряжений, в слоях параллельных срединной поверхности). На расстоянии hZ от поверхности оболочки, над центром симметрии плана оболочки, располагается сосредоточенный сферический заряд взрывчатого вещества радиуса r0 и массой С, тип и энергетические характеристики которого определяются обобщенным параметром А0 (например, для тротила А0=400 м/с) [2]. Рассматривается ближняя область действия взрыва  [2], для которой давлением окружающей среды можно пренебречь по сравнению с давлением продуктов взрыва. Прогибы оболочки могут быть одного порядка с толщиной [8].

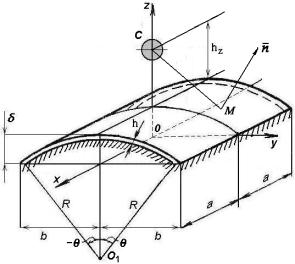
Рис. 1. Схема расположения заряда ВВ над оболочкой при взрыве

Математическая модель и решение задачи

Введем прямоугольную декартову систему координат Oxyz с началом в центре симметрии плана оболочки (рис. 1). Обозначим δ – стрелу подъема оболочки над планом, О1 – центр кривизны, 2θ – угол, определяющий длину дуги цилиндрической оболочки радиуса R. Вследствие гипотезы о малой толщине оболочки рассматриваются перемещения точек ее срединной поверхности [6].

 Пусть в начальный момент времени  происходит взрыв указанного ранее сферического заряда. Как показали исследования Т.М. Саламахина [2], возникшая взрывная нагрузка носит импульсный характер, вследствие ее кратковременности действия (время действия не превышает 2×10-4с). Поэтому за время ее действия точки оболочки не получают заметных смещений, а получают только начальные скорости. Таким образом, импульсный характер динамической нагрузки эквивалентен сообщению точкам элемента конструкции начальных максимальных скоростей. Также Т.М. Саламахин показал [2], что при относительных расстояниях , удельный (по площади) импульс взрывной нагрузки i, действующий на плоский элемент преграды, может быть вычислен по формуле

                                                (1)

где r – расстояние от точки М до центра заряда ВВ, φ – угол падения (угол образованный скоростью потока продуктов взрыва с нормалью к поверхности преграды). Применим энергетический метод, предложенный Т.М. Саламахиным [5], согласно которому кинетическая энергия, полученная оболочкой за время действия взрыва, полностью расходуется на работу ее деформирования вплоть до разрушения

                                                       (2)

Кинетическая энергия, полученная элементом оболочки массой dm в точке M(x,y,z), согласно импульсному характеру действующей на него взрывной нагрузки, вычисляется в виде

                                                (3)

где dm=ρhdS, ρ – плотность материала оболочки, dS – площадь элементарного участка, окружающего точку M. Скорость V, получаемая рассматриваемым элементом в начальный момент времени, определяется из теоремы об изменении количества движения материальной точки

                                                   (4)

где I=idS – импульс, действующий на элемент оболочки площадью dS. После подстановки (4) в (3) получим, с учетом выражения (1)

                                         (5)

где .

Следовательно кинетическая энергия Э, полученная всей цилиндрической оболочкой за время действия взрыва, с учетом (5), выразится в виде

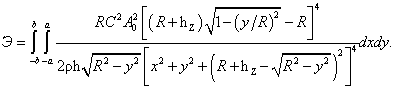                 (6)

Найдем теперь работу деформирования П цилиндрической оболочки взрывной нагрузкой. Известно [6], что компоненты тензора деформаций для введенной системы координат Oxyz (рис. 1.) имеют вид

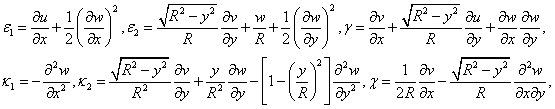     (7)

где u=u(x,y), v=v(x,y), w=w(x,y) – компоненты вектора перемещения для точки М. Исходя из (7), согласно [6], получим соответствующие выражение для П

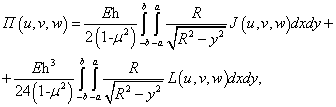                (8)         

где

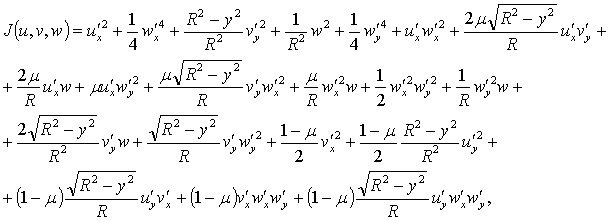
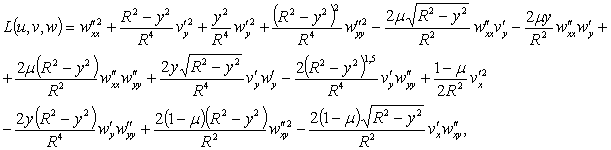
где штрихи у функций u=u(x,y), v=v(x,y), w=w(x,y) с индексами обозначают соответствующие им дифференциальные операторы частного дифференцирования. Из выражения (8) видно, что работа П упругого деформирования оболочки зависит от вида функций u=u(x,y), v=v(x,y), w=w(x,y) и, следовательно, является функционалом. Согласно принципу Остроградского-Гамильтона наиболее близкой к действительной форме упругой поверхности будет та форма, определяемая функциями u=u(x,y), v=v(x,y), w=w(x,y), для которых упругий потенциал П имеет минимальное значение, что приводит к вариационной задаче нахождения минимума функционала (8).

Используем прямой вариационный метод Ритца, согласно которому приближенное решение вариационной задачи представляют в виде линейной комбинации системы координатных функций с варьируемыми коэффициентами, и удовлетворяющими граничным условиям задачи

                                     (9)

где un(x,y), vm(x,y) и wp(x,y) соответствуют виду закрепления оболочки, в рассматриваемом случае – отсутствию прогибов по всему контуру закрепления и углов поперечных поворотов сечений оболочки на контуре

 при x=±a,

 при y=±b,

 при x=±a,

 при y=±b.

Для приближения n=1, m=1, p=1

    

                 (10)

Заметим, что константа w0 в выражении (9) предполагается неварьируемой, через нее определяется величина области разрушения материала оболочки, а для определения cku, ckv, ck используем принцип минимума потенциальной энергии, откуда следуют необходимые условия минимума

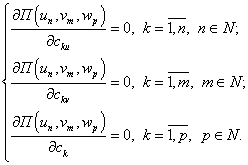                              (11)

Из системы уравнений (11) выразим cku=cku(w0), ckv=ckv(w0), ck=ck(w0). Тогда выражение (10) примет вид

              (12)

Если задать параметр w0, то воспользовавшись одним из критериев разрушения, можно определить область разрушения материала оболочки и ее величину (протяженность), а так же соответствующую ей величину массы С заряда ВВ, взрыв которого гарантирует такую область разрушения. Воспользуемся критерием энергии формоизменения [7]. Согласно введенным ранее основным гипотезам теории тонких оболочек этот критерий приводит к соотношению

                                     (13)

где

          (14)

а К – коэффициент, показывающий во сколько раз увеличивается статический предел текучести при растяжении σТ  материала оболочки при его динамическом нагружении. При этом, для выражения (14) имеем [6]

                        (15)

где Н – расстояние между срединным и некоторым фиксированным слоем оболочки,

После подстановки в критерий разрушения (13) выражений (14), (15), (7), с учетом (10), для приближения n=1, m=1, p=1 получим соотношение

                                      (16)

где функция Ω вследствие ее громоздкости здесь не приводится.

Равенство в соотношении (16) определяет «минимальную» линию уровня, на которой выполняется критерий разрушения (13), соответствующий минимальной массе С заряда ВВ. Вычисления проводились для оболочек разных размеров и разных материалов с различными случаями расположения зарядов над оболочкой. Здесь в качестве примера приведены результаты вычислений для открытой цилиндрической оболочки, выполненной из стали марки 08Х13, со следующими геометрическими и механическими параметрами: a=0.5м, b=0.35м, R=0.5м, м, h=5·10-3м, Н=±0.5h, μ=0.31, ρ=7.7·103 кг/м3, Е=22·1010 Па, К=1.6, σT =2.8·108 Па, параметр А0 для заряда ВВ (литой тротил) равен 400 м/с. Положим w0=7, тогда для выражения (12)

, , ,

при этом зоны разрушения, для слоев H=0.5h и H=-0.5h, определяемые соответствующими линиями уровня, для рассматриваемых слоев приведены на рисунке 2.

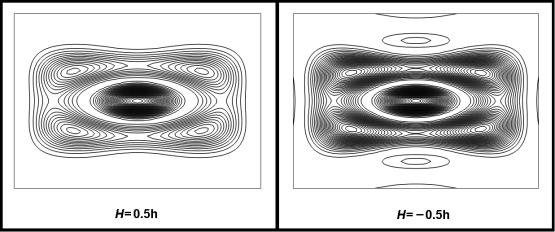
Рис. 2. Зоны разрушения

Согласно соотношениям (2), (6), (8) найдем зависимость массы заряда С от расстояния hZ. Например, для значения ближней зоны hZ=0.2м С=0.1кг, hZ=0.3м С=0.16 кг, а для hZ=0.4м С=0.228 кг.

 

Библиографический список

1. Новожилов В.В. Теория тонких оболочек. Л.: ГСИСП, 1962. 432 с.

2. Саламахин Т.М. Физические основы механического действия взрыва и методы определения взрывных нагрузок. М.: ВИА, 1974. 255 с.

3. Володин Г.Т. Действие взрыва зарядов конденсированных ВВ в газовой и жидкой средах. Часть 2. Взрывостойкость и гарантированное разрушение элементов конструкций. Тула: Левша, 2005. 160 с.

4. Володин Г.Т. Прямой вариационный метод исследования взрывостойкости и гарантированного разрушения балочных конструкций взрывной нагрузкой // Вестник Тульского государственного университета. Серия Дифференциальные уравнения и прикладные задачи. Вып. 1. 2009. С. 49–54.

5. Саламахин Т.М. Разрушение взрывом элементов конструкций. М.: ВИА, 1961. 275 с.

6. Колкунов Н.В. Основы расчета упругих оболочек. М.: Высшая школа, 1963. 278 с.

7. Гольденблат И.И., Копнов В.А. Критерии прочности и пластичности конструкционных материалов. М.: Машиностроение, 1968. 191 с.

8. Вольмир А.С. Нелинейная динамика пластинок и оболочек. М.: ГРФМЛ, 1972. 433 с.