Математика/5. Математическое моделирование

Д.ф.-м.н., Байманкулов А.Т., Махамбетова Г.И.

Костанайский государственный университет им.А.Байтурсынова, Казахстан

АПРИОРНЫЕ ОЦЕНКИ РАЗНОСТНОЙ ЗАДАЧИ

Рассмотрим разностный аналог задачи (1) - (4), рассмотренной в [3, с.45-46],

(1)

, . (2)

Умножив (1) на и просуммировав по всем внутренним узлам

сетки

получим выражение

. (3)

После суммирования по частям и использования граничных условий (2) имеем неравенство:

-

. (4)

Применив к (4) неравенство Коши и проведя элементарные преобразования, получим неравенство

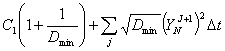, (5)

где

.

Из очевидного тождества

следует неравенство:

.

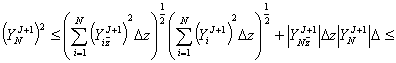
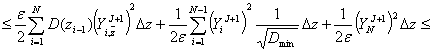Преобразуя, получим

.

выбирается так, чтобы 1-. Тогда при имеем

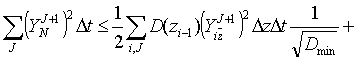
. (6)

Неравенство (5) усиливается на основе (6)

.

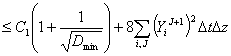Применяя разностный аналог леммы Гронуолла, выводим, что:

.

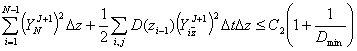С учетом (6), выводим оценку

.

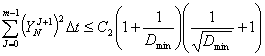Лемма 5. Если , , , то для решения задачи (1)- (2) имеют место оценки:

,

.

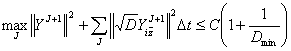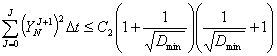Литература

1.Нерпин С.В., Юзефович Г.И. О расчете нестационарного движения влаги в почве// Доклады ВАСХНИЛ, № 6, 1966.

2.Юзефович Г.И., Янгарбер В.А. Исследование нелинейного уравнения влагопереноса. // Л.: Колос. Сб. трудов по агрофизике, вып. № 14, 1967.

3.Байманкулов А.Т. Определение коэффициента капиллярной диффузии.// Материали за VIII международна научна практична конференция «Бъдещето въпроси от света на науката -2012», т.36, 17-25 декември, 2012, София.