Проф., д.т.н. Гданский Н. И., доц., к. т. н. Карпов А. В.,
доц., к.пед.н. Рысин М. Л.

Российский государственный социальный университет, Россия

Применение информационно-тестирующих систем для адаптивного управления учебным процессом

В статье рассмотрены вопросы разработки и практической реализации в учебном процессе при преподавании дисциплин технического цикла информационно-контролирующих систем, построенных на базе стандартных систем управления учебным процессом.

Использование стандартных LMS (Learning Management System) создает возможности для: активизации учебного процесса за счет создания информационной образовательной среды современного уровня, создания условий для активного взаимодействия студентов с информационной образовательной средой в дополнение к традиционным формам обучения, повышение личной компетентности студентов и обучение их навыкам самостоятельной работы путем ее рациональной организации на современном уровне развития информационных технологий.

Однако при дополнительном расширении функций стандартных LMS с их помощью можно решать задачи более высокого уровня. В частности, на основе более глубокого контроля реальных знаний обучающихся производить адаптивную коррекцию учебного процесса в течение семестра.

Для решения поставленной задачи, прежде всего, необходимо правильно структурировать методические материалы по преподаваемой дисциплине. По функциональному назначению все материалы разбиты на два основных блока – информационный и тестирующий.

Оптимальный состав основных материалов для односеместровой дисциплины следующий.

Информационный блок состоит из 3–5 разделов с размерами от 20 до 40 страниц информативного текста. Каждый раздел состоит из 3–5 подразделов с размерами от 5 до 12 страниц. Каждый информационный подраздел содержит все необходимые теоретические сведения, а также примеры решения всех необходимых видов практических заданий.

Тестирующий блок. Минимальной тестируемой единицей изучаемой дисциплины является подраздел, поэтому тестирующие материалы привязываются к соответствующим подразделам разделов изучаемой дисциплины. Также предусматривается входное тестирование для проверки остаточных знаний по ранее изученным предметам.

Тестирование по назначению подразделяется на:

· учебное, проводимое самостоятельно для оценки знаний самим обучающимся,

· контрольное, проводимое под наблюдением преподавателя (тьютора) для объективной оценки реального уровня знаний.

Практически данные возможности обеспечиваются применением двух различных алгоритмов тестирования.

Учебное тестирование всегда выполняется по подразделам. Результаты анализа ответов на каждый теоретический вопрос и решение каждой задачи оперативно объявляются обучающемуся. Также в результате анализа текущих ответов адаптивно формируется траектория контроля – выбирается число и содержание очередных вопросов и практических заданий.

В конце опроса выставляется общая оценка в баллах и, если необходимо, общие рекомендации по повторному изучению материала.

Контрольное тестирование может выполняться по подразделам, разделам и всему курсу – в зависимости от запроса. Для сокращения времени опроса текущие результаты контроля не объявляются обучающемуся. В конце опроса выставляется общая оценка в баллах. Независимо от уровня контроля для системного группового анализа знаний формируется парциальная балльная оценка знаний в отдельности по каждому подразделу.

Каждый тестирующий блок подраздела содержит базовый набор из 20-30 вопросов для проверки теоретических знаний. Если тестируется обзорный материал, не содержащий глубоких теоретических выкладок либо методов решения задач, то данный материал является достаточным для проверки знаний.

Если же подраздел содержит теоретические материалы и/или методику решения задач, то базовый тестирующий раздел в зависимости от содержания учебного материала целесообразно дополнить следующими материалами: теоретическими вопросами повышенной сложности; задачами; задачами повышенной сложности. В сумме число k предлагаемых видов тестирующих материалов по подразделу не должно превышать 3. В зависимости от числа k предлагаемых уровней тестирования (1, 2 или 3) соответствующую схему тестирования назовем 1-, 2- и 3-уровневой.

Практически данные возможности обеспечиваются организацией информационного и тестирующего материала по подразделам курса и учитываются в тестирующих алгоритмах.

Стратегии опроса и оценивания должны учитывать размер тестируемого материала дисциплины (подраздел, раздел, весь курс), а также имеющиеся тестовые материалы (1-, 2- или 3-уровневый).

1-уровневое тестирование. Предложено производить при помощи 1-2 фаз опроса в зависимости от правильности ответов на первой базовой фазе. Если после базовой фазы опроса нет отрицательного ответа, то используется вторая фаза опроса с сокращенным числом вопросов (вдвое меньшей по сравнению с базовой), которую назовем уточняющей.

Для иллюстрации стратегии опроса и оценивания знаний по одноступенчатым тестировочным материалам предложено использовать t-деревья, где t – число тестовых заданий первой базовой фазы опроса. Рассмотрим построение 4-дерева.

Принцип оценивания следующий: при наборе на первой фазе опроса 0 знания учащегося оцениваются в минимальную сумму 0 баллов, и он исключается из дальнейшего тестирования. При получении 4 баллов из 4 знания учащегося оцениваются в максимальную сумму 100 баллов, и он также исключается из дальнейшего тестирования. Таким образом, при равномерном распределении оценок получается, что каждый правильный ответ оценивается в 100/4=25 баллов.

При получении от 1 до 3 баллов в первой фазе производится уточняющий опрос с заданием 4/2 = 2 тестов из того же набора. Для оценки баллов за каждый правильный ответ предложено исходить из того, что при 3 правильных ответах в первой фазе и максимальных 2 правильных ответах во второй фазе должна получиться сумма, несколько меньшая 100 баллов. Принимая такую сумму равной 95 баллов, получим, что каждый правильный ответ на уточняющий тест должен оцениваться в (95 – 75)/2 = 10 баллов. Алгоритм одноступенчатого тестирования проиллюстрирован на дереве опроса на рис. 1.

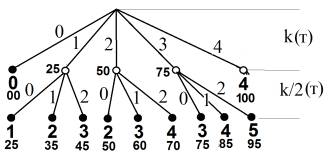
Рис. 1. Схема алгоритма одноступенчатого тестирования

2-уровневое тестирование. Вначале необходимо установить распределение максимальных баллов, получаемых в первой и второй фазе опроса. Принято, что при максимальном результате на первой фазе обучающийся может получить несколько больше половины максимального числа баллов. Возьмем это число равным 60. Тогда стоимость одного правильного ответа в первой фазе будет равна 60/4 = 15 баллов. Поскольку 100 баллов соответствуют 2 правильным ответам на вопросы повышенной сложности, то стоимость каждого такого правильного ответа равна
(100 – 60)/2 = 20 баллов. Если на втором этапе используются обычные тестовые вопросы, то их стоимость принимается меньше, чем 20 баллов, т.е. равной 15.

Обозначим число правильных ответов в первой фазе через t₁. Число неверных ответов – через f₁. При этом t₁ + f₁ = k. В зависимости от результатов первой фазы (t₁) предложено выбрать два дальнейших продолжения.

1. Обучающийся набрал не более половины максимального числа баллов: t₁ £ k/2.

При t₁ = 0 считается, что у обучающегося полное отсутствие знаний по предмету, его знания оцениваются в 0 баллов и тестирование прекращается.

При 0 < t₁ £ k/2 – промежуточная ситуация, при которой необходимо, учитывая общий невысокий уровень знаний, уточнить его, используя тестовые вопросы (поскольку вопросы повышенной сложности задавать практически бесполезно). Число дополнительных тестовых вопросов принято равным k/2.

2. При k/2 < t₁ с учетом повышенного уровня знаний его уточнение целесообразно выполнять с использованием вопросов повышенной сложности. Их число также принимается равным k/2.

Получаемый алгоритм двухступенчатого тестирования проиллюстрирован на дереве опроса на рис. 2.

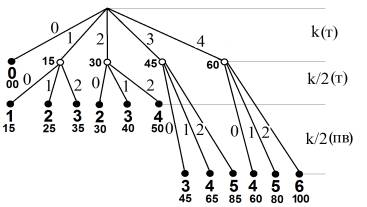
Рис. 2. Схема алгоритма 2-уровневого тестирования

Рассмотрим образное представление результатов тестирования и оценка их близости. Обозначим порядковый номер обучающегося через i, номер раздела – N, подраздела – j, число баллов, получаемое обучающимся i при проверке знаний по подразделу j раздела N – через . Число баллов лежит на отрезке [0; 100]. Геометрически – это целочисленная точка внутри данного интервала. Очевидно, для оценки общего уровня знаний в группе обучающихся необходимо сравнивать результаты тестирования обучающихся с различными порядковыми номерами по одному подразделу. Близость двух уровней знаний и предложено характеризовать модулем их разности:

.

Геометрический смысл разности r(i1, i2) – расстояние между точками и на оси N_j, соответствующей подразделу j раздела N.

Центром тяжести группы точек (центром), характеризующим пространственное положение центра точек, соответствующих уровням знаний группы обучающихся по разделу N_j, назовем среднеарифметические координат точек соответствующих точек: .

2. Дисперсия группы – это квадратичная мера рассеяния точек относительно их центра :

.

3. Среднеквадратичное отклонение (СКО) точек относительно (линейная мера рассеяния точек относительно ): .

Рассмотрим задачу оценки качества усвоения материала выделенного подраздела по полученному множеству результатов тестирования для группы из k обучающихся.

Вначале оценим среднее число баллов, которое может набрать обучающийся, не знающий учебный материал и случайно выбирающий варианты ответа. При составлении тестовых вопросов был использован выбор одного правильного ответа из 5 вариантов. В этом случае средняя вероятность правильного ответа равна 0,2. Соответственно, при этом получаем среднее значение в 20 баллов. Оценки с числом баллов от 0 до 20 назовем псевдонулевыми. Поскольку работа с данной категорией обучающихся представляет собой отдельную проблему, рекомендуется исключить ее из анализа общего уровня подготовки группы.

1. Первым преобразованием имеющейся выборки является отсечение псевдонулевых оценок. В итоге получим новое скорректированное множество результатов тестирования для группы из s обучающихся. В ней все оценки превышают значение 20.

2. Вторым преобразованием является расчет центра тяжести, дисперсии и СКО скорректированного множества результатов тестирования :

,

,

.

3. Определение нехарактерных точек (выбросов) среди скорректированного множества . В качестве доверительного принимается отрезок [,`]. Из множества исключаются все точки, не попадающие в доверительный отрезок. Итоговое множество образовано точками из , для которых выполняется условие ££.

Количество элементов в итоговом множестве обозначим через р. Исключение выбросов позволяет устранить из дальнейшего анализа:

· слишком высокие на общем фоне оценки (по ним не требуется принимать никаких мер),

· слишком малые на общем фоне оценки (по ним необходимо выявить причины низкого уровня и принимать соответствующие меры).

4. Четвертым преобразованием является расчет центра тяжести итогового множества : .

Данную величину предложено принять в качестве объективной интегральной оценки среднего уровня знаний в обучаемой группе.

Дальнейшие действия преподавателя (тьютора) зависят от того, какова принята допустимая величина среднего уровня знаний по подразделу []. Если выполняется условие ³[], то уровень знаний во всей группе принимается удовлетворительным и можно ограничиться только корректирующими действиями в обучающимися с малыми тестовыми показателями, которые выпадают из основной группы.

Если же выполняется условие <[], то уровень знаний во всей группе принимается неудовлетворительным. В этом случае необходимо проведение дополнительного корректирующего занятия во всей обучаемой группой с разъяснением тех вопросов, которые вызвали трудности при тестировании.

Проведение такого занятия чрезвычайно важно по следующей причине. Только проходя тестирование, значительная часть обучающихся выявляет те вопросы, которые не в полной мере поняты ими из основного учебного процесса. Получение низкого балла на тестировании является реальным стимулом для устранения обучающимися этих пробелов. Данную открывающуюся возможность восполнения знаний преподаватель может и должен использовать в своей работе.

В целом предлагаемая организация контента в информационно-тестирующей системе и дополнение стандартной LMS программой-анализатором позволит освободить преподавателя от большого объема рутинной работы, сделать учебный процесс более предсказуемым, динамичным и адаптивно управляемым, привить как студентам, так и преподавателям, навыки активного взаимодействия с информационными ресурсами современного уровня, органично дополняющими традиционным формам обучения. Во многом это позволит решить вопросы организации самостоятельной работы, которые довольно остро ставит перед вузами переход на учебные стандарты третьего поколения.