Н.Г. Подаева, М.В. Подаев
Елецкий государственный университет им. И.А. Бунина
обучение основам
геометрии в школе: социокультурная коммуникация и задача осознания
Резюме. Раскрываются основные линии
концепции обновления содержания обучения математике в направлении
социокультурной парадигмы. Познавательная деятельность в области математики
представлена как цикл, внутренняя динамика культурного освоения
субъектом-обучающимся ценностей, носители которых – математические категории,
объекты, методы. Раскрывается содержание этапа цикла – коммуникации – на
примере обучения основам геометрии учащихся
5-6 классов.
Ключевые слова: математическое
образование – особая форма социализации; мыследеятельностное содержание
обучения математике; ценностное отношение; коммуникация; трансляция ценности;
задача осознания.
Summary. As
part of the socio-cultural concept of education cognitive activity in
mathematics is presented as a cycle of cultural development of students values.
Their carriers - mathematical categories, objects, methods. The content of the
first stages of the cycle - the value orientation and motivation - for example,
thought-activity learning technologies based on the geometry of pupils of 5-6
classes.
Keywords:
mathematics education - a special form of socialization, thought-activity
content of teaching mathematics, value orientation, motivation.
В новых образовательных стандартах среднего (полного)
общего образования выдвигается требование сформированности понимания
выпускником метапредметных связей и универсальных учебных действий, в контексте которого выступает идея личностного развития через освоение
компетенций. Напомним, что представители философии адаптивной школы (Г.Я.
Гальперин, В.В. Давыдов, А.Н. Леонтьев, И.Я. Лернер, А.К. Маркова, В.Д.
Шадриков, Д.Б. Эльконин, и др.) содержание образования
рассматривают как социальный опыт, который усваивается конкретной личностью.
Преломляясь определенным образом через внутренний мир личности, освоенный
социальный опыт становится субъектным. В структуре такого опыта на первый план
выдвигаются мотивационно-ориентационный и креативный компоненты содержания
образования – личностные смыслы, ценностные отношения.
Такой
подход предельно
актуализирует проблему проектирования социокультурной концепции обучения математике (см. подробнее работу
[3]), в ракурсе которой выделяется в качестве ведущей категории ценность: главным содержательным
объектом в образовании выступают математические категории и методы как носители
культурных ценностей. Социокультурное
содержание учения в области математики состоит в усвоении предметных знаний,
навыков, умений как форм освоения культурных ценностей.
Нами разработана функциональная модель социокультурного
обучения математике, в процессуальном плане которой выделяются
уровни обученности, представляющие собой целостную систему поэтапного
формирования математической деятельности. Данные уровни могут быть также
описаны и как культурные базовые способности (функции мышления), и как
компоненты системы психодидактических задач: уровень понимания материала – обеспечивается
реализацией задач осознания, осмысления, обобщения материала; уровень усвоения материала: задачи
запоминания, систематизации, профилактики забывания; уровень применения (освоения): задачи
формирования умений, стандартного и творческого применения, (см. подробнее
работы [3], [4]).
Наполнением
содержательного блока является модель динамики освоения субъектом ценностей (рис.1): познавательную деятельность мы представили
как системное образование, выделяя компоненты, которые одновременно
рассматриваются и как фазы цикла культурного освоения субъектом ценностей
(носители которых – математические категории, объекты, методы), как динамика
деятельности познания – ценностная
ориентация, побуждение, коммуникация, адаптация и продуцирование.
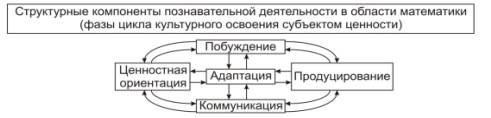
Рис. 1. Модель
динамики освоения субъектом ценности.
Ценностное отношение к
математическим категориям и методам как «принятие или отклонение объекта» [1,
с. 107] возникает на каждой фазе этого цикла, но, только пройдя все звенья,
фазы цикла, становится культурной ценностью. В работе [4] мы раскрываем
проблему формирования у школьников ценностного
отношения как принятия достаточно «скучных» положений математики в качестве
культурной ценности на примере пропедевтического курса «Основы геометрии» для
учащихся 5–6 классов. Здесь акцентировался такой этап динамики освоения
ценности, как ценностная ориентация
(или рефлексия ценности).
Остановимся подробнее на этапе коммуникации. Это звено обратной связи в структуре познавательной
деятельности, предполагающее адресность, направленность на учащегося, –
необходимо выявить статус математической информации как информации семантической
(т.е. осознанной, значимой, наполненной личностным смыслом). Анализ социологических
исследований позволил нам выделить следующие подсистемы коммуникационного
аспекта сознания: кодирование (усвоение математической терминологии и символики как
языковой формы представления информации); трансляция
(конкретизация, дезабстрагирование научной информации применительно к обучению
– методы восхождения от абстрактного к конкретному и обратно –– от моделей
геометрических понятий к их абстрактному представлению); коммутация (воспроизводство смыслов и значений предметного
материала в практической учебной деятельности).
Существенную
роль в процессе коммуникации (как
этапе динамики освоения ценности) мы отводим пониманию (как обеспечивающей его функции мышления и уровню обученности).
Другими словами, концептуальная гипотеза исследования состоит в предположении –
эффективность коммуникационных процессов
применительно к обучению положительно коррелирует с реализацией
психодидактических задач осознания, осмысления и обобщения, обеспечивающих
уровень понимания математического
материала. В дидактике выделяют три уровня обученности: понимания, усвоения и применения материала, и в системе
психодидактических задач обучения первый компонент, соответствующий уровню понимания, включает три задачи: 1 — осознания; 2 — осмысления; 3 — обобщения.
В качестве системообразующей мы выделяем задачу осознания: учащиеся, которые не осознали материал, не смогут его ни
осмыслить, ни обобщить.
Итак, первая ступень понимания соответствует задаче осознания, обеспечивающей механизмы
осуществления коммуникации в динамике освоения ценности: отнесение воспринимаемого предмета к соответствующей категории предметов,
обеспечение получения учащимся представлений — установление им соответствия
между словом и образом, оперирование образом, ориентация в пространстве. Критерием эффективности этапа коммуникации
является осознанность учебного материала – способность чётко дифференцировать
объём и содержание понятия, образно представлять словесные формулировки,
оперировать полученным образом, ориентироваться в пространстве, правильно
аргументировать действия.
Итак,
эффективность задачи осознания, обеспечивающей социокультурную коммуникацию
применительно к обучению геометрии, требует опоры на перцептивную деятельность, активизации деятельности правого
полушария – создания, оперирования образами и ориентации в пространстве. За эту
деятельность отвечает пространственное мышление, в развитых формах выступающее
как интеграция понятийного и образного. И.Я. Каплунович [2] в структуре
пространственного мышления выделяет три компонента: создание образа
(представления), оперирование им и ориентацию в пространстве. В качестве основы
развития пространственного мышления рассматривают структуру «перцепт (образ восприятия) – понятие». В связи с этим задачу осознания, играющую
существенную роль в коммуникационных процессах, целесообразно обеспечивать
через последовательность развития представлений — 1) создание перцепта (образа
восприятия), 2) оперирование образами и 3) ориентация в пространстве.
В
качестве базовых форм коммуникации применительно к обучению геометрии младших
подростков нами выбраны образовательные технологии смешанного типа, интегрирующие
традиционное обучение и новые программные средства трехмерного моделирования –
статические и динамические интерпретации с использованием технологий мультимедиа.
Трансляция информации происходит одновременно на двух кодах, что обеспечивает
включение деятельности правополушарных механизмов – «пиршество образной мысли». Опыт показывает, что при
использовании традиционных методик добиться результата мы можем лишь в случае с
самыми сильными учениками. Использование средств компьютерной анимации
обеспечивает эффективность коммуникационных процессов и позволяет даже
относительно слабым детям сформировать в своем сознании образ геометрического
объекта (или действия с ним).
Таким
образом, можно выделить схему обеспечения трансляции-коммуникации в динамике
освоения ценности применительно к обучению геометрии младших подростков:
перцепт (пространственное представление) + оперирование образами + ориентация в
пространстве = реализация закономерности осознания геометрического материала.
Оперирование остенсивными (наглядными)
образами в структуре задачи осознания геометрического материала
следует отнести к мыслительной деятельности, направленной на преобразование,
модификацию, трансформацию, видоизменение имеющихся в представлении
пространственных образов. В результате в мышлении появляются новые образы,
существенно или нет отличные от исходных. По мнению И.Я. Каплуновича, от умения
оперировать визуальными образами
зависит «успех в математической деятельности, начиная с усвоения первых
математических понятий и заканчивая решением сложных творческих задач
теоретического и прикладного характера» [2].
В
рамках данной статьи раскрываются основные линии концепции обновления содержания
обучения математике в направлении социокультурной парадигмы, квинтэссенцию
которой можно свести к следующему. Концептуальная гипотеза исследования состоит
в предположении – эффективность этапа коммуникации применительно к обучению положительно
коррелирует с реализацией психодидактической задачи осознания, обеспечивающей уровень понимания математического материала.
Литература
1. Добреньков,
В.И. Общество и образование [Текст] // В.И. Добреньков, В.Я. Нечаев. М.:
ИНФРА-М, 2003.
2. Каплунович,
И. О психологических различиях мышления двумерными и трёхмерными образами
[Текст] / И.Я. Каплунович // Вопросы психологии, 2003. № 3. С. 66-77.
3. Подаева
Н.Г. Социокультурная концепция математического образования [Текст] / Н.Г.
Подаева. – Елец: ЕГУ им. И.А. Бунина, 2012.
4. Подаева
Н.Г., Подаев М.В. Социокультурное содержание школьного математического
образования: мыследеятельностные технологии // Письма в Эмиссия.Оффлайн (The
Emissia.Offline Letters): электронный научный журнал. - Январь 2013, ART 1948 .
- CПб., 2013г. - URL: http://www.emissia.org/offline/2013/1381.htm . – Гос.рег. 0421000031. - ISSN 1997-8588. - [дата обращения
13.01.2013].
5. Шарыгин
И.Ф. Некоторые размышления по поводу школьного курса геометрии // Учительская
газета. 1992. №20. С. 14.