Физика. Физика полимеров

Баруздина О.С.

Череповецкий Государственный Университет, Россия

Современные теории структурных фазовых переходов в сегнетоэлектрических системах

Методы молекулярного моделирования в настоящее время являются общепризнанными инструментами изучения свойств веществ на уровне наноструктур. Для исследования фазовых превращений в полимерных покрытиях необходимо рассматривать молекулы, имеющие ориентационные взаимодействия.

Целью работы является изучение структурных фазовых переходов в сегнетоэлектрических полимерных системах, расчет таких макроскопических свойств как: теплоемкость, восприимчивость и сравнение полученных результатов с известной теорией.

Модель

Для описания упорядоченных систем с анизотропными ориентационными взаимодействиями применяется трехмерная решеточная модель, в каждом узле которой находится анизотропная удлиненная частица (молекула) - ротатор, обладающий только вращательными (ориентационными) степенями свободы. Модель полимерных систем можно представить в виде трехмерной кубической решетки (рис.1), которая содержит N узлов вдоль оси X, M узлов вдоль оси Y и L узлов вдоль оси Z. Положение узла характеризуются набором трех чисел i, j и k. С каждым узлом связан ротатор, его ориентация определяется сферическими углами. Потенциальная энергия взаимодействия имеет вид:

где K₁, K₂ и K₃ — константы локальных ориентационных взаимодействий дипольного типа, р - модуль дипольного момента к кинетической единицы полимерной цепи, Е-величина напряженности внешнего электрического поля.

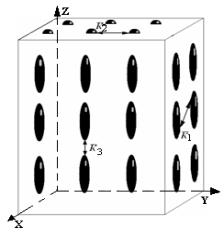
Рис.1.Модель сегнетоэлектрического кристалла

Приближение независимых узлов:

В пределе смещения при определении температуры перехода, можно показать, что вклад потенциальной энергии в теплоемкость ведет себя следующим образом: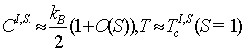

Этот результат указывает на квазигармонический характер приближения [1]. Теплоемкость имеет разрыв при Тс, величина которого стремится к нулю в пределе смещения. Приближение независимых узлов дает ряд качественных результатов, но применение этого приближения приводит к тем же неверным предсказаниям, что и теория Ландау.

Приближение независимых мод:

Приближение независимых узлов дает для критических индексов такие же значения, как и феноменологическая теория, они не согласуются с точными результатами. Приближение независимых мод ошибочно предсказывает для данной выбранной модели фазовый переход первого рода [1].

Как известно, для исследования полимерных систем неприменима теория среднего поля Ландау, так же как и не применимо приближение независимых узлов и независимых мод. Снять неопределенность позволяют результаты компьютерного моделирования.

Результаты компьютерного моделирования в отсутствии внешнего поля

Результаты моделирования показали, что в отсутствие внешнего поля (рис. 2-4),уменьшения до нуля параметра порядка, максимумы теплоемкости и восприимчивости происходят при одном и том же критическом значении параметра , что свидетельствует о существовании в рассматриваемых системах фазового перехода второго рода.

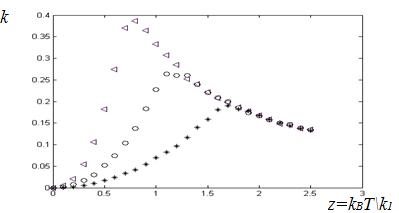
Рис. 2. Зависимости параметра дальнего ориентационного порядка от величины при значениях параметра анизотропии = 1(o), 0,5 (*), 0,2(<)

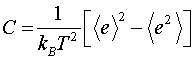Теплоемкость системы была вычислена по формуле:

где e – энергия одного звена полимерной цепи.

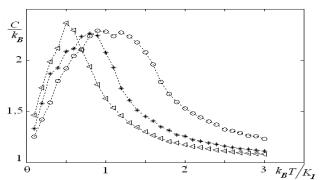
Рис.3. Зависимость теплоемкости от величины при значениях параметра анизотропии = 1(о), 0,5(*), 0,2(<);

Восприимчивость системы была вычислена по формуле:

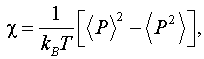
где P – модуль вектора поляризации системы.

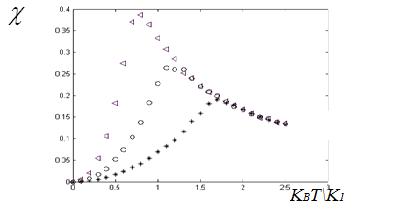
Рис.4. Зависимости диэлектрической восприимчивости от величиныПараметр анизотропии: ɛ=1(*), 0,5 (о), 0,2 (∆) .

Влияние внешнего электрического поля

Включение внешнего электрического поля приводит к увеличению температуры фазового перехода и к его размытию. На рис. 5 приведены зависимости восприимчивости полимерного сегнетоэлектрика, находящегося во внешнем электрическом поле от температуры. Расчеты проведены без учета времени релаксации (то есть считалось, что нагревание образца производилось достаточно медленно).

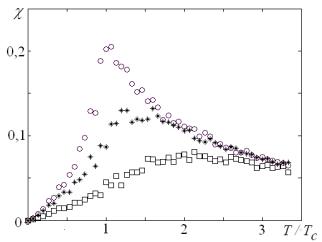
Рис.5. Зависимость восприимчивости от приведенной температуры при различных значениях величины pE /K₁ = 0 (o), 0,5 (*), 2(□) .

В феноменологической теории Ландау восприимчивость рассчитывалась как:

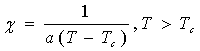
Результаты компьютерного эксперимента согласуются с теоретическими данными (1) во всех точках, кроме точки фазового перехода.

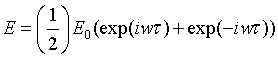Выражение для восприимчивости можно обобщить на случай, когда необходимо описать реакцию системы не зависящее от времени поле:

Тогда восприимчивость зависит от частоты и от волнового вектора. Зависящее от времени поле может передавать энергию системе, потому зависящая от частоты восприимчивость имеет как вещественную, так и мнимую части. Таким образом, была получена комплексная восприимчивость, которая имеет максимум.

Литература:

1. А.Брус, Р.Каули. Структурные фазовые переходы. Москва «Мир», 1984 год.