29.00.00
Фундаментальная физика
УДК 530.18 (УДК 530.10(075.4))
Яловенко С.Н.
Выводятся
расширенных формул теории относительности для массы, длины, времени. M(V)= M0 × [1/√(1-V2/C2)] × [1- m(V) /М чёрной] ×
[1/(1-L(V)/Lсиг)]. Показывается
относительность заряда q(V)=q0 × [1- m(V) /М чёрной)]
× [1/(1-L(V)/Lсиг)]
. Ключевые
слова: теория относительности, гравитация, электрический заряд, водоворот.
FUNDAMENTAL PHYSICS
Author Yalovenko S.
N.
Hatch the extended formulas of theory of relativity
for mass, length, time M(V)= M0 × [1/√(1-V2/C2)]
× [1- m(V) /М black] × [1/(1-L/Lwhite-fish)]. Relativity of
charge is shown q(V)=q0 × [1- m(V) /М black)] × [1/(1-L/Lwhite-fish)]
Keywords: theory of relativity, gravitation,
electric charge, whirlpool .
Продолжение
теории относительности.
Введение
Расширение преобразований лоренца
Рассмотрим две инерциальные системы отсчёта К и К’ (К’ движется относительно К со скоростью v). Направим координатные оси так, как показано на рис.1.
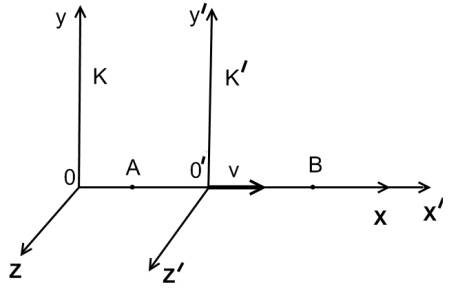
Рис.1.Движение двух инерциальных систем.
Какому-либо событию в системе К значение координат и времени, равные x, y, z, t, в системе К’ – x’, y’, z’. t. В классической физике считалось, что время в обеих системах течёт одинаково, т.е. что t=t’. Если в момент t=t’=0 начала координат обеих систем совпали, то тогда между координатами событий в обеих системах имеются следующие соотношения:
x=x’+vt’=x’+vt
y=y’
z=z’ (1)
t=t’
q=q’ или ![]()
В уравнении (1) в ведено расширение на q и назовем это уравнение расширенным преобразованием галилея. Из них вытекает закон сложения скоростей классической механики:
![]()
![]()
![]() (2)
(2)
Легко видеть, что этот закон находится в противоречии с принципом постоянства скорости света. Действительно, если в системе К' световой сигнал распространяется со скоростью C (и'х =C), то согласно (2) в системе К скорость сигнала окажется равной ux=C+V, т. е. превзойдет C. Отсюда вытекает, что преобразования Галилея должны быть заменены другими формулами. Эти формулы нетрудно найти.
Из однородности пространства следует, что формулы преобразования не должны изменяться при переносе начала координат (т. е. при замене х на х + а и т. д.). Этому условию могут удовлетворять только линейные преобразования. При указанном на рис.1. выборе координатных осей плоскость у =0 совпадает с плоскостью у'=0, а плоскость z=0 - с плоскостью z' = 0. Отсюда следует, что, например, координаты у и у' могут быть связаны только соотношением вида
![]() .
.
В силу полной равноправности систем К и К' должно также соблюдаться соотношение
![]()
с тем же значением ![]() , что и в первом случае. Перемножая оба соотношения, получим,
что
, что и в первом случае. Перемножая оба соотношения, получим,
что ![]() , откуда
, откуда ![]() . Знак плюс соответствует одинаково направленным осям у и у', знак минус — противоположно
направленным. Направив оси одинаковым образом; получим:
. Знак плюс соответствует одинаково направленным осям у и у', знак минус — противоположно
направленным. Направив оси одинаковым образом; получим:
y=y’ (3)
Такие же рассуждения приводят к формуле:
z=z’ (4)
Обратимся к нахождению преобразований для х и t. Начало координат системы К имеет координату х = 0 в системе К и х' = —Vt' в системе К'. Следовательно, при обращении х' + Vt' в нуль должна обращаться в нуль и координата х. Для этого линейное преобразование должно иметь вид:
![]() (5)
(5)
Аналогично, начало координат системы К' имеет координату х' = 0 в системе К' и х =Vt в системе К, откуда следует, что
![]() (6)
(6)
Из полного равноправия систем К и К' вытекает, что коэффициент пропорциональности в обоих случаях должен быть один и тот же (различный знак при v в этих формулах обусловлен противоположным направлением движения систем друг относительно друга — если система К' движется относительно К вправо, то система К движется относительно К' влево).
Формула (5) позволяет по известным координатам х' и времени t' события в системе К' определить координату х события в системе K. Чтобы найти формулу для определения времени t события в системе К, исключим х из уравнений (5) и (6) и разрешим получившееся выражение относительно t В результате получим:
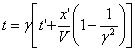 (7)
(7)
Для нахождения коэффициента
пропорциональности ![]() используем
принцип постоянства скорости света. Предположим, что в момент времени t =
t'= 0 (в обеих
системах время отсчитывается от момента, когда их начала координат совпадают)
в направлении оси х посылается импульс.
Именно в этом месте рассуждений вводим расширение представляя свет не как волну,
а как частицу обладающей импульсом и массой – виртуальной, но подверженной
гравитационному воздействию так же как и любая материальная частица с массой
используем
принцип постоянства скорости света. Предположим, что в момент времени t =
t'= 0 (в обеих
системах время отсчитывается от момента, когда их начала координат совпадают)
в направлении оси х посылается импульс.
Именно в этом месте рассуждений вводим расширение представляя свет не как волну,
а как частицу обладающей импульсом и массой – виртуальной, но подверженной
гравитационному воздействию так же как и любая материальная частица с массой ![]() , где масса находится из уравнений энергии как
, где масса находится из уравнений энергии как
![]()
E=ħν
И энергию, которую нужна затратить на преодоление гравитации этой массе m равна
![]()
То есть световой поток можно представить (упрощенно) как обмен мячиками массой m.
И так световой импульс, производит вспышку света на экране, находящемся в точке с координатой х=а. Это событие (вспышка) описывается координатами х = а, t = b в системе К и х' =а', t’ =b' в системе К', причем а = сb, а' = сb', так что координаты события в обеих системах можно представить в виде:
x=cb, t=b и x’=cb’, t’=b’
Подставив эти значения в формулы (5) и (6), получим:
cb=![]() (cb’+vb’)=
(cb’+vb’)=![]() (c+v)b’ (8)
(c+v)b’ (8)
cb’=![]() (cb - vb)=
(cb - vb)=![]() (c – v)b .
(c – v)b .
Перейдем от рассмотрения света как волны к рассмотрению света как частицы обладающей массой m .Введём расширение для уравнения (8) рассматривая свет как импульс mv ( или mc) и расширим уравнение (8) переписав его как:
mcb=γ(cb’+vb’)m’=γ(c+v)b’m’ (8.1)
mcb’=γ(cb – vb)m’=γ(c – v)bm’ .
Перемножив оба уравнения, придем к соотношению
![]()
Откуда
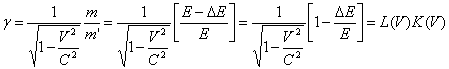 =
=![]() (9)
(9)
Где 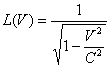 коэффициент лоренца,
коэффициент лоренца,
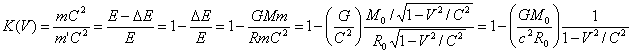
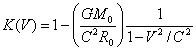
коэффициент взаимодействия, ![]() - энергия, которую
необходимо затратить кванту света на преодоление гравитационных сил. Если
М<<Мчёрной то
- энергия, которую
необходимо затратить кванту света на преодоление гравитационных сил. Если
М<<Мчёрной то ![]() и уравнение (9)
приобретает лоренцовский вид, где
и уравнение (9)
приобретает лоренцовский вид, где 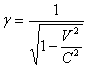 =L(V).
=L(V).
Подстановка этого значения в (5) и (7) даст окончательные формулы для х и t. Добавив к ним формулы (3) и (4), получим совокупность уравнений;
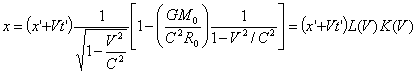 ,
,
y=y’,
(10.1)
z=z’ (10.2)
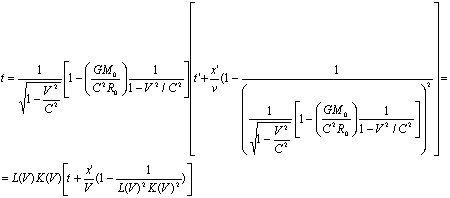 (10.3)
(10.3)
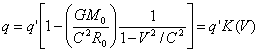
По формулам (10) осуществляется переход от координат и времени, отсчитанных в системе К', к координатам и времени в системе К. Если разрешить уравнения (10) относительно штрихованных величин, получатся формулы преобразования для перехода от системы К к системе K':
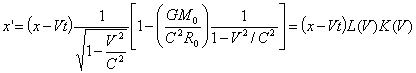 ,
,
y’=y, (11.1)
z’=z, (11.2)
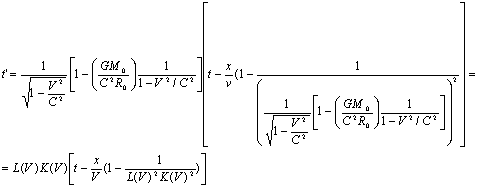 (11.3)
(11.3)
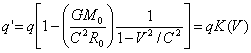
Как и следовало ожидать, учитывая
полную равноправность систем К и К', формулы (11) отличаются от
формул (10) только знаком при v. Формулы (10) и (11)
носят название р а с ш ы р е н ы х преобразований лоренца
с учётом коэффициента взаимодействия K(V).
Легко видеть, что в случае М<<Мчёрной (![]() ) преобразования переходят в преобразования лоренца, а при V<<C преобразования лоренца переходят в
преобразования Галилея (1). Таким образом, преобразования Галилея сохраняют
значение для скоростей, малых по сравнению со скоростью света. При V>C выражения
(10) и (11) для х, t,
х' и t' становятся
мнимыми. Это находится в соответствии с тем, что движение со скоростью, большей
скорости света в пустоте, невозможно. Нельзя даже пользоваться системой
отсчета, движущейся со скоростью с, так как при V=C в
знаменателях формул для х и t получается нуль.
) преобразования переходят в преобразования лоренца, а при V<<C преобразования лоренца переходят в
преобразования Галилея (1). Таким образом, преобразования Галилея сохраняют
значение для скоростей, малых по сравнению со скоростью света. При V>C выражения
(10) и (11) для х, t,
х' и t' становятся
мнимыми. Это находится в соответствии с тем, что движение со скоростью, большей
скорости света в пустоте, невозможно. Нельзя даже пользоваться системой
отсчета, движущейся со скоростью с, так как при V=C в
знаменателях формул для х и t получается нуль.
Основа теории относительность являются лоренцевы преобразования дальше все выкладки аналогичны с заменой
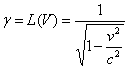
на
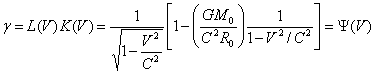 .
.
Дальше будет показана не законченность теории и необходимость введения третьего расширения.
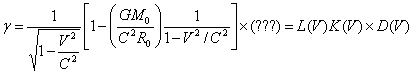 .
.
Следствия из р а с ш и р е н и я преобразований Лоренца
Из преобразований Лоренца вытекает ряд необычных с точки зрения классической механики следствий.
Одновременность событий в разных системах отсчета.
Пусть в системе К
в точках с координатами ![]() и х2
происходят одновременно два события в момент времени tl = t2 = b. Согласно
формулам (11) в
системе К' этим событиям будут соответствовать координаты
и х2
происходят одновременно два события в момент времени tl = t2 = b. Согласно
формулам (11) в
системе К' этим событиям будут соответствовать координаты
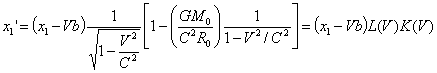 ,
,
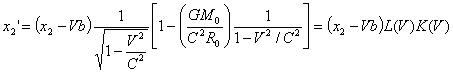
и моменты времени
![]()
![]()
![]()
Из написанных формул видно, что в случае,
если события в системе К происходят
в одном и том же месте пространства (![]() ), то они будут, совпадать в пространстве (
), то они будут, совпадать в пространстве (![]() ) и во времени (
) и во времени (![]() ) также и в системе
К'. Если же события в системе К пространственно разобщены
(
) также и в системе
К'. Если же события в системе К пространственно разобщены
(![]() ), то в системе К' они также окажутся пространственно разобщенными (
), то в системе К' они также окажутся пространственно разобщенными (![]() ), но не будут одновременными (
), но не будут одновременными (![]() ). Знак разности
). Знак разности ![]() определяется
знаком выражения
определяется
знаком выражения ![]() ; следовательно, в разных системах К' (при разных v) разность
; следовательно, в разных системах К' (при разных v) разность ![]() будет различна
по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет
предшествовать событию 2, в других системах,
наоборот, событие 2 будет предшествовать
событию 1. Заметим, что сказанное относится
лишь к событиям, между которыми
отсутствует причинная связь.
будет различна
по величине и может отличаться по знаку. Это означает, что в одних системах событие 1 будет
предшествовать событию 2, в других системах,
наоборот, событие 2 будет предшествовать
событию 1. Заметим, что сказанное относится
лишь к событиям, между которыми
отсутствует причинная связь.
Длина тел в
разных системах. Рассмотрим
стержень, расположенный вдоль оси х и покоящийся относительно системы
отсчета К' (рис.2). Длина его в этой системе равна ![]() где
где
![]() x\ и х'2 — не изменяющиеся со временем
x\ и х'2 — не изменяющиеся со временем
![]() координаты
концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его
длины в этой системе нужно отметить координаты концов стержня
координаты
концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его
длины в этой системе нужно отметить координаты концов стержня ![]() и х2
в один и тот же момент времени
и х2
в один и тот же момент времени ![]() =t2=b. Их
разность
=t2=b. Их
разность ![]() даст длину стержня,
измеренную в системе К. Чтобы найти соотношение между
даст длину стержня,
измеренную в системе К. Чтобы найти соотношение между ![]() и
и ![]() , следует взять ту из формул расширенных преобразований Лоренца, которая содержит х',
х и t, т. е.
первую из формул (11). Согласно этой формуле
, следует взять ту из формул расширенных преобразований Лоренца, которая содержит х',
х и t, т. е.
первую из формул (11). Согласно этой формуле
![]() ,
, ![]()
Откуда
![]()
Или окончательно
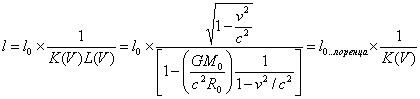 (12)
(12)
Таким образом, мы получили расширенное лоренцево преобразование для длины стержня
Если стержень длины ![]() покоится
относительно системы К, то для определения его длины в системе. К' нужно
отметить координаты концов
покоится
относительно системы К, то для определения его длины в системе. К' нужно
отметить координаты концов ![]() и х'2
в один и тот же момент времени
и х'2
в один и тот же момент времени ![]() = t'2
= b. Разность
= t'2
= b. Разность
![]() даст длину стержня в системе
даст длину стержня в системе ![]() , относительно которой он движется со скоростью v. Использовав первое из
уравнений (10), снова придем к соотношению (12).
, относительно которой он движется со скоростью v. Использовав первое из
уравнений (10), снова придем к соотношению (12).
Заметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.
Длительность
событий в разных системах. Пусть
в точке, неподвижной относительно системы К', происходит событие,
длящееся время ![]() . Началу события соответствует в этой системе
координата
. Началу события соответствует в этой системе
координата ![]() и момент
времени
и момент
времени ![]() , концу события — координата х'2 = а и
момент времени
, концу события — координата х'2 = а и
момент времени ![]() Относительно
системы К точка, в которой происходит событие, перемещается. Согласно
формулам (10) началу и концу события соответствуют в системе
Относительно
системы К точка, в которой происходит событие, перемещается. Согласно
формулам (10) началу и концу события соответствуют в системе ![]() :
:
![]() ,
,
![]()
откуда
![]()
Введя
обозначения ![]() , получим:
, получим:
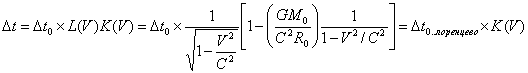 (13)
(13)
Таким образом, мы получили расширенное лоренцево преобразование для времени.
В этой формуле ![]() - длительность
события, измеренная по часам системы, движущейся с той же скоростью, что и
тело, в котором происходит процесс (тело в этой системе покоится). Иначе
"можно сказать, что
- длительность
события, измеренная по часам системы, движущейся с той же скоростью, что и
тело, в котором происходит процесс (тело в этой системе покоится). Иначе
"можно сказать, что ![]() определено по часам, движущимся вместе с
телом. Промежуток
определено по часам, движущимся вместе с
телом. Промежуток ![]() измерен по
часам системы, относительно которой тело движется со скоростью V .
измерен по
часам системы, относительно которой тело движется со скоростью V .
Время (как будет показано ниже)
напрямую связано с массой поэтому используя инвариант запишем расширенное лоренцево преобразование для массы
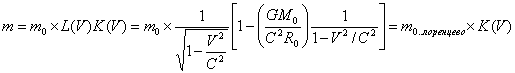 (14)
(14)
Эффект доплера. Свяжем с приемником света начало координат системы К, а с источником — начало координат системы К' (рис.2).
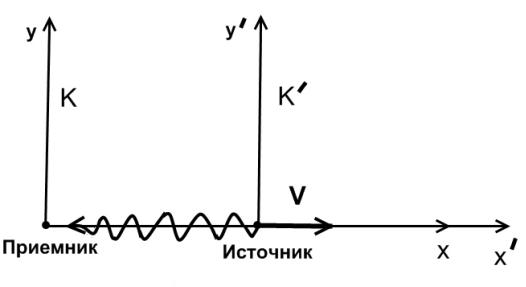
Рис.2. Движение двух инерциальных систем с излучение сигнала от одного источника к другому.
Оси х и х' направим, как обычно, вдоль вектора скорости v, с которой система К' (т. е. источник) движется относительно системы К, (т. е. приемника). Уравнение плоской световой волны, испускаемой источником по направлению к приемнику, будет в системе К' иметь вид.
![]() (15)
(15)
где ![]() — частота волны,
фиксируемая в системе отсчета, связанной с источником, т. е. частота, с
которой колеблется источник. Чтобы не ограничивать общности, мы допускаем, что
начальная фаза
— частота волны,
фиксируемая в системе отсчета, связанной с источником, т. е. частота, с
которой колеблется источник. Чтобы не ограничивать общности, мы допускаем, что
начальная фаза ![]() может быть
отлична от нуля. Мы снабдили штрихами все величины, кроме C, которая одинакова во
всех системах отсчета.
может быть
отлична от нуля. Мы снабдили штрихами все величины, кроме C, которая одинакова во
всех системах отсчета.
Согласно принципу относительности законы природы имеют одинаковый вид во всех инерциальных системах отсчета. Следовательно, в системе К волна (15) описывается уравнением:
![]() (16)
(16)
где ![]() — частота,
фиксируемая в системе отсчета К, т. е. частота, воспринимаемая
приемником.
— частота,
фиксируемая в системе отсчета К, т. е. частота, воспринимаемая
приемником.
Уравнение волны в системе К можно получить из уравнения (15), перейдя от х' и ![]() к х и t с помощью расширенных
преобразований Лоренца, Заменив в (15) х' и t’ согласно (11), получим:
к х и t с помощью расширенных
преобразований Лоренца, Заменив в (15) х' и t’ согласно (11), получим:
![]()
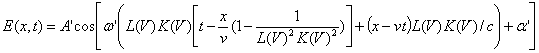
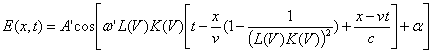 =
=
= 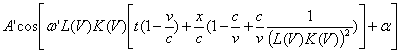 (17)
(17)
Из уравнения (17) видно, что при М<<Мчёрной ![]() и частота ω/ в
системе и в системе источника ω0
связаны как;
и частота ω/ в
системе и в системе источника ω0
связаны как;
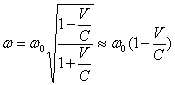 (18)
(18)
В области значений М→Мчёрной дыры и K(V)≠1 тогда K(V)→0 и частота ω' в системе и в системе источника ω0 связаны как:
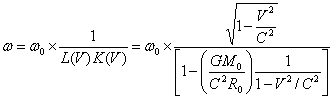 (18,1)
(18,1)
Сложение скоростей. Рассмотрим движение
материальной точки.![]() В системе К положение точки определяется в каждый
момент времени t координатами х, у,z. Выражения:
В системе К положение точки определяется в каждый
момент времени t координатами х, у,z. Выражения:
![]()
![]()
![]()
представляют собой проекции на оси х, у, z вектора
скорости точки относительно системы К. В
системе К' положение точки характеризуется каждый момент времени ![]() координатами х’,
у', z'. Проекции
на оси х’, у', z'
вектора скорости точки относительно системы К' определяются
выражениями:
координатами х’,
у', z'. Проекции
на оси х’, у', z'
вектора скорости точки относительно системы К' определяются
выражениями:
![]()
![]()
![]()
Из формулы (10) вытекает, что
![]()
![]()
![]()
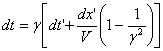
Разделим первые три равенства на четвертое, получим формулы преобразования скоростей при переходе от одной системы отсчёта к другой:
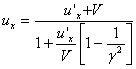
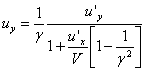 (19)
(19)
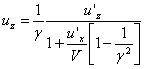
В случае, когда М<<Мчёрной то K(V)≈1 и уравнение (19) приобретает лоренцовский вид, где 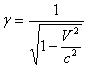 =L(V), когда V<<C, соотношение (19) переходят
в формулы сложения скоростей классической механики.
=L(V), когда V<<C, соотношение (19) переходят
в формулы сложения скоростей классической механики.
Если тело движется параллельно оси х, его скорость и относительно системы К, совпадает с их, а скорость и' относительно системы К' — с и'х. В этом случае закон сложения скоростей имеет вид:
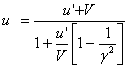 (20)
(20)
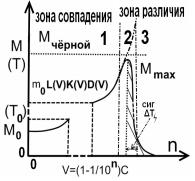
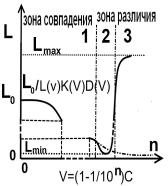
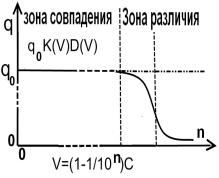
На рис.3.а показано поведение функции ![]() , на рис.3.б. поведение функции
, на рис.3.б. поведение функции ![]() , на рис 3.в.
поведение функции
, на рис 3.в.
поведение функции![]()
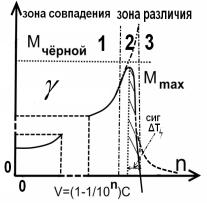
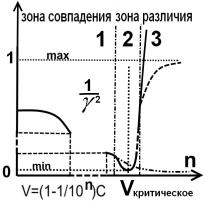
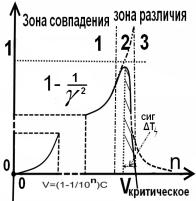
а. б. в.
Рис.3.Графики поведения функции γ для разных случаев
Из рисунков видно , что при достижении V>Vкритическое скорость u падает и меняет знак на противоположный ,
что означает сопротивление дальнейшему нарастанию скорости в нашем
представлении за счёт увеличения линейного размера тела.
Полученные формулы можно обобщить в виде:
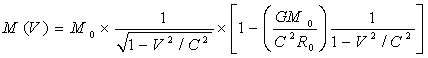 (21)
(21)
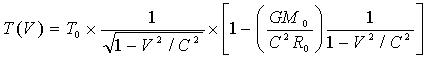 (22)
(22)
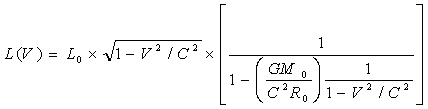 (23)
(23)
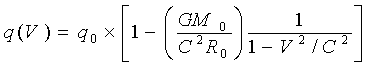
![]() (24)
(24)
а б в
Рис.4.Графики распределения для массы, времени, длины и заряда для расширенных формул теории относительности(ОТО).
Из полученных выше результатов можно построить графики для расширенного лоренцевого преобразования рис.4.а,б,в, для массы, длины, времени и что является новым для заряда (заряд тоже относителен скорости, а точнее массе). Графики построены с учетом третей составляющей D(V), которая будет выведена позже.
Литература
1.
А. Эйнштейн. А. Теория относительности. 2000
Научно-издательский центр. Регулярная и хаотическая динамика
2.
Фейнман Р., Лейтон Р.,
Сэндс М. - Фейнмановские лекции по физике.
3.
«Актуальные проблемы
современных наук-2009» №.21Материалы Международной научно-практической
конференции. Издат. «Nauka I studia;2009».ISBN 978-966-8736-05-6. Чёрный
предел. Теория относительности: новый взгляд., Яловенко С.Н., стр. 85
4.
Яловенко С.Н. Теория
относительности .Новый взгляд. Яловенко С.Н Уральский научный вестник.
Научно-теоретический и практический журнал. №5(20) 2009. ЖШС «Уралнаучкнига»
2009. ISSN 1561-6908 , Теория
относительности .Новый взгляд. стр. 33
5.
Яловенко С.Н. Чёрный
предел. Яловенко С.Н Вестник национального технического университета
"ХПИ" №8 2009г Тематический выпуск «Новые решения в современных
технологиях»; Чёрный предел. Харьков.,
2009 г. стр.81
6.
Яловенко С.Н. Чёрный
предел часть 1. Яловенко С.Н Вестник
национального технического университета "ХПИ" №43 2008г Тематический
выпуск «Новые решения в современных технологиях»; Чёрный предел часть 1 Харьков., 2008 г. стр.144
7.
Яловенко С.Н. «Чёрный предел. Теория относительности:
новый взгляд» Яловенко С.Н. ТОВ издательство «Форт» 2009г. ISBN 978-966-8599-51-4
8.
«Наука и инновации - 2010» №.13., Материалы 6
Международной научно-практической конференции.. Techniczne nauki Fizyka
.издает. «Nauka I studia;2010». Яловенко С.Н ISBN 978-966-8736-05-6. Чёрный
предел. Теория относительности: новый взгляд. Часть 5. Мировоззрение, стр. 105
9.
«Наука: Теория и
практика - 2010» №.7.Материалы 6 Международной научно-практической
конференции. издает. «Nauka I
studia;2010». Яловенко С.Н., ISBN 978-966-8736-05-6. Чёрный предел. Теория
относительности: новый взгляд, стр. 78
10. Yаlovenko S.N. Black limit. Theory of relativity. New view., Yаlovenko
S.N. Научно-теоретический и практический журнал. «Современный научный вестник №21 (77) 2009» ISSN
1561-6886 ФИЗИКА. Стр.67.
11. «Наука: Теория и практика» №.6.., Материалы 6
Международной научно-практической конференции. издает. «Nauka I
studia;2009».ISBN 978-966-8736-05-6. Yаlovenko S.N
раздел. Fizyka. Teoretyczna fizyka. Black limit.
Theory of relativity. New
view. Стр.17.
12.
«Научный прогресс на
рубеже тысячелетий - 2010»., Материалы 6 Международной научно-практической
конференции. от 27.05.2010 – 05.06.2010г. издает. Прага«Education and Science». ISBN
978-966-8736-05-6. Yаlovenko S.N Continuation of the theory of
a relativity. стр. 10.
List of the
used literature
13.
А.
Einstein. А. Theory of
relativity. 2000 Scientifically-publishing center. Regular and chaotic dynamics
Feynman Р., Лейтон Р., Sands М. - Feynman of lecture on physics..
14.
"Issues
of the day of modern sciences -2009" №.21 Materials of the International research and practice conference. Izdat. "Nauka I studia;2009".ISBN 978-966-8736-05-6. Black
limit. Theory of relativity : new look., Yаlovenko S.N., page 85
15.
Yаlovenko S.N. Theory of relativity
.New look. Yаlovenko
S.N is the Ural scientific announcer. Theoretical and practical magazine.
№5(20) 2009. ZHSHS "Уралнаучкнига" 2009. ISSN 1561-6908, Theory of relativity .New look. page 33
16. Yаlovenko S.N. Black limit. Yаlovenko S.N Announcer of national technical university of " HPI " №8 2009г the Thematic producing the "New decisions in modern technologies"; Black limit. Kharkiv., 2009 page.81
17.
Yаlovenko S.N. Black limit part 1. Yаlovenko S.N Announcer of national
technical university of " HPI " №43
2008г the Thematic
producing the "New decisions in modern technologies"; Black limit
part 1 Kharkiv., 2008 page 144
18. Yаlovenko S.N "Black limit. Theory of relativity : new look" of Yаlovenko S.N. ТОВ publishing house "Fort" 2009г. ISBN 978-966-8599-51-4
19.
"Science
and innovations - 2010" №.13., Materials 6 to the International research
and practice conference. Techniczne nauki Fizyka .publishes. "Nauka I
studia;2010". Yаlovenko
S.N ISBN 978-966-8736-05-6. Black limit. Theory of relativity : new look. Part
5. World view, page 105
20.
"Science
: is Theory and practice - 2010" №.7.Materials 6 to the International
research and practice conference. publishes. "Nauka I studia;2010". Yаlovenko S.N., ISBN
978-966-8736-05-6. Black limit. Theory of relativity : new look, page 78
21. Yаlovenko S.N. Black limit. Theory of relativity. New view., Yаlovenko S.N. Theoretical and practical magazine. "Modern scientific announcer №21(77) 2009" ISSN 1561-6886 PHYSICS. page.67.
22. "Science: Theory and practice" №.6., Materials 6 to the International research and practice conference. publishes. "Nauka I studia;2009".ISBN 978-966-8736-05-6. Yаlovenko S.N division. Fizyka. Teoretyczna fizyka. Black limit. Theory of relativity. New view. page.17.
23.
"Advance
of science on the border of millenniums - 2010"., Materials 6 to the
International research and practice conference. from 27.05.2010 - 05.06.2010г. publishes. Prague" of
Education and Science". ISBN 978-966-8736-05-6. Yаlovenko S.N Continuation of the theory of a
relativity. page 10
АНОТАЦИЯ
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
УДК
530.18 (УДК 530.10(075.4)) Яловенко С.Н. Чёрный предел. Плоская гравитация чёрной дыры
Вводится, новое ограничение – ни одно тело нельзя
разогнать до массы больше чем масса чёрной дыры, в дополнение по ограничению
скоростью света. На базе этого ограничения получаются новые формулы для теории
относительности и расширение классических уравнений для массы, длины, времени.
Показывается относительность заряда. Расширяются формулы для заряда и
гравитации. В данной работе рассматривается продолжение теории относительности
на базе развития эфирной теории, где дискретным элементом сверхтекучего эфира
является крептон (крепкая волна), элементарные частицы представлены плоскими
водоворотами, гравитация представлена как изменяющаяся плотность крептона
(крепкая волна), создающаяся плоскими водоворотами. Заряд представлен как
растянутый водоворотом хвост синусоиды не свёрнутый спиралью и созданный
дипольным смещением крептона. Энергия частиц представлена как превращение
поступательной энергии волны во вращательную энергию водоворота. Показано, что
гравитация чёрной дыры плоская, а не круг. Выведен звёздный коэффициент
преломления. Получены формулы расширения для:
M(V)=M0×[1/√(1-V2/C2)]×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L(V)/Lсиг)]
T(V)=T0×[1/√(1-V2/C2)]×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L(V)/Lсиг)]
L(V)=L0×[√(1-V2/C2)]×[1/[1-(GM0/C2R0)(1/1-V2/C2)]]×[1-L(V)/Lсиг]
q(V)=q0×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L/Lсиг)]
M(V)= M0×[1/√(1-V2/C2)]×[1-
m(V) /М чёрной]×[1/(1-L(V)/Lсиг)]
T(V)=T0×[1/√(1-V2/C2)]×[1-
m(V) /М чёрной)]×[1/(1-L(V)/Lсиг)]
L(V)=L0×[√(1-V2/C2)]×[1/(1-
m(V) /М чёрной)]×[1-L(V)/Lсиг]
q(V)=q0×[1- m(V) /М чёрной)]×[1/(1-L(V)/Lсиг)]
FЗАРЯДА(R)=[1/(R0+R)2]×[q1 q2]×SIN2((π/2)(1/(1+ΘR))×P(α,β)
EЗАРЯДА(R)=[1/(R0+R)2]×q× SIN((π/2)(1/(1+ΘR))× P(α,β)
Eгравитация(r)=[GM]×[1/((Δr)2+r2)]×P(α , β)
Eгравитация(r)=[GM]×[1/((Δr)2+(r+ƒ(r))2)]×P(α , β)
Eгравитация(r)=[GM]×[[1/(Δr)2] × ехр(-G1×r2)]×P(α , β)
Fгравитация(r)=[GMm]×[1/((Δr)2+r2)]×P(α , β)
Fгравитация(r)=[GMm]×[1/((Δr)2+(r+ƒ(r))2)]×P(α , β)
Fгравитация(r)=[GMm]×[[1/(Δr)2] × ехр(-G1×r2)]×P(α , β)
Е=m0C2=Iводоворота×ω2водоворота
nзвёздный(R)=1-[(GM)2/(C2/R)]
Cсреды(R)=Cсвета× nзвёздный(R)=
=Cсвета×[1-(GM)2/(C2/R)]=
= Cсвета×[1-(ΔRминимум/R)2]
Ключевые
слова: теория относительности,
водоворот, крептон, гравитация, плотность, масса, время, длина, заряд, скорость
света, чёрная дыра.
Э-534
ISBN 5-93972-002-1
530.1
Ф 50
UDK 530.18 (UDK 530.10(075.4)) Yalovenko S.N. the Black limit. Part 10.
Secret of times or ether theory of relativity
Entered, new limitation – not a single body can not be dispersed to mass
more than mass of black hole, in addition on limiting to velocity of light. On
the base of this limitation new formulas for the theory of relativity and
expansion of classic equalizations turn out for mass of,dliny, time. Relativity
of charge is shown. Rasshiryayutsya formulas for a
charge and gravitation. In this work continuation of theory of relativity is
examined on the base of development of ether theory, where the discrete element
of sverkhtekuchego ether is krepton (strong wave) .Gde elementary particles are
presented flat whirlpools, a gravitation is presented as a changing closeness
of kreptona (strong wave). created flat whirlpools. A charge is presented
however convolute the tail of sinewave stretched a whirlpool is in by a spiral
and created. Energy of particles is presented as converting of forward energy
of wave into rotatory energy of whirlpool. It is rotined that the gravitation
of black hole is flat, but not circle. The star coefficient of refraction is
shown out. The formulas of expansion are got for:
M(V)=M0×[1/√(1-V2/C2)]×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L/Lwhite-fish)]
T(V)=T0×[1/√(1-V2/C2)]×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L/Lwhite-fish)]
L(V)=L0×[√(1-V2/C2)]×1/[1-(GM0/C2R0)(1/1-V2/C2)]×[(1-L/Lwhite-fish)
q(V)=q0×[1-(GM0/C2R0)(1/1-V2/C2)]×[1/(1-L/Lwhite-fish)]
или
M(V)= M0×[1/√(1-V2/C2)]×[1-
m(V) /М black]×[1/(1-L/Lwhite-fish)]
T(V)=T0×[1/√(1-V2/C2)]×[1-
m(V) /М black)]×[1/(1-L/Lwhite-fish)]
L(V)=L0×[√(1-V2/C2)]×1/[1-
m(V) /М black]×[(1-L/Lwhite-fish)
q(V)=q0×[1- m(V)
/М black)]×[1/(1-L/Lwhite-fish)]
Fcharge (R)=[1/(R0+R)2]×[q1 q2]×SIN2((π/2)(1/(1+ΘR))×P(α,β)
Echarge (R)=[1/(R0+R)2]×q× SIN((π/2)(1/(1+ΘR))×
P(α,β)
Egravitations (r)=[GM]×[1/((Δr)2+r2)]×P(α
, β)
Egravitations (r)=[GM]×[1/((Δr)2+(r+ƒ(r))2)]×P(α
, β)
Egravitations (r)=[GM]×[[1/(Δr)2]
× ехр(-G1×r2)]×P(α , β)
Fgravitations (r)=[GMm]×[1/((Δr)2+r2)]×P(α
, β)
Fgravitations (r)=[GMm]×[1/((Δr)2+(r+ƒ(r))2)]×P(α
, β)
Fgravitations (r)=[GMm]×[[1/(Δr)2]
× ехр(-G1×r2)]×P(α , β)
Е=m0C2=Iwhirlpool ×ω2whirlpool
nstar (R)=1-[(GM)2/(C2/R)]
Cenvironments (R)=Clight ×
nstar (R)=
=Clight ×[1-(GM)2/(C2/R)]=
= Clight ×[1-(ΔRminimum /R)2]
Keywords: theory of relativity, whirlpool, krepton,
gravitation, closeness, mass, time, length, charge, velocity of light.