Физика/ 1. Теоретическая физика./ Теоретическая механика.
К. физ.-мат.
наук Севрюков П.Ф.
Ставропольский
государственный педагогический институт, Россия.
Введение функций наклона в
возмущённой задаче Баррара.
Рассмотрим движение
спутника, принимаемого за материальную точку, в поле тяготения осесимметричной
планеты. Если ось аппликат направить вдоль оси динамической симметрии планеты,
а начало координат поместить в произвольной точке этой оси, то гравитационный
потенциал в стандартных обозначениях будет иметь вид
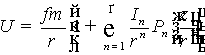 , (1)
, (1)
где f – гравитационная постоянная, т – масса планеты, r – модуль
радиус-вектора, In – постоянный
параметр, Рn – полином Лежандра n
– го порядка.
Гравитационное поле
планеты будем аппроксимировать полем тяготения Баррара [1, 3]. При этом начало
координат поместим в шаровую точку инерции планеты, тогда I1=с. Это
значение составляет аппликату центра масс планеты, I2=0, а
потенциал Баррара запишется следующим образом:
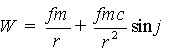 , (2)
, (2)
где sinφ=![]() . Оставшиеся
члены гравитационного потенциала составят пертурбационную функцию
. Оставшиеся
члены гравитационного потенциала составят пертурбационную функцию
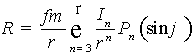 , (3)
, (3)
U=W+R. (4)
Задача Баррара
полностью учитывает возмущающий эффект второй зональной гармоники
гравитационного потенциала планеты. Уравнение движения невозмущённой задачи
Баррара интегрируется в замкнутом виде в квадратурах. [3]
В сферических
координатах r, φ, λ решение невозмущённой задачи Баррара имеет вид
![]() (5)
(5)
![]() (6)
(6)
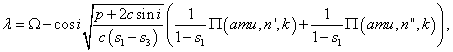 (7)
(7)
где
![]() , (8)
, (8)
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() , (11)
, (11)
![]() , (12)
, (12)
![]() . (13)
. (13)
![]() - неполные
эллиптические интегралы III рода, модуль
и параметры которых равны соответственно
- неполные
эллиптические интегралы III рода, модуль
и параметры которых равны соответственно
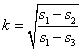 ,
, ![]() ,
, ![]() .
.
В формулах (5)-(13) а, e, i, Ω, v, ω являются аналогами большой
полуоси, эксцентриситета, наклона орбиты, долготы восходящего узла, истинной
аномалии и аргумента перицентра кеплеровской орбиты для задачи Баррара и
переходят в кеплеровские элементы про с=0.
Выражение (6) с учётом (10)
и (11), а также разложения в ряд
![]() (14)
(14)
с точностью до ɛ2 даёт
sinφ=sini∙cosƟ, (15)
где
Ɵ=v+ω. (16)
Запишем пертурбационную
функцию R в виде
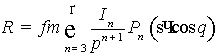 , (17)
, (17)
где для сокращения записи обозначено s=sini.
Введём функции наклона i по формуле
![]()
![]() , (18)
, (18)
тогда
![]() . (19)
. (19)
При вычислении
интеграла (18) воспользуемся теоремой сложения для полиномов Лежандра:
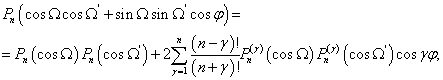 (20)
(20)
где ![]() - присоединённые
функции Лежандра.
- присоединённые
функции Лежандра.
Положив в формуле (20) ![]()
![]() ,
, ![]() ,
, ![]() , будем иметь
, будем иметь
![]() , (21)
, (21)
где s=sini,
α=cosi.
Умножим обе части
равенства (21) на cosγθ и
проинтегрируем по θ в пределах
от 0 до 2π.
При γ>n
![]() , (22)
, (22)
а при γ≤n
![]() . (23)
. (23)
Таким образом, функции
наклона ![]() выразились через присоединённые функции
Лежандра:
выразились через присоединённые функции
Лежандра:
![]() . (24)
. (24)
Отметим, что функции
наклона ![]() могут обращаться в нуль. Этот факт вытекает
из свойств присоединённых функций Лежандра. Поскольку
могут обращаться в нуль. Этот факт вытекает
из свойств присоединённых функций Лежандра. Поскольку
![]() ,
,
![]() ,
, ![]() .
.
Поэтому при нечётном п+γ
![]() .
.
Вернёмся теперь к
пертурбационной функции R и выразим её через функции наклона ![]() и эксцентриситета
и эксцентриситета ![]() , где
, где
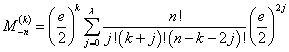 , (25)
, (25)
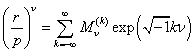 . (26)
. (26)
Подставляя в формулу
(17) выражения (19) и (26), получим
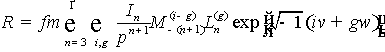 , (27)
, (27)
где положено j=k+γ.
Разложение пертурбационной
функции вида (27) может быть с успехом использовано в задачах теории
возмущений.
Библиографический список.
1.
Barrar R.B. Some remarks on the motion of a satellite of an oblate
planet.// Astron. Journ. 1961. V. 66, №1.
2.
Дёмин В.Г. Движение
искусственного спутника в нецентральном поле тяготения./ М.: Наука, 1968. стр.
122-130.
3.
Конкс В.Я. Канонические
переменные «действие-угол» в задаче Баррара. //Космические исследования, 1985,
т. 23, вып. 3, стр.477-479.
4.
Севрюков П.Ф. О
дополнительных аналитических первых интегралах возмущённой задачи Баррара.//
Проблемы механики управляемого движения. Нелинейные динамические системы:
Межвуз. сб. научн. трудов/ Пермь: – Перм. ун-т, 1989. стр. 142-145.
5.
Севрюков П.Ф. Введение
функций эксцентриситета в возмущённой задаче Баррара.// Materialy VII Miҿdzynarowej na-ujwi-praktycznej konferencji
«Perpektywiczne opracowania sa nauka i technikami» -2012. Volume 17/ Chemia I
chemiczne nechnologie. Fizyka: Przemyṡl. Nauka i studia. p. 52-57.