РАДИОФИЗИКА
к. ф- м.н. Антонов В. В., д.т.н. Димитрюк А.А.
Саратовский
государственный технический университет, Россия
Эффективный умножитель частоты
СВЧ излучения миллиметрового диапазона на основе пинч-эффекта
Преобразование
частоты СВЧ излучения в плазменных умножителях часто-ты определяется характером
взаимодействия электромагнитного поля с плазмой. Теоретический анализ такого
взаимодействия основан на решении уравнений Максвелла совместно с уравнениями
движения и непрерывности. Общее рассмотрение
данных уравнений позволяет выделить ряд нелинейных механизмов взаимодействия электромагнитных волн с
плазмой, ответственных за генерацию гармоник, в которых ведущее место занимают
эффекты зависи-мости концентрации носителей заряда от координаты и
напряженности электрического поля [1]. В работах [2]-[3], показано, что в
слабонеоднородной среде возникает генерация второй гармоники при условии плазменного резонанса. Коэффициент
трансформации первой гармоники во вторую может достигать значительной величины
при достаточно малой амплитуде электромагнитного излучения. Коэффициент
умножения частоты существенно зависит от степени неоднородности концентрации плазмы.
Основной особенностью работ по исследованию умножителей частоты на неоднородной
плазме является условие плазменного резонанса, необходимого для эффективной
работы устройств. В газоразрядной плазме плазменные частоты соответствуют сантиметровому
диапазону длин волн и, эффективность работы умножителей частоты в
миллиметровом и субмиллиметровом диапазонах будет незначительной.
Создание в полупроводнике значительной управляемой концентра-ционной
неоднородности внешними электрическим и магнитным полями позволяет значительно
увеличить эффективность преобразования частот СВЧ излучения в миллиметровом и субмиллиметровом
диапазонах.
Процесс взаимодействия
электромагнитного излучения частоты ![]() с прямоугольной
пластиной антимонида индия определяется совместным реше-нием уравнений
Максвелла, движения и непрерывности:
с прямоугольной
пластиной антимонида индия определяется совместным реше-нием уравнений
Максвелла, движения и непрерывности:
![]() (1)
(1) 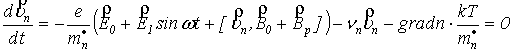 , (2)
, (2) 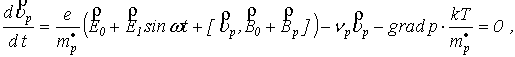 (3)
(3)
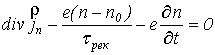 ,
(4)
,
(4)
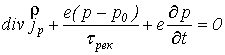 ,
(5)
,
(5)
где
H![]() - напряженность сжимающего магнитного поля тока;
- напряженность сжимающего магнитного поля тока;![]() и
и ![]() - плотности электрического тока электронов и дырок,
протекающие в намагниченном полу-проводнике под действием постоянного и
переменного электрических полей;
- плотности электрического тока электронов и дырок,
протекающие в намагниченном полу-проводнике под действием постоянного и
переменного электрических полей;![]() -диэлектрическая проницаемость решетки полупроводника;
-диэлектрическая проницаемость решетки полупроводника; ![]() -циклическая
частота электромагнитного поля;
-циклическая
частота электромагнитного поля;![]() -скорости движения электронов и дырок;
-скорости движения электронов и дырок; ![]() и
и ![]() напряженности
постоянного и переменного электрических полей;
напряженности
постоянного и переменного электрических полей; ![]() и
и ![]() -индукции внешнего постоянного и собственного сжимающего
магнитных полей;
-индукции внешнего постоянного и собственного сжимающего
магнитных полей;![]() -частоты столкновений электронов и дырок с узлами решетки; n и р - локальные
концентрации электронов и дырок;
-частоты столкновений электронов и дырок с узлами решетки; n и р - локальные
концентрации электронов и дырок; ![]() -эффективные массы носителей заряда; Т-температура
решетки;
-эффективные массы носителей заряда; Т-температура
решетки; ![]() -равновесные концентрации электронов и дырок,
-равновесные концентрации электронов и дырок, ![]() -время рекомбинации неравновесных электронов и дырок [ 4
].
-время рекомбинации неравновесных электронов и дырок [ 4
].
Решение системы уравнений получим при ориентации векторов
напряженностей постоянного и
переменного электрических полей вдоль оси x и
постоянного внешнего магнитного поля вдоль оси y. Размер полупроводниковой пластины вдоль оси z значительно меньше ее
других размеров. Данное предположение дает
возможность учесть только
составляющую собственного сжимающего магнитного поля вдоль оси y, создаваемого
током, протекающим через образец. Разогрев носителей заряда и изменение
подвижности как функции концентрации не учитывается, так как пинч-эффект
наблюдается при полях порядка 200-300 В/см.
Преобразуем
уравнения (2)-(3) к следующему уравнению для определения проекции вектора скорости вдоль оси x:![]()
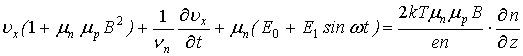 . (4)
. (4)
Оценим вклад нелинейного члена ![]() по индукции
сжимающего магнитного поля
по индукции
сжимающего магнитного поля ![]() , входящего в уравнение (4). Интегрируя уравнение (1) по
сечению образца S=d-L , где d -
размер пластины по оси сжатия z, L - длина пластины по оси y , получаем
, входящего в уравнение (4). Интегрируя уравнение (1) по
сечению образца S=d-L , где d -
размер пластины по оси сжатия z, L - длина пластины по оси y , получаем
![]() ,
,
где
![]() - сила постоянного электрического тока, создающего
собственное сжимающее магнитное поле. При выборе
параметров размеров пластины, соответствующих стандартному сечению волноводов
диапазонов 8 мм и 2 мм, получаем неравенство
- сила постоянного электрического тока, создающего
собственное сжимающее магнитное поле. При выборе
параметров размеров пластины, соответствующих стандартному сечению волноводов
диапазонов 8 мм и 2 мм, получаем неравенство ![]()
Проведем
оценку диффузионного члена, входящего в уравнение (4), используя критерий
Беннета:![]() . Дифференцируя данное уравнение по координате z , получаем неравенство:
. Дифференцируя данное уравнение по координате z , получаем неравенство: ![]()
Из
последнего неравенства следует условие малости диффузионного члена в правой
части уравнении (4) по сравнению с полевым членом ![]() . Используя данное условие, получаем дифференциальное
уравнение для определения x проекции скорости, решение которого имеет вид:
. Используя данное условие, получаем дифференциальное
уравнение для определения x проекции скорости, решение которого имеет вид:
![]() (5)
(5)
где
![]() ,
, ![]() ,
,
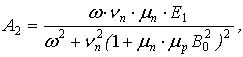
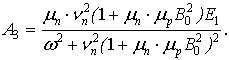
Частота столкновений электронов с узлами решетки ![]() с
с![]() , так что
, так что
![]()
![]() 0. Учитывая все приближения, получаем
систему уравнений для определения напряженности сжимающего магнитного
поля и концентрации носителей заряда
0. Учитывая все приближения, получаем
систему уравнений для определения напряженности сжимающего магнитного
поля и концентрации носителей заряда
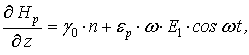 (6)
(6)
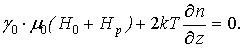 (7)
(7)
В уравнениях (6)-(7) введено обозначение ![]() . Соответствующие оценки токов проводимости и смещения в миллиметровом и субмиллиметровом
диапазонах показали, что плотность тока проводимости электронов и дырок
значительно больше модуля тока смещения. Следовательно, систему уравнений (6)-(7) можно преобразовать в
дифференциальное уравнение второго порядка относительно напряженности
сжимающего магнитного поля
. Соответствующие оценки токов проводимости и смещения в миллиметровом и субмиллиметровом
диапазонах показали, что плотность тока проводимости электронов и дырок
значительно больше модуля тока смещения. Следовательно, систему уравнений (6)-(7) можно преобразовать в
дифференциальное уравнение второго порядка относительно напряженности
сжимающего магнитного поля ![]() :
:
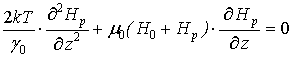 . (8)
. (8)
Решение данного нелинейного уравнения получаем с учетом
замены переменной ![]() :
:
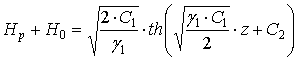 ,
(9)
,
(9)
где ![]() . Постоянные интегрирования С
. Постоянные интегрирования С![]() и С
и С![]() определяются из граничных условий:
определяются из граничных условий:
![]() ,
(10)
,
(10) 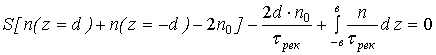 ,
(11)
,
(11)
где S –скорость
поверхностной рекомбинации.
Функциональная зависимость концентрации от координаты,
времени и напряженностей электрических и магнитных полей имеет вид
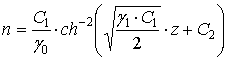 . (12)
. (12)
Из граничных условий (10)-(11) позволяют
определяем постоянные интегрирования С![]() и С
и С![]() в различные промежутки времени t. Для упрощения расчетов
трансцендентных уравнений (10)-(11), введем эффективное электри-ческое поле
в различные промежутки времени t. Для упрощения расчетов
трансцендентных уравнений (10)-(11), введем эффективное электри-ческое поле ![]() , зависящее от времени t:
, зависящее от времени t:
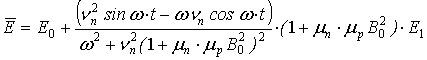 ,
,
относительно которого определим зависимости ![]() и
и ![]() от времени и напря-женностей электрического суммарного поля. Функциональные зависимости
от времени и напря-женностей электрического суммарного поля. Функциональные зависимости ![]() и
и ![]() от приведенного поля
от приведенного поля ![]() получаем из системы
(10)-(11) . Сила Холла сдвигает максимум распределения концентрации к одной из граней образца. Положение
максимума зависит от постоянной
интегрирования,
получаем из системы
(10)-(11) . Сила Холла сдвигает максимум распределения концентрации к одной из граней образца. Положение
максимума зависит от постоянной
интегрирования, ![]() которая также
существенно зависит от индукции
магнитного поля.
которая также
существенно зависит от индукции
магнитного поля.
Система уравнений (10)-(11) может быть решена
только численными методами. Полученные решения позволяют построить зависимости ![]() и
и ![]() от эффективного
электрического поля и постоянного магнитного поля. Из решения уравнения (11)
следует линейность вольтамперной характеристики (ВАХ) при малых значениях
аргумента гиперболических функций. Неоднородное распределение носителей заряда
при этом
отсутствует. Увеличение аргумента приводит при одном
значении электрического поля
от эффективного
электрического поля и постоянного магнитного поля. Из решения уравнения (11)
следует линейность вольтамперной характеристики (ВАХ) при малых значениях
аргумента гиперболических функций. Неоднородное распределение носителей заряда
при этом
отсутствует. Увеличение аргумента приводит при одном
значении электрического поля ![]() к появлению трех решений. Проведенные количественные оценки решения
системы уравнений (10)-(11) относительно постоянных
к появлению трех решений. Проведенные количественные оценки решения
системы уравнений (10)-(11) относительно постоянных ![]() и
и ![]() , позволяют получить трехзначную функцию относительно
независимой переменной
, позволяют получить трехзначную функцию относительно
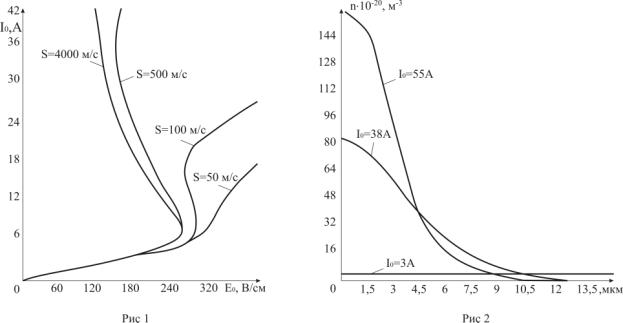
независимой переменной ![]() . На рис.1 приведена
зависимость тока I от
напряженности постоянного электрического поля
. На рис.1 приведена
зависимость тока I от
напряженности постоянного электрического поля ![]() (вольтамперная характеристика) при различных значениях
скорости поверхностной рекомбинации
(вольтамперная характеристика) при различных значениях
скорости поверхностной рекомбинации ![]() . Линейный участок полученной функции определяет линейную
вольтамперную характеристику. Ширина области отрицательной дифференциальной
проводимости (ОДП) существенно зависит от скорости поверхностной рекомбинации S. Расчет проведен для n-InSB c
. Линейный участок полученной функции определяет линейную
вольтамперную характеристику. Ширина области отрицательной дифференциальной
проводимости (ОДП) существенно зависит от скорости поверхностной рекомбинации S. Расчет проведен для n-InSB c ![]() см
см![]() ;
;![]()
![]() см/c
см/c![]() ; 2d=30 мкм. Образование S-образной ВАХ и наличие большого градиента
концентрации дают возможность рассчитывать на значительную нелинейность
рассматриваемого взаимодействия.
; 2d=30 мкм. Образование S-образной ВАХ и наличие большого градиента
концентрации дают возможность рассчитывать на значительную нелинейность
рассматриваемого взаимодействия.
 Постоянная интегрирования
Постоянная интегрирования ![]() аппроксимируется
функцией
аппроксимируется
функцией ![]() на нелинейном
участке. При малых значениях скорости поверхностной рекомбинации S функция
на нелинейном
участке. При малых значениях скорости поверхностной рекомбинации S функция ![]() будет монотонно
возрастающей при увеличении эффективной напряженности электрического поля
будет монотонно
возрастающей при увеличении эффективной напряженности электрического поля ![]() . Зависимости концентрации от координаты z при различных значениях
тока, протекающего через полупроводниковую пластину в области
отрицательной дифферен-циальной
проводимости, приведены на рис.2 .
. Зависимости концентрации от координаты z при различных значениях
тока, протекающего через полупроводниковую пластину в области
отрицательной дифферен-циальной
проводимости, приведены на рис.2 .
Для определения спектрального состава плотности
тока, разложим ее в ряд Фурье:
![]() ,
(13)
,
(13)
Коэффициенты в разложении определяются интегралами
![]() . (14)
. (14)
Введем обозначения ![]() и выразим плотность
тока через суммы синусов:
и выразим плотность
тока через суммы синусов: ![]() =
=![]() Значения
Значения ![]() и
и ![]() определяются через
коэффициенты разложения (14) следующим образом:
определяются через
коэффициенты разложения (14) следующим образом:
![]() .
.
Для расчета мощности, излучаемой на второй гармонике
необходимо определить сопротивление излучения на частоте 2![]() . Расчет данной величины для плазменного слоя в волноводном
тракте представляет сложную задачу. В связи с этим, для качественного анализа
величины коэффициента преобразования мощности
. Расчет данной величины для плазменного слоя в волноводном
тракте представляет сложную задачу. В связи с этим, для качественного анализа
величины коэффициента преобразования мощности ![]() , рассмотрим отношение модуля тока второй гармоники к модулю тока
первой гармоник:
, рассмотрим отношение модуля тока второй гармоники к модулю тока
первой гармоник:
![]() . (15)
. (15)
Выбор такого определения коэффициента умножением связан с
возбуждением потока высокочастотной энергии в волноводном тракте плотностью
тока. На основе выражений для коэффициента второй гармоники из разложения (13)
проведен расчет модуля плотности тока второй гармоники. Эффективность умножения
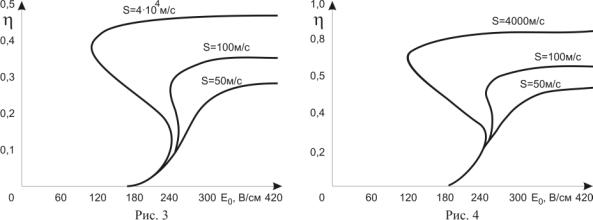
частоты определим из соотношения (15). Соответствующие кривые зависимости коэффициента
преобразования мощности ![]() от постоянного
электрического поля и различных значениях скорости поверхностной рекомбинации S представлены на рис.3 и
рис.4. Расчет проведен для следующих параметров полупроводникового материала
антимонида индия электронного типа:
от постоянного
электрического поля и различных значениях скорости поверхностной рекомбинации S представлены на рис.3 и
рис.4. Расчет проведен для следующих параметров полупроводникового материала
антимонида индия электронного типа: ![]() =65 м
=65 м![]() /В∙с;
/В∙с; ![]() =1 м
=1 м![]() /В∙с; 2d
=30 мкм;
/В∙с; 2d
=30 мкм; ![]() =10
=10![]() м
м![]() ;
;![]() =2 мм;
=2 мм; ![]() =10
=10![]() с. На рис.3 приведена графическая зависимость модуля коэффициента
с. На рис.3 приведена графическая зависимость модуля коэффициента
![]() от постоянного
электрического поля при значении амплитуды СВЧ поля Е
от постоянного
электрического поля при значении амплитуды СВЧ поля Е![]() = 20 В/см. Аналогичные зависимости при напряженности СВЧ
поля
= 20 В/см. Аналогичные зависимости при напряженности СВЧ
поля ![]() = 100 В/см приведены на рис. 4.
= 100 В/см приведены на рис. 4.
Максимальное значение коэффициента
преобразования мощности ![]() достигается в области
отрицательной дифференциальной проводимости, которая возникает при
пинч-эффекте. При значении скорости поверхностной рекомбинации, равной 50 м/с
коэффициент умножения частоты будет монотонно возрастать с ростом напряженности
электрического поля. Так как внешнее магнитное поле
достигается в области
отрицательной дифференциальной проводимости, которая возникает при
пинч-эффекте. При значении скорости поверхностной рекомбинации, равной 50 м/с
коэффициент умножения частоты будет монотонно возрастать с ростом напряженности
электрического поля. Так как внешнее магнитное поле ![]()
![]() уменьшает проекцию
тока, создающего сжатие носителей заряда и, следовательно, и препятствует образованию
пинч-эффекта, то расчет
проведен при значении
уменьшает проекцию
тока, создающего сжатие носителей заряда и, следовательно, и препятствует образованию
пинч-эффекта, то расчет
проведен при значении![]() =0.
=0.
. При большой скорости поверхностной рекомбинации
коэффициент умножения частоты
стремится к единице.
СПИСОК ЛИТЕРАТУРЫ
1. Брандт А.А., Тихомиров Ю.В. Плазменные умножители
частоты. М.: Наука, 1974. 207с.
2. Ерохин Н.С., Захаров В.Е. Генерация второй гармоники при
падении электромагнитной волны на неоднородную
плазму.// Наука, ЖЭТФ, 1969,т.56,вып.1,с. 179-185.
3. Ерохин Н.С., Моисеев С.С. Вопросы теории линейной и нелинейной трансформации волн // Наука,
Успехи физических наук, 1973,т.109, вып.2, с.225-258.
4.
Владимиров, В.В. Плазма полупроводников. М.: Атомиздат,1979.254 с.