Строительство и архитектура / 7. Водоснабжение и канализация

К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н.

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

Модель процесса размыва перед препятствием типа мостовой опоры. Общие закономерности вихревых образований перед обтекаемым цилиндром.

Если применить закон сохранения энергии, то есть считать, что все особенности перед обтекаемым телом обусловлены энергией набегающего потока, то возможно в первом приближении представить, что в потоке со сдвигом, обтекающем цилиндр, кинетическая энергия набегающего потока в прямоугольнике, ширина которого равна диаметру цилиндра, а высота – некоторому расстоянию от дна, полностью превращается в кинетическую энергию вихрей. Поэтому чем больше величина скорости набегающего потока, тем больше кинетическая энергия вихрей; от градиента скорости по глубине зависит величина (она также влияет на энергию вихря).

Кинетическая энергия выделенной части набегающего потока равна

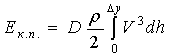, (1)

где - диаметр цилиндра.

Нами для простоты изложения рассматривается случай «почти прямолинейного» вихря, когда

, (2)

где - радиус образовавшегося вначале в осевой плоскости вихря и тут же перешедшего в подковообразный.

Кинетическая энергия вихря, представленная как энергия твердого стержня равна

(3)

где - радиус вихря, - угловая скорость его вращения как твердого стержня, - длина вихря, плотность жидкости.

Зависимость (3) наиболее точно описывает энергию вихря в самый начальный момент его зарождения – это связано с тем, что вихрь на самом деле является вихрестоком.

Для дальнейшего определения параметров вихря необходимо приравнять (1) и (3)

(4)

После своего образования вихрь начинает двигаться со скоростью, самоиндуцированной им; она равна [1]

(5)

Движущийся вихрь индуцирует в окружающем пространстве поля скоростей – поэтому поток перед цилиндром вследствие движущихся вихрей нестационарный.

После того, как вихрь образовался, есть следующие варианты его дальнейшего существования:

1. В некоторый момент он внезапно полностью разрушается.

2. Вихрь дифференцирует из-за вязкости жидкости.

3. Он постепенно теряет свою энергию за счет укоса массы и обмена с окружающей жидкостью.

В последующем изложении принимается во внимание последний случай. Принимая во внимание (4) получим равенство

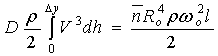, (6)

где - начальный радиус вихря, - его начальная угловая скорость.

В последнем уравнении несколько неизвестных: - длина вихря, - его радиус, - угловая скорость и для решения (6) необходимо применить дополнительные условия или уравнения.

В любой точке в пределах вихря вектор скорости складывается из составляющих , и . Модуль этого вектора следует считать величиной скорости, приводящей к размыву. Если предполагать, что , а изменяется от 0 до (в боковом сечении цилиндра), то можно было ожидать начало размыва у поверхности цилиндра в боковом сечении ( при ); из опытов де следует, что размыв начинается при меньших углах. Это можно объяснить тем, что угловая скорость меняется по длине вихря.

При построении модели не учитывалось перемещение частиц наносив, на что затрачивается некоторая энергия.

Ранее нами при определении кинетической энергии потока, переходящей в энергию вихря, брался интеграл по некоторой площади (части миделевого сечения); но известно, что потери механической энергии при заданной площади мидиевого сечения неодинаковы для тех различий в плане форм и кроме того на данной площади может быть не один вихрь, а несколько.

Из формулы [2]

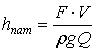, (7)

где - удельные потери механической энергии, имеющие смысл местных потерь при обтекании потоком препятствия, - сила, действующая на препятствия, - скорость набегающего потока, - общий расход потока, следует, что потери (и, возможно, та часть их, которая превращается в энергию вихря) зависят от общего коэффициента сопротивления выступа .

Величину кинетической энергии на данной и фиксированной площади миделевого сечения, перешедшей в энергию вихря возможно определить как произведение

,

Причем функция монотонна – с увеличением она увеличивается, с уменьшением уменьшается.

Если дно перед опорой размываемое и происходит размыв, то на перемещение частиц грунта затрачивается часть механической энергии потока, которая в тепло не переходит, но теряется необратимо. Энергия на перемещение частиц грунта является частью величины в (7). Следовательно, общие потери энергии при обтекании препятствия в процессе размыва можно представить как сумму

, (8)

где - потери на местные сопротивления, переходящие в тепло, - энергия, перешедшая в вихревые образования, - потери энергии на перемещение частиц грунта.

С учетам сделанных замечаний, возможно выполнить оценку величины времени образования ямы размыва: произведение есть теряемая энергия за единицу времени – если подсчитать работу, требующуюся на подъем массы грунта из ямы до уровня дна и приравнять ее величин , то время размыва будет порядка величины

(9)

Эта оценка, конечно, слишком грубая, чтобы принять ее на практике.

Заметим, что трансформация первоначальной модели в процессе построений представлений о вихревых образованиях не произошло, то есть существование вихрей не противоречит струйчатой модели с непрерывной структурой непосредственно перед цилиндром.

Известно [1], что ядро вихря индуцирует в окружающем пространстве поля скоростей и, кроме того, в данном случае вихри не могут располагаться вплотную друг к другу из-за одинакового направления вращения.

Следовательно, если вихрь движется вдоль поверхности опоры, то индуцирует такие скорости, что лишь на некотором расстоянии от него может зародиться следующий вихрь, то есть он зарождается тогда, когда предыдущий перестает быть ему помехой. Именно в этот момент в данной точке на основании вихревой модели и представляем вихрь, как будто он единственный и первый.

Поэтому трансформации модели не происходит, то есть вихревая модель не исключает первоначально предполагаемую струйчатую модель.

Литература:

1. Милн-Томсон Л.М. Теоретическая гидродинамика. М.: Мир, 1964, 655с.

2. Калякин А.М. Модель процесса размыва перед препятствием типа мостовой опоры на основе представлений о вихре. // Совершенствование методов гидравлических расчетов водопропускных и очистных сооружений: межвуз. науч. сб. Саратов: Сарат. гос. техн. ун-т, 1997. С. 33-43.