К.т.н. Антоненко Н.С., к.т.н. Петров С.В., Фатеев А.В.

 

Украинская инженерно-педагогическая  академия, Харьков, Украина

 

Оценка качества планов проведения технологических

циклов производства посредством стохастических сетей Петри с использованием метода имитационного

моделирования

 

Процесс управления конкретным технологическим процессом можно представить как временную последовательность технологических циклов производства (ТЦП). Каждый ТЦП содержит всю необходимую совокупность операций, которые выполняются рабочим персоналом. Каждая операция привязана ко времени выполнения ("временному окну") и рабочему месту оператора (заданному оборудованию, средству). При формировании технологических графиков управления и плана работы предприятия (цеха, участка и т.п.) продолжительности всех операций считаются детерминированными. Исходя из этого, рассчитываются и временные параметры сетевого графика. В то же время, продолжительности многих операций (особенно тех, выполнение которых связано с действиями персонала, либо с вероятностным характером функционирования оборудования и аппаратуры)  представ­ляют собой случайные величины, распределенные по некото­рому закону. Поэтому необходимо произвести переход от детермини­рованной сетевой модели к рассмотрению стохастической сетевой модели процесса выполнения ТЦП, что можно достичь построением модели в виде одной из разновидности стохастических сетей Петри (СП).

В стохастических сетевых моделях длительности всех операций (работ)  представляют собой случайные величины, распределенные по некоторому закону (как правило, это одно из следующих распределений: равномерное, нормальное, экспоненциальное,  b-распределение).

Используя значения математического ожидания  и дисперсии  времени выполнения каждой операции, и полагая случайные длительности операций в каждом пути независимыми, можно рассчитать математическое ожидание   и дисперсию   каждого пути сетевой модели путем простого суммирования соответственно математических ожиданий и дисперсий длительностей операций данного пути. Опираясь на центральную предельную теорему теории вероятностей, обычно предполагают, что длительности путей подчинены нормальному закону (это предположение справедливо, если число работ, входящих в путь, достаточно велико). Тем самым при знании  и  полностью определяются вероятностные характеристики пути.

Знание вероятностных характеристик каждого пути в сетевой модели плана ТЦП в общем случае не дает возможности определить вероятностные характеристики и другие параметры сетевого плана, так как действие вероятностного механизма таково, что любой путь может оказаться критическим с большей или меньшей вероятностью.

В настоящее время для определения характеристик стохастического сетевого плана проведения ТЦП используется приближенный аналитический  метод [1]. Этот метод предполагает нахождение вероятностных характеристик при расчете стохастического сетевого плана ТЦП производить в виде детерми­нированной модели, в которой в качестве длительностей операций и путей выступают соответствующие математические ожидания. Соответственно, за условно критический путь принимается путь, у которого математическое ожидание максимально. Далее, так как дисперсия этого пути известна, возможно рассчитать вероятность непревышения длительности данного пути  величины заданного срока .

Поскольку в действительности критический путь может не совпадать с путем, для которого математическое ожидание максимально, величина  дает лишь некоторую оценку вероятности того, что критический путь не превысит заданный срок. Эта оценка позволяет исключить из рассмотрения явно неприемлемые планы. Однако, при оптимизации плана ТЦП по критерию оптимального быстродействия данная оценка может оказаться слишком грубой, в особенности, если существует несколько путей близких к критическому по значению математического ожидания или (и) превосходящих по значению дисперсии, и, естественно, не может быть использована при расчете эффективности того или иного технологического процесса. 

Пусть для выполнения какого-либо ТЦП (момент ) требуется окончание некоторого множества операций, которое при составлении оптимального по быстродействию плана удалось представить в виде  параллельно выполняемых технологических цепочек .  Моменты  окончания выполнения этих цепочек  независимы и имеют плотности . Тогда случайная величина  будет иметь следующую функцию распределения:

,

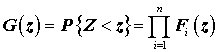где     .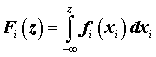

Дифференцируя, получаем сумму произведений производных отдельных функций распределения  на произведения всех остальных функций, кроме той, которая продифференцирована. Таким образом, плотность распределения случайной величины  можно записать в виде:

.

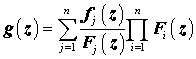Математическое ожидание случайной величины :

.

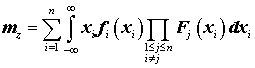Дисперсия   , где .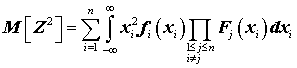

Приведенные выражения можно применить для более строгого аналитического решения задачи  определения характеристик стохастического сетевого плана проведения ТЦП. Но их применение требует наличия определенных условий, основными из которых являются: независимость операций в различных технологических цепочках, возможность получения точных функций распределения (плотности) вероятностей каждой технологической цепочки.

Таким образом, применение аналитического аппарата в качестве точного инструмента исследования стохастических сетевых моделей ТЦП нецелесообразно и достаточно сложно, с одной стороны, в силу специфики  самого процесса проведения ТЦП (большое число параметров и критериев оценки), а с другой стороны – возросшими возможностями средств имитационного моделирования (как технических, так и программных). Поэтому полное решение задачи определения характеристик стохастического сетевого планирования ТЦП требует привлечения имитационной сетевой модели.

 Для описания стохастической модели процесса выполнения ТЦП предлагается использовать стохастическое расширение СП [2] – стохастическо-детерминированные сети Петри (СДСП). СДСП называется такая сеть Петри, в которой каждому переходу может быть поставлена в соответствие временная переменная, являющаяся детерминированной или случайной величиной, распределенной по определенному закону, а также стохастическая переменная, влияющая на изменение структуры в соответствии со случайным выбором.

Математической моделью СДСП служит набор вида

,

где  - конечное множество позиций;

- конечное множество переходов;

 - функция предшествования множества позиций Р и переходов Т ;

 - функция следования множества позиций Р и переходов Т ;

 - функция соответствия между множеством переходов Т  и множеством детерминированных величин времени RD ;

 функция соответствия между множеством переходов Т и множеством стохастических величин времени RV, распределенных по случайному закону ;

 - функция соответствия между множеством переходов Т и множеством стохастических величин структуры RS, распределенных по случайному закону ;

 - начальная маркировка;

Для каждой операции (а, следовательно, для каждого перехода, соответствующего времени выполнения операции), кроме детерминированной RD или стохастической величины времени RV, ставится в соответствие вектор переменных  с двумя компонентами:  (вероятность выполнения i-й операции) и , значения которых принадлежат интервалу [0;1].

Динамика процесса отражается распространением меток по всем позициям сети, соответствующим условиям успешного выполнения операций, согласно правилам для детерминированных сетей со следующими особенностями.

Запуск разрешенного к срабатыванию перехода  и помещение фишки соответствующего веса в выходную позицию перехода происходит в случае выполнения условия

,                                                  (1)                                                             

где  - величина, распределенная на [0;1] по случайному закону .

В случае невыполнения неравенства (1) процесс реализации операции повторяется до  раз (где  - максимальное число повторений i-й операции, определяемое "временным окном" для проведения операции и ее вероятностными характеристиками).

В выходную позицию i-го перехода помещается фишка, вес которой определяется по формуле

,

где  - множество входных позиций i-го перехода,  - число повторений i-й операции (),  -детерминированная  либо стохастическая   величина времени срабатывания i-го перехода (соответствует времени выполнения i-й операции).

Для описания и моделирования процесса выполнения ТЦП с помощью аппарата СДСП необходимо в дополнение к обычным исходным данным для детерминированных СП, представить следующие исходные данные:

- вектор , включающий номера тех переходов, по которым необходимо получить статистическую информацию;

- вектор детерминированных времен срабатывания переходов , куда записываются временные переменные, соответствующие детерминированным величинам срабатывания переходов (детерминированные величины длительностей операций и времен ожиданий);

- вектор характеристик видов законов времен операций . Если i-я операция имеет детерминированное время выполнения, то , если же времени выполнения i-й операции соответствует стохастическая переменная, то компоненте  ставится в соответствие цифра, характеризующая определенный вид закона распределения;

- матрицу случайных параметров времен операций , в которой для различных законов распределения длительностей операций описываются параметры, необходимые для работы генератора случайных чисел и реализации заданного распределения;

- вектор вероятностей выполнения операций .

В процессе имитационного моделирования будем использовать случайные величины, имеющие следующие виды распределений: равномерное, нормальное, экспоненциальное, b-распределение. Равномерное, нормальное и               b-распределение служат для задания длительностей операций, а экспоненциальное – для формирования потока отказов.

Также в процессе стохастического моделирования процесса выполнения ТЦП необходимо учитывать вероятность выполнения отдельных операций.

Необходимое число реализаций n имитационной модели можно определить по формуле

,

где e - точность, Р – доверительная вероятность.

Однако последняя формула получена в расчете на наихудший случай, когда, например искомая вероятность непревышения времени выполнения ТЦП заданного времени . Количество необходимых опытов можно значительно уменьшить следующим образом. Вначале провести сравнительно небольшое количество опытов  (например, ). Затем оценить значения  и , определить необходимое количество опытов n и, при , провести оставшееся количество опытов. Таким образом,  процесс оценки качества плана проведения ТЦП может быть представлен в виде последовательности следующих этапов.

Этап 1.  Ввод исходных данных (порядок выполнения операций, законы распределения длительностей операций, "временные окна" и т.д.).

Этап 2. В соответствии с заданными законами распределения генерируются длительности операций. Сетевой план рассматривается как детерминированный, но с учетом вероятностей выполнения отдельных операций. Рассчитываются все необходимые характеристики.

Второй этап повторяется  раз. Затем рассчитывается необходимое количество реализаций модели, после чего, при необходимости второй этап повторяется до накопления статистического материала требуемого объема.

Этап 3. Обработка данных, расчет вероятностных характеристик всего плана в целом, выдача результатов.    

Таким образом, аппарат СДСП является эффективным средством моделирования процесса реализации ТЦП с учетом параллельно-синхронного выполнения операций со случайной длительностью. Возможность по случайным законам менять структуру модели ТЦП и время выполнения операций позволяет с достаточно высокой степенью адекватности описывать реально проводимые ТЦП. Модели, описанные с помощью СДСП, имеют возможность учета большого количества параметров, влияющих на эффективность функционирования всего производственного предприятия в целом.

Проведенный модельный эксперимент показал, что применение имитационного моделирования процесса реализации ТЦП с использованием стохастико-детерминированных временных сетей Петри позволяет получать более точные характеристики оценки качества различных планов проведения ТЦП, что позволит повысить эффективность планирования ТЦП с учетом стохастической длительности операций.

 

Литература:

1.   Филипс Д., Гарсиа-Диас А. Методы анализа сетей: Пер. с англ. – М.: Мир, 1984. – 496 с.

2.   Котов В.Е. Сети Петри.- М.: Наука, 1984. – 160 с.