Технические науки/12.Автоматизированные системы управления на производстве.

Демидов К.О., студ.; Петраков Ю.В., д.т.н., проф.;

Національний технічний університет України «Київський політехнічний інститут», Україна

Визначення швидкодії системи автоматичного регулювання розміру виробу при безцентровому шліфуванні

Зовнішні характеристики оброблюваних деталей відіграють високу роль у сучасному машинобудуванні. Все більше замовників висувають вимоги щодо надання поверхневому шару обробленої деталі високих параметрів шорсткості, для подальшого використання у різних механізмах. Зазвичай безцентрове шліфування використовую для обробки кілець підшипників. Найменший брак при їх обробці може призвести до появи вібрації і до руйнування механізму. Збереження точності при наданні високих параметрів шорсткості за найменший час є однією з основних проблем у шліфувальному процесі.

Нехай, наприклад, в результаті зношування шліфувального круга або через будь-яку іншу причину діаметр виробу, що шліфується, став перевищувати той, що вимагається. В цьому випадку напруга від перетворювача і вихідна напруга електронного підсилювача зменшуються і порушується умова рівноваги системи, тобто помилка збільшується. Двигун переміщає рухому бабку вперед, в напрямку компенсації зменшення діаметра виробу, що шліфується. Якщо діаметр деталі зменшився, то система автоматично діє у протилежний бік, стабілізуючи потрібний розмір.

Але система регулювання досить складній механізм, який має свої характеристики, комбінуючи які можна буде впливати на швидкодію системи.

При проектуванні та використанні таких систем постає проблема оптимальних параметрів системи.

Для того, що б порівнювати різні варіації параметрів раціональніше скласти прикладну програму моделювання системи автоматичного регулювання розміру виробу, що шліфується, на безцентрово-шліфувальному верстаті.

Розроблений мною програмний продукт має інтерфейс приведений на рис.1 . На осцилографі представлені графіки зміни глибини різання (1) та відповідний їй, процес реагування системи (2) з її швидкодією. З графіку 2 можна визначити швидкодію перехідного процесу, що дозволить підібрати більш оптимальні параметри системи для поліпшення точності верстату.

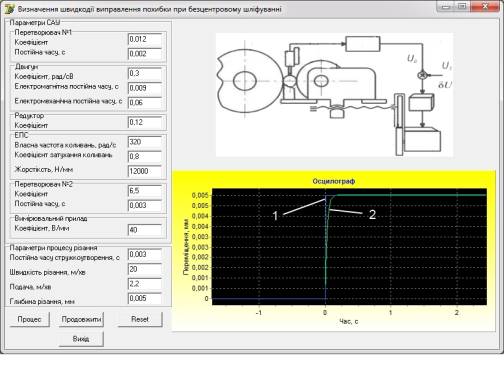
Рис.1 – Інтерфейс програмного забезпечення

При нинішніх швидкостях оброблення швидкість реагування системи на будь-які відхилення від налаштування повинні не перевищувати соті, або навіть на тисячні долі секунди. Розглядувана мною система досить складний механізм, рух якого описується рівнянням 8-го порядку. Отже постає питання, у чисельному методі інтегрування. Точність чисельного інтегрування залежить від величини кроку і часу інтегрування, який визначає кількість кроків. При зменшенні кроку точність інтегрування на кожному кроці збільшується, але збільшуватиметься і кількість кроків, що може призвести до погіршення визначення кінцевого результату. Як завжди у таких випадках оптимальним буде компромісне визначення величини кроку. Найбільш точні результати дає метод чисельного інтегрування Рунге-Кутта 4-го порядку:

Де

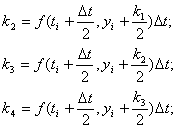
Алгоритм цієї процедури представлений на рис.2. В алгоритмі застосовані наступні позначення: delt – крок інтегрування, n – порядок системи, model – процедура обчислення правих частин математичної моделі системи.

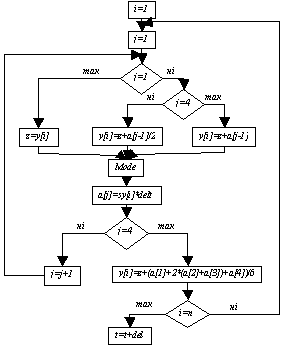
Рис.2 Алгоритм чисельного інтегрування за методом Рунге-Кутта 4-го порядку

На даному етапі розвитку машинобудування необхідність у подібних програмних засобах стоїть гостро. Проте визначення необхідних параметрів досліджуваної системи досить складний та тривалий процес. Виходом буде співробітництво з виробниками верстатів, для того, всі необхідні параметри були визначені на етапі конструювання верстату.

Дана сфера наукових досліджень нова й не вивчена досконало. Тому я пропоную звернути увагу на данні проблеми.