К.т.н., Красовский С.С.,
Хорошайло В.В.
Донбасская государственная машиностроительная академия
ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ РЕДКОУДАРНОГО ГАЙКОВЕРТА
ДЛЯ ЗАТЯЖКИ КРУПНЫХ РЕЗЬБОВЫХ СОЕДИНЕНИЙ
В современных
машинах во многих случаях резьбовые соединения являются ответственными
элементами, прочность и долговечность которых во многом определяют надежность
работы конструкции в целом.
Основные проблемы,
возникающие при сборке резьбовых соединений, с одной стороны, связанны с
необходимостью повышения производительности труда, следовательно, с высоким
уровнем механизации процесса сборки, с другой – с необходимостью обеспечения высокой
степени точности затяжки[1].
Целью работы
является теоретическое исследование применения редкоударного гайковерта [2], [3]
и влияния его энергосиловых параметров на эффективность затяжки крупных
резьбовых соединений.
Процесс
ударной затяжки резьбовых соединений во многом отличается от статической
затяжки. Его особенность заключается в практически мгновенной передаче
кинетической энергии вращающегося ударника наковальне [4]. Полученная
наковальней энергия (энергия единичного удара гайковерта) расходуется на
поворот гайки, упругую крутильную деформацию шпинделя гайковерта и на упругое
закручивание стержня болта:
![]() (1)
(1)
Величина энергии, идущая на упругое закручивание стержня болта, в
значительной степени зависит от соотношения моментов трения в резьбе и на торце
гайки [5]. Если первый из них меньше второго (МР < МТ),
то после каждого удара стержень болта остается закрученным моментом трения в
резьбе МР и удерживается от раскручивания моментом трения на торце
гайки. Потери энергии на упругое закручивание стержня болта при каждом ударе в
этом случае оказываются незначительными:
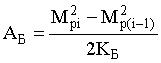 (2)
(2)
где Mpi и
Мp(i-1) – моменты трения в резьбе после i-го и (i-1)-го ударов;
КБ – крутильная жесткость стержня болта.
При обратном соотношении
моментов трения (МР > МТ) после снятия ударной
нагрузки происходит раскручивание стержня болта, и потери энергии на его
закручивание от момента трения на торце при предыдущем ударе возрастают до
момента трения в резьбе:
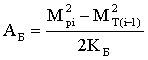 (3)
(3)
где МТ(i-1) –
момент трения на торце гайки после (i-1)-го
удара.
Рассмотрим подробнее
факторы, влияющие на соотношение этих моментов трения. При затяжке стержень
болта испытывает кручение моментом (![]() ):
):
![]() (4)
(4)
где Q – усилие
затяжки;
d – средний диаметр резьбы;
![]() угол подъема винтовой линии;
S – шаг резьбы;
угол подъема винтовой линии;
S – шаг резьбы;
![]() – угол трения;
– угол трения;
![]() ` – коэффициент трения в резьбе;
` – коэффициент трения в резьбе;
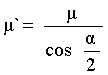 (5)
(5)
![]() – коэффициент трения
фрикционной пары;
– коэффициент трения
фрикционной пары;
![]() – угол профиля
резьбы.
– угол профиля
резьбы.
В момент остановки момент трения на торце гайки
![]() (6)
(6)
где ![]() T –
коэффициент трения на торце гайки;
T –
коэффициент трения на торце гайки;
RT – радиус трения опорной поверхности гайки:
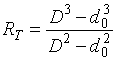 (7)
(7)
где D – наружный
диаметр кольцевого торца;
d0 – диаметр резьбы.
Анализ конструкций
крупных резьбовых соединений показывает, что величины d и RT
для всех резьб находятся в пределах:
RT=0,65
d0
Тогда, сравнивая Mp и MT,
получим условие, при котором момент на торце больше момента в резьбе:
![]() (8)
(8)
Принимая ![]() ≈ 0,1р` можно
записать для метрической резьбы:
≈ 0,1р` можно
записать для метрической резьбы:
![]()
Таким образом, стопорение стержня болта от
раскручивания будет происходит при условии, что ![]() Т ≥ 0,82
Т ≥ 0,82![]() ` или
` или ![]() T
≥ 0,95
T
≥ 0,95![]() .
.
Из этого можно сделать
вывод, что при одинаковых условиях трения в резьбе и на торце гайки (![]() Т =
Т = ![]() ), которые обеспечиваются отсутствием заедания в резьбе,
наличием смазки и так далее, стержень болта после снятия ударной нагрузки
останется закрученным моментом Mpi,
и дополнительных потерь энергии происходить не будет.
), которые обеспечиваются отсутствием заедания в резьбе,
наличием смазки и так далее, стержень болта после снятия ударной нагрузки
останется закрученным моментом Mpi,
и дополнительных потерь энергии происходить не будет.
Проведенный анализ позволяет уравнение (1) с
достаточной точностью записать в виде:
![]() (9)
(9)
Энергия, идущая на упругую крутильную деформацию
элементов гайковерта:
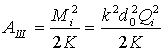 (10)
(10)
где Mi, Qi – соответственно момент затяжки и осевое усилие после
i-го удара;
КШ – крутильная жесткость шпинделя
гайковерта;
к – приведенный к диаметру резьбы коэффициент трения в резьбовом соединении, определяемый экспериментально.
Энергия, идущая на поворот гайки:
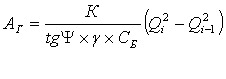 (11)
(11)
где Qi-1 – осевое усилие в крепежной детали перед i – тым ударом;
![]() – относительная
податливость крепежной детали:
– относительная
податливость крепежной детали:
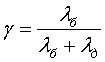 (12)
(12)
![]() б и
б и ![]() д – соответственно коэффициенты податливости болта
и промежуточных деталей.
д – соответственно коэффициенты податливости болта
и промежуточных деталей.
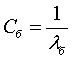 – коэффициент
жесткости болта.
– коэффициент
жесткости болта.
Таким образом, уравнение энергетического баланса
примет вид:
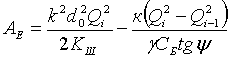 (13)
(13)
Из этого уравнения можно
получить следующие выражения для осевого усилия после i-го удара Qi, и количества ударов n необходимого
для достижения заданного усилия Q в болте:
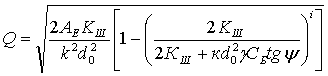 (14)
(14)
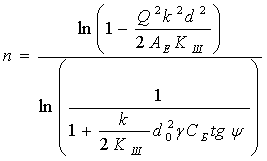 (15)
(15)
Разложив натуральные логарифмы в уравнении (13) в ряд, получим:
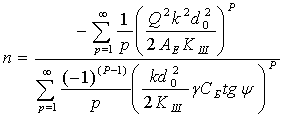 (16)
(16)
При проектировочных расчетах достаточную точность дает зависимость, в
которой учитываются только первые члены разложения в ряд логарифмических
функций:
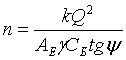 (17)
(17)
Учитывая, что:
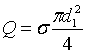 (18)
(18)
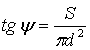 (19)
(19)
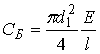 (20)
(20)
где ![]() – напряжение затяжки;
– напряжение затяжки;
S – шаг резьбы;
l – рабочая
длина болта;
E = 2![]() 107 м/мм2 – модуль упругости стали,
107 м/мм2 – модуль упругости стали,
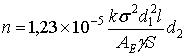 (21)
(21)
Отсюда, приняв d1≈d2≈d0,
определим энергию единичного удара гайковерта, обеспечивающую затяжку
резьбового соединения за n ударов до
напряжения:
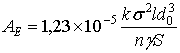 (22)
(22)
Полученная зависимость (22) позволяет определить необходимые
энергетические параметры гайковертов ударного действия для затяжки крупных
резьбовых соединений прокатных станов, задавшись предварительно напряжением затяжки
резьбового соединения, количеством ударов гайковерта и некоторыми другими
величинами. Входящая в эту зависимость относительная податливость крепежной
детали может быть определена экспериментально путем измерения деформации
крепежной детали при ее затяжке и угла поворота ![]() гайки:
гайки:
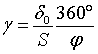 (23)
(23)
Относительная податливость крепежной детали может изменятся в диапазоне от нуля до единицы. Значения относительной податливости, близкие к нулю, будут иметь место при бесконечной податливости промежуточных деталей, т.е. при их деформации в пластической области.
При значительной
жесткости промежуточных деталей, во много раз превышающей жесткость крепежной
детали, относительная податливость приближается к единице.
Проведенные ранее исследования показали, что для различных резьбовых
соединений значения относительной податливости могут быть существенно различными.
Так, например, для шпилек горизонтальных разъемов цилиндров паровых труб их
относительная податливость находится в пределах 0,36-0,56; для стопорных и
регулирующих клапанов значение относительной податливости 0,25-0,3. В
химических сосудах высокого давления с двухконусным уплотнителем шпильки имеют
относительную податливость, равную 0,03-0,09 до выбора зазора между обтюратором
и крышкой и 0,12-0,15 после выбора этого зазора.
Крупные резьбовые соединения стягивают довольно жесткие промежуточные
детали и по своим упругим свойствам близки к резьбовым соединениям
горизонтальных разъемов. Поэтому при определении энергетических параметров
редкоударных гайковертов для затяжки резьбовых деталей крепления станин рабочих
и шестеренных клетей, крышек шестеренных клетей прокатных станов, относительная
податливость этих крепежных деталей может быть принята равной 0,5.
Приведенный к диаметру резьбы, коэффициент трения к, входящий в формулу
(22), определяется следующим выражением:
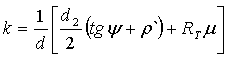 (24)
(24)
Чаще всего этот
коэффициент определяется экспериментально в процессе затяжки резьбового
соединения.
Исследованиями установлено, что для крепежных деталей металлургического
оборудования, например болтов крепления газовых затворов доменных печей, при
наличии консистентной смазки этот коэффициент равен 0,17. В предварительных расчетах его можно было принимать равным 0,2.
Учитывая то, что
существующие редкоударные гайковерты позволяют осуществлять процесс затяжки
резьбовых соединений за 4 … 15 ударов, количество n ударов гайковерта выберем равным 15. Посчитанные с учетом этого энергии единичных ударов гайковертов,
необходимые для затяжки резьбовых деталей различных диаметров до выбранных
напряжений затяжки
![]() = 80 н/м2,
представлены в таблице 1.
= 80 н/м2,
представлены в таблице 1.
Таблица 1
|
Диаметр резьбы крепежной детали d0 (мм) |
72 |
76 |
90 |
100 |
110 |
115 |
125 |
130 |
140 |
150 |
160 |
175 |
180 |
|
Расчетная энергия единичного удара гайковерта АЕ
(Дж) |
141 |
175 |
343 |
524 |
768 |
917 |
128 |
1498 |
2016 |
2656 |
3439 |
4922 |
5509 |
Выводы:
В работе выполнены теоретические и экспериментальные исследования,
определяющие влияние различных параметров редкоударных гайковертов на результат
затяжки. Рассмотрены расчетные модели и составлены основные уравнения,
позволяющие получить решение контактных задач с учетом различных граничных
условий, как для одномерной стержневой модели, так и двухмерной. Полученные результаты могут быть использованы при разработке,
проектировании и сборке, как прокатных станов, так и любого другого
оборудования.
Литература:
1.
Иосилевич, Г. Б.
Затяжка и стопорение резьбовых соединений / Иосилевич Г. Б., Строганов
Г. Б., Шарковский Ю. В. – М. : Машиностроение, 1985. – 224 с.
2.
Красовский С. С.
Анализ методов механизации сборки крупных резьбовых соединений
металлургического оборудования / С. С. Красовский,
В. В. Хорошайло, С. А. Бабенко // Восточно-Европейский
журнал передовых технологий. 6/7 (54) 2011. С. 14-16.
3.
Красовский С. С.
Классификация конструкций ударно-импульсных механизмов // Вестник ДГМА.
№ 4 (25) 2011. С. 251-256.
4.
А. с. 1710327
(СССР). Гайковерт для сборки крупных резьбовых соединений/ Красовский С. С. –
Опубл. 1992; Бюл. № 5.
5.
Красовский С. С.
Механизация сборки резьбовых соединений в машиностроении: теория, исследования,
технология, конструкции: монография / Красовский С. С. –
Краматорск: ДГМА, 2011. – 148 с. ISBN 978-966-379-515-7.