К.т.н Косюк В. И
ООО УРСП «Электрон-Звезда»,Украина
СПОСОБ
ИЗМЕРЕНИЯ ВНУТРЕННЕГО СОПРОТИВЛЕНИЯ
ХИМИЧЕСКИХ ИСТОЧНИКОВ ТОКА (ХИТ)
Внутреннее
сопротивления химического источника тока (ХИТ) является одной из важных его
характеристик. Величина этого сопротивления определяет такие параметры источника,
как максимальный ток нагрузки, тепловые потери, емкость и т.п.
Проблеме
установления зависимости между емкостью ХИТ и его внутренним сопротивлением
посвящено много работ [1-5]. В работе [1], зависимость емкости ХИТ
и его внутреннего сопротивления
описывается эмпирическим уравнением:
![]() , (1)
, (1)
где ![]() — омическое сопротивление ХИТ;
— омическое сопротивление ХИТ;
![]() — остаточная емкость ХИТ.
— остаточная емкость ХИТ.
С другой
стороны, величина внутреннего сопротивления ХИТ, которая дается в каталогах
зарубежных производителей, оценивается путем измерений на переменном токе частотой
1000 ±100 Гц в течение 1…5с. При этом
величина внутреннего сопротивления ХИТ вычисляется по формуле [1]:
![]() , (2)
, (2)
где ![]() — переменный ток через ХИТ;
— переменный ток через ХИТ;
![]() — переменное напряжение на ХИТ,
являющееся откликом на пропускаемый ток.
— переменное напряжение на ХИТ,
являющееся откликом на пропускаемый ток.
Проведение
измерений внутреннего сопротивления по приведенной выше методике предполагает
включение еще и поляризационного сопротивления помимо ![]() . Величина этого поляризационного
сопротивления заметно больше, чем
. Величина этого поляризационного
сопротивления заметно больше, чем ![]() . А поскольку ток к моменту времени t1 может и не
достигать своего стационарного состояния, измеренная величина не всегда
характеризует полное внутреннее сопротивление источника тока. Таким образом, получается полная
неопределенность в определении сопротивления ХИТ.
. А поскольку ток к моменту времени t1 может и не
достигать своего стационарного состояния, измеренная величина не всегда
характеризует полное внутреннее сопротивление источника тока. Таким образом, получается полная
неопределенность в определении сопротивления ХИТ.
В работе [2] описан другой способ определения внутреннего сопротивления
аккумуляторной батареи (АКБ), по которому измеряют ЭДС и напряжение на АКБ при
отсутствии тока и фиксированной величине переменного тока со скважностью,
равной двум. Этот ток формируется за
счет наложения на постоянный разрядный ток батареи униполярных прямоугольных
импульсов зарядного тока. При этом по полученным данным сопротивление ![]() вычисляется по следующей формуле:
вычисляется по следующей формуле:
![]() , (4)
, (4)
где ![]() — ЭДС АКБ;
— ЭДС АКБ;
![]() — напряжение на АКБ при разряде;
— напряжение на АКБ при разряде;
![]() — коэффициент формы переменного импульсного тока батареи;
— коэффициент формы переменного импульсного тока батареи;
![]() — индуктивность батареи при частоте переменного тока
— индуктивность батареи при частоте переменного тока ![]() кГц.
кГц.
Ток ![]() определяется следующей формулой:
определяется следующей формулой:
![]() , (5)
, (5)
где ![]() — расчетный ток нагрузки батареи.
— расчетный ток нагрузки батареи.
Описанный
способ обладает рядом существенных недостатков. Во-первых, при таком подходе требуются большие энергетические
затраты, т.к. для получения малой погрешности измерения емкости АКБ, её
необходимо нагружать на очень малое нагрузочное сопротивление (для получения
существенной разницы между ЭДС и напряжением при нагрузке ![]() ),
что является нежелательным. Во-вторых,
нагрузочное сопротивление нужно включать на очень малое время, т.к. иначе
произойдет разряд АКБ и возможен выход из строя нагрузочного сопротивления из-за его перегрева. В-третьих, согласно формулам (3 и 4), для
расчета
),
что является нежелательным. Во-вторых,
нагрузочное сопротивление нужно включать на очень малое время, т.к. иначе
произойдет разряд АКБ и возможен выход из строя нагрузочного сопротивления из-за его перегрева. В-третьих, согласно формулам (3 и 4), для
расчета ![]() необходимо знать значение индуктивности
необходимо знать значение индуктивности ![]() АКБ, что требует проведения дополнительных
измерений. И, наконец, внутреннее
сопротивление АКБ имеет сложный характер и включает в себя непосредственно
внутреннее сопротивление АКБ
АКБ, что требует проведения дополнительных
измерений. И, наконец, внутреннее
сопротивление АКБ имеет сложный характер и включает в себя непосредственно
внутреннее сопротивление АКБ ![]() и поляризационное сопротивление
и поляризационное сопротивление ![]() ,
которые проявляются при различных токах заряда или разряда [3, 4], а описанный
способ позволяет определить только
,
которые проявляются при различных токах заряда или разряда [3, 4], а описанный
способ позволяет определить только ![]() ,
т.е. является функционально ограниченным.
,
т.е. является функционально ограниченным.
В работе [5]
описан способ измерения сопротивления короткого замыкания ХИТ путем разряда измеряемого источника тока на
конденсаторную нагрузку. При этом
фиксируют изменение напряжения на конденсаторе (UC) и строят кривую зависимости этого напряжения
от времени и, далее, выбирая на кривой любую точку до значения напряжения
равного ![]() ,
по координатам этой точки вычисляют сопротивление КЗ. Однако по описанному способу можно определить только
,
по координатам этой точки вычисляют сопротивление КЗ. Однако по описанному способу можно определить только ![]() ,
т.е. данный способ также является функционально ограниченным и довольно
трудоемким и долговременным, несмотря на то, что максимальное время процесса
заряда конденсатора составляет доли секунды.
,
т.е. данный способ также является функционально ограниченным и довольно
трудоемким и долговременным, несмотря на то, что максимальное время процесса
заряда конденсатора составляет доли секунды.
Как
известно [3, 4], сопротивление поляризации ![]() при увеличении тока уменьшается. При больших зарядных или разрядных токах
внутреннее сопротивление ХИТ будет стремиться к постоянной величине, численно
равной омическому сопротивлению
при увеличении тока уменьшается. При больших зарядных или разрядных токах
внутреннее сопротивление ХИТ будет стремиться к постоянной величине, численно
равной омическому сопротивлению![]() ХИТ. Если к ХИТ подсоединить конденсатор, то ток в цепи конденсатора будет
изменяться от максимального до нуля и, соответственно, внутреннее сопротивление
ХИТ будет изменяться от
ХИТ. Если к ХИТ подсоединить конденсатор, то ток в цепи конденсатора будет
изменяться от максимального до нуля и, соответственно, внутреннее сопротивление
ХИТ будет изменяться от ![]() до
до ![]() .
При этом кривая заряда конденсатора
от ХИТ будет представлять собой сумму двух экспоненциальных зависимостей [6].
Первая зарядная характеристика (быстрая), обусловленная большим начальным током
заряда конденсатора, будет характеризоваться постоянной времени
.
При этом кривая заряда конденсатора
от ХИТ будет представлять собой сумму двух экспоненциальных зависимостей [6].
Первая зарядная характеристика (быстрая), обусловленная большим начальным током
заряда конденсатора, будет характеризоваться постоянной времени ![]() равной:
равной:
![]() , (6)
, (6)
где ![]() — емкость заряжаемого конденсатора.
— емкость заряжаемого конденсатора.
Напряжение на конденсаторе будет меняться согласно
следующему уравнению [7]:
![]() ,
(7)
,
(7)
где ![]() изменяется от 0 до
изменяется от 0 до ![]() ,
,
![]() — напряжение на ХИТ.
— напряжение на ХИТ.
Вторая зарядная характеристика (медленная) будет
характеризоваться постоянной времени ![]() равной:
равной:
![]() (8)
(8)
и напряжение на конденсаторе будет меняться согласно
следующему уравнению [7]:
![]() , (9)
, (9)
где ![]() изменяется от
изменяется от ![]() до
до ![]() .
.
Тогда, по следующей формуле,
![]() , (10)
, (10)
где ![]() — количество постоянных времени
— количество постоянных времени ![]() ,
соответствующих моменту времени
,
соответствующих моменту времени ![]()
можно
определить значение ![]() :
:
![]() . (11)
. (11)
На рис.1
показана структурная схема для измерения сопротивления ХИТ. На рис.2 представлены
составляющие зарядной характеристики конденсатора, а на рис. 3 - суммарная зарядная характеристика конденсатора от
измеряемого ХИТ. На рис. 4 представлена
осциллограмма реальной характеристики заряда конденсатора от стартерного
свинцового аккумулятора с номинальной емкостью ![]() ,
а на рис. 5 та же самая осциллограмма с растянутым начальным участком.
,
а на рис. 5 та же самая осциллограмма с растянутым начальным участком.
При
достижении уровня заряда конденсатора, примерно до величины ![]() начинает включаться поляризационное
сопротивление
начинает включаться поляризационное
сопротивление ![]() и ток заряда значительно уменьшается.
Анализируя кривые, приведенные на рис. 3 и рис. 4, можно утверждать, что при
уровне заряда конденсатора, равном
и ток заряда значительно уменьшается.
Анализируя кривые, приведенные на рис. 3 и рис. 4, можно утверждать, что при
уровне заряда конденсатора, равном ![]() ,
поляризационное сопротивление полностью включено. Исходя из этого, составляем
следующую систему уравнений для принятых значений уровня заряда конденсатора:
,
поляризационное сопротивление полностью включено. Исходя из этого, составляем
следующую систему уравнений для принятых значений уровня заряда конденсатора:
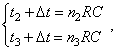 (12)
(12)
где
![]() . (13)
. (13)
Решение системы уравнений (11) относительно R дает
следующее значение:
![]() . (14)
. (14)
Исходя из (12) однозначно определяем ![]() .
.
Значения уровня заряда конденсатора от измеряемого ХИТ
в зависимости от ![]() определяются следующей формулой [7]:
определяются следующей формулой [7]:
![]() , (15)
, (15)
где ![]() ,
,
![]() — время заряда конденсатора до заданного уровня,
— время заряда конденсатора до заданного уровня,
![]() — постоянная времени заряда конденсатора.
— постоянная времени заряда конденсатора.
Значения n
для некоторых значений U представлены в таблице 1.
Таблица 1.
|
U |
0,22 |
0,3 |
0,39 |
0.5 |
0,63 |
0,7 |
0,78 |
0,8 |
0,87 |
0,9 |
0,92 |
0,95 |
0,96 |
|
n |
0,25 |
0,37 |
0,5 |
0,7 |
1 |
1,2 |
1,5 |
1,6 |
2 |
2,3 |
2,5 |
3 |
3,2 |
Так, если выбрать время заряда конденсатора,
соответствующее значениям ![]() ,
равным 0,39; 0,9 и 0,95, что достигается при следующих значениях
,
равным 0,39; 0,9 и 0,95, что достигается при следующих значениях ![]() :
:
![]() ;
;
![]() и
и ![]() ,
то выражения (5) и (8) можно записать в следующем виде:
,
то выражения (5) и (8) можно записать в следующем виде:
![]() , (16)
, (16)
![]() . (17)
. (17)
Таким
образом, измерив время заряда конденсатора известной емкости от измеряемого ХИТ
в трех точках, заданных по уровню заряжаемого напряжения, можно вычислить значения
внутреннего сопротивление ХИТ ![]() ,
сумму этих сопротивлений
,
сумму этих сопротивлений ![]() и поляризационное сопротивление
и поляризационное сопротивление ![]() .
Такой способ измерения внутреннего сопротивления ХИТ представляется более
полным и имеет ряд преимуществ перед способами перечисленными выше:
.
Такой способ измерения внутреннего сопротивления ХИТ представляется более
полным и имеет ряд преимуществ перед способами перечисленными выше:
1)
исключается
неопределенность при измерении сопротивлений ХИТ;
2)
исключается
опасность полного разряда измеряемого ХИТ;
3)
отсутствие
больших энергозатрат делают этот способ
измерения сопротивления ХИТ более экономичным;
4)
способ
позволяет измерить обе составляющие ![]() и
и ![]() внутреннего сопротивления ХИТ, что особенно
важно при эксплуатации ХИТ с переменными токами нагрузки;
внутреннего сопротивления ХИТ, что особенно
важно при эксплуатации ХИТ с переменными токами нагрузки;
5)
упрощается
процесс измерения и расчета составляющих полного сопротивления измеряемого ХИТ.
На рис. 6 и рис. 7 представлены осциллограммы реальной
характеристики заряда конденсатора от щелочного элемента типа ![]() .
На рис. 8 и рис. 9 представлены осциллограммы реальной характеристики заряда
конденсатора от литиевого элемента. Как видно из осциллограмм приведенных на
рис. 6-9 поляризационное сопротивление
.
На рис. 8 и рис. 9 представлены осциллограммы реальной характеристики заряда
конденсатора от литиевого элемента. Как видно из осциллограмм приведенных на
рис. 6-9 поляризационное сопротивление ![]() для этих типов ХИТ начинает включаться при
уровнях заряда конденсатора меньших
для этих типов ХИТ начинает включаться при
уровнях заряда конденсатора меньших ![]() .
.
ЛИТЕРАТУРА
1. Таганова
А. А., Бубнов Ю. И., Орлов С. Б.
Герметичные химические источники тока: элементы и аккумуляторы,
оборудование для испытаний и эксплуатации. Санкт-Петербург. : Химиздат, 2005.
264 с.
2. А.С. СССР
№ 1742908 А1, H01M 10/48, БИ № 23, 1992
г. Способ определения внутреннего сопротивления аккумуляторной батареи.
3. Романов
В. В., Хашев Ю. М. Химические источники тока. М.: Советское радио, 1978. 264 с.
4. Вайлов А.
М., Эйгель Ф. И. Автоматизация контроля
и обслуживания аккумуляторных батарей. М. : Связь, 1975. 87 с.
5. А.С. СССР
№ 547878, H01M 10/48, БИ № 7, 1977.Способ измерения сопротивления короткого
замыкания химического источника тока.
6. Патент
России № 2328012, G01R 31/36, БИ № 18, 2008. Способ измерения сопротивления
химических источников тока.
7. Зельдович
Я. Б., Яглом И. М. Высшая математика
для начинающих физиков и техников. М. : Наука, 1982. 510 с.
4
![]()
![]()
![]()
![]()
![]()
![]()
2
![]()
![]() +
+
![]()
![]()
![]()
![]()
1 3
![]()
![]()
1- измеряемый ХИТ; 2- безинерционный ключ на замыкание
цепи с малым переходным сопротивлением; 3- конденсатор, заряжаемый от
измеряемого ХИТ; 4- запоминающий осциллограф.
Рис. 1
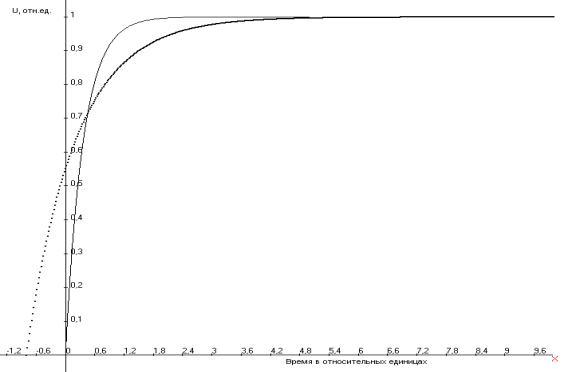
Рис.2
Составляющие зарядной характеристики конденсатора от
химического источника тока
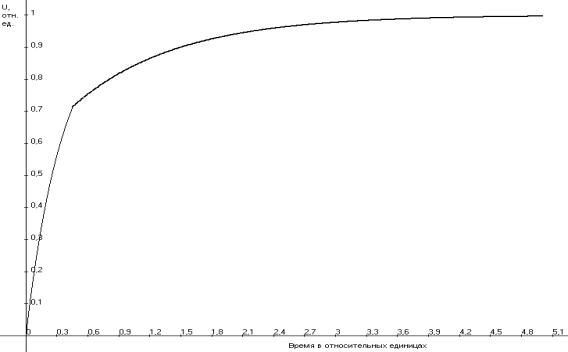
Рис.3
Суммарная зарядная характеристика конденсатора от
химического источника тока
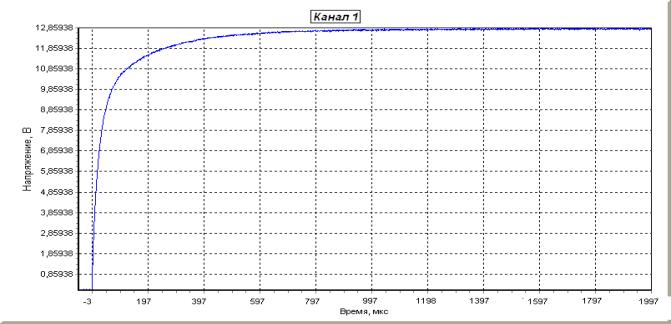
Рис.4
Осциллограмма характеристики заряда конденсатора от
стартерного
свинцового
аккумулятора
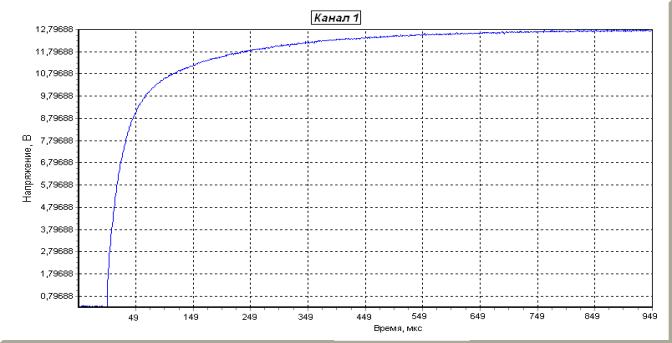
Рис.5
Осциллограмма
характеристики заряда конденсатора от стартерного
свинцового
аккумулятора с растянутым начальным участком.
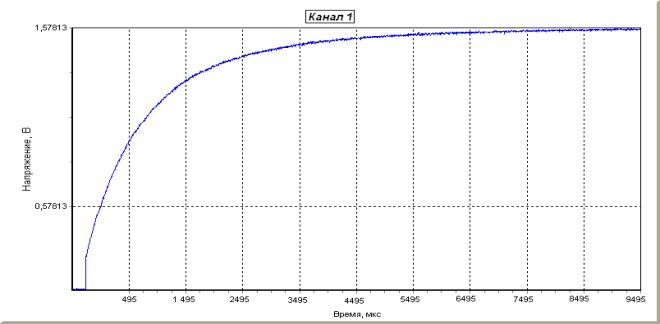
Рис.6
Осциллограмма характеристики заряда конденсатора от
щелочного элемента типа ![]()
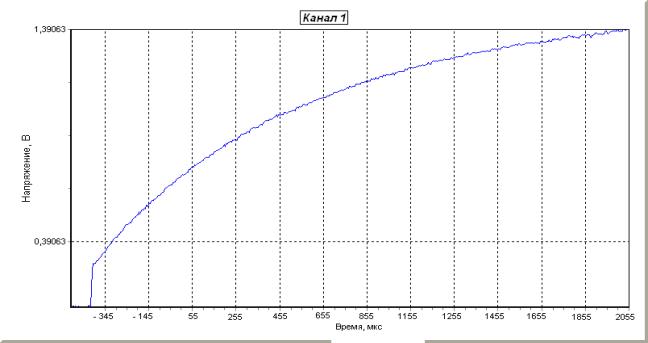
Рис.7
Осциллограмма
характеристики заряда конденсатора от щелочного
элемента типа ![]()
с растянутым начальным участком.
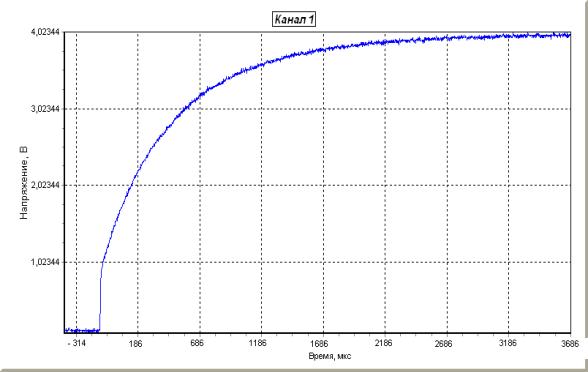
Рис.8
Осциллограмма
характеристики заряда конденсатора от литиевого элемента.
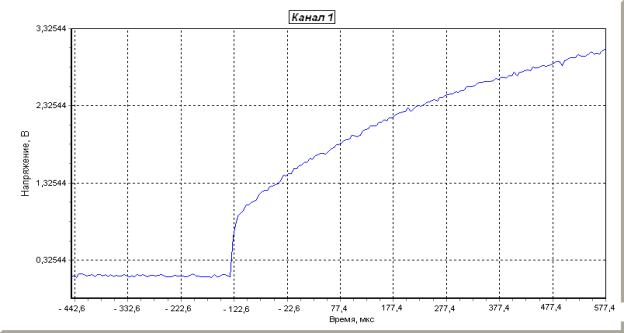
Рис.9
Осциллограмма характеристики заряда конденсатора от
литиевого
элемента с растянутым начальным
участком.