Технічні науки / 6. Электротехніка і радіоелектроніка

К.т.н. Сідєлєв М.І.

Чорноморський державний університет, Україна

Топологічно-ізоморфний підхід у комп’ютерному моделюванні електромагнітних кіл

Комп’ютерне моделювання електротехнічних та електронних пристроїв і на сьогодні відіграє особливу роль у проектуванні економічних та у технічному плані ефективних приборів різного призначення. Воно дозволяє не лише прискорити розрахункові роботи і поліпшити якість проектування, але і створює сприятливі умови для розвитку теорії моделювання енергомістких частин перетворювачів електроенергії.

При розрахунку енергоємності модельованого пристрою дуже важливо вибрати метод, що дозволяє точно оцінити накопичування та втрати енергії в елементах схеми. Це може вплинути на кінцевий результат дослідження, наприклад коефіцієнт корисної дії (ККД), коефіцієнт потужності тощо.

При дослідженні пристроїв з використанням ЕОМ істотну роль відіграють принципи подання структури і методи опису електромагнітних кіл (ЕМК). Принципи топологічно-изоморфного моделювання (ТІМ) добре вивчені і успішно використовуються в автоматизації проектування ЕМК. Однак сучасні електронні пристрої з електромагнітними компонентами у своєму складі зазвичай мають велику кількість ємнісних елементів, що потребує подальшого розвитку методів ТІМ і способів описання ЕМК. Одним із шляхів вирішення цієї проблеми є поділ ЕМК на підсхеми.

Оптимальне проектування ЕМП вимагає розробок методів з використанням цифрових обчислювальних машин. Як правило, такі методи базуються на класичній теорії ЕМК, підкріпленої сучасними науковими роботами інститутів, проектно-конструкторських підприємств та їх багаторічним досвідом моделювання. Сучасні математичні методи і технічна база (ЕОМ) дозволили якісно розширити можливості дослідження електромагнітних перетворювачів.

Вибираючи відповідний опис для дослідження фізичних процесів, слід враховувати мету, напрямок розробок, ступінь деталізації вузлів пристроїв, що моделюються. Однією з найважливіших проблем автоматизації наукових досліджень (АНД) ЕМП є дослідження енергетичних процесів і характеристик (ККД, коефіцієнт потужності тощо). При цьому слід враховувати втрати енергії на кожному елементі схеми. Ряд пристроїв (електромагнітні перетворювачі, накопичувачі енергії електричного та магнітного поля, блоки живлення електронної апаратури...) включають в себе потужні магнітні системи, де мають місце в достатній мірі, щоб їх враховувати, втрати на магнітний гістерезис і вихрові струми. Щоб локалізувати втрати в сталі, необхідно магнітне коло представляти так само докладно, як і електричну.

У даний час розроблені методи представлення ЕМК, де використовується поділ схеми на електричні та магнітні кола. Для представлення графа магнітного кола використовують матрицю iнциденцiй або частіше контурну матрицю магнітних зв'язків. Зв'язок між магнітним і електричним графом забезпечується матрицею виткових зачеплень , котра залежить від числа витків, що сидять на магнітних стрежнях, і способу з'єднань. Існує два способи формування . В одному випадку реалізується зв'язок електричної гілки з контуром магнітного потоку, в іншому - зв'язок контурного потоку з електричною гілкою. Вибір матриці визначається конкретною реалізацією математичних моделей ЕМК.

Опис електричних кіл широко використовується в промисловій електроніці із застосуванням топологічних методів. Структура електричних кіл описується матрицями iнциденцiй, контурних струмів, перетинів і т.д., що дозволяє широко використовувати теорію матриць при складанні описів ЕМК. У свою чергу теорія матриць дозволяє вирішувати проблеми моделювання електричних кіл частинами.

Якщо у схемах присутні всі відомі типи елементів (резистори, конденсатори, індуктивності тощо), то матриці, що зберігають структуру електричного кола погано узгоджуються з математичним описом. У таких випадках електричне коло розбивають на підсхеми, в котрих локалізуються елементи одного типу. Наприклад, можна виділити лінійну резистивну частину схеми, а нелінійні елементи і компоненти, що накопичують енергію, замінити джерелами струму і електрорушійних сил. Таким чином, дизайнер повинен займатися перетворенням вихідної і складанням нової (еквівалентної) схеми.

У цій роботі приділено особливу увагу простоті подання вихідної інформації, що виключає еквівалентні перетворення електричного кола.

Нехай електричні кола, для котрих розробляється математична модель, представлені з двополюсними компонентами. Тоді, залежно від характеру компонентів, гілки графа електричних схем розділяємо на наступні типи:

1) гілки пасивних двополюсників (ємностей);

2) гілки залежних і незалежних джерел напруги з лінійними і нелінійними активними опорами.

Розглядаючи гілки за типами, граф електричної схеми можна умовно розділити на підграфи "ємнісний" та "резистивний". Надалі поняття "підграф" замінимо на "граф", коли будемо розглядати їх як відокремлені структури. Якщо пронумерувати спочатку гілки й вузли заходів дуг дерева ємнісного графа, а потім гілки й вузли резистивного графа, тоді матриця інциденцій , котра відображає структуру електричного кола, автоматично розбивається на блоки:

.

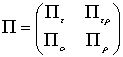Матриці і містять відповідно вузли входів і виходів дуг дерева ємнісного графа. Вузли резистивного підграфа, що потрапили в , складають матрицю , а інша частина вершин - матрицю .

Таким чином, "ємнісний" граф описується топологічною підматрицею . Базові вузли його винесені в окремий блок . Цей блок забезпечує зв'язок між базовими вузлами "ємнісного" графа і "резистивним" графом, котрий представлений підматрицею . Інші вузли ємнісного графа можуть бути і найчастіше пов'язані з "резистивним" графом, і цей зв'язок описаний підматрицею .

Магнітне коло представляється так само докладно, як і електричне і описується контурною матрицею . При формуванні графа кожне магнітне зв'язане коло може доповнюватися "повітряною" гілкою, параметри котрої повинні бути підібрані так, щоб у можливій мірі описувати потоки розсіювання.

Розглянемо магнітну гілку (рис.1). На стержень з магнітного матеріалу довжиною і перетином , в загальному випадку має зазор , намотані одна або кілька обмоток з кількістю витків . Магнітний опір гілки обчислюється за формулою

,

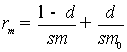де - магнітна проникність стержня, - магнітна проникність зазору. Перетин зазору і стрежня передбачаються однаковими за умови, що .

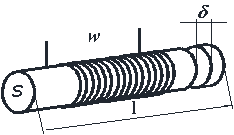
Рис.1. Конструктивні параметри магнітної гілки

Індуктивність гілки може бути визначена виразом: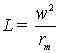

Зв'язок магнітного графа з електричним забезпечується матрицею виткових зачеплень . Її розмірність за рядками відповідає контурній матриці , а по стовпцях - матриці провідності . Елементи матриці заповнюються наступному чином. Якщо початок і кінець електричної обмотки збігається з обраним напрямом магнітного потоку, то у відповідну клітку вписується число витків зі знаком "плюс", якщо напрями не збігаються, то число витків - зі знаком "мінус".

Використовуючи блочну структуру матриці , визначимо розподілення струмів у схемі наступним чином:

, (1)

де - відповідно вектори струмів, електрорушійних сил та магнітних потоків.

Виразом (1) реалізований метод вузлових потенціалів із застосуванням окремих блоків матриці

Таке використання блочних матриць при складанні математичного опису електричних кіл названо конструктивно-топологічним підходом.

Зв'язок між магнітним потоком і струмом електричного кола визначається за методом контурних струмів для магнітного кола:

, (2)

де - діагональна матриця магнітних опорів.

Похідна напруги на ємності визначається її струмом заряду:

(3)

Проведемо розтин, що охоплює обидва вузла, до котрого підключена ємність. Тоді сума струмів, що протікають в розрізаних гілках згідно з першим законом Кіргофа, буде дорівнює нулю. Використовуючи топологічну матрицю П цей закон реалізуємо наступним чином:

. (4)

Вищенаведені співвідношення пов'язують всі основні змінні, котрі визначають стан електричного і магнітного кола. Таким чином, матричні рівняння (1)-(4) становлять повну систему диференціальних рівнянь електромагнітного кола.

Математичний опис (1)-(4) передбачає використання резисторів, ємностей, індуктивних елементів і джерел ЕРС. Проте в перетворювальних пристроях є елементи з нелінійними характеристиками - керовані і некеровані напівпровідникові діоди, сердечники з магнітного матеріалу. Для моделювання перетворювальних пристроїв з цими елементами, не виходячи за рамки описання (1)-(4), потребує використання спеціальних математичних моделей.

Висновки

Отримано математичний опис електромагнітних пристроїв, в котрому індуктивні параметри визначаються геометричними розмірами і характеристиками магнітопроводів.

Топологія електричного ланцюга представлена матричними блоками , що дозволило "зконструювати" математичний опис, котрий враховує одночасно розподіл струмів і зарядів в елементах схеми.