Технические науки/8. Обработка материалов в
машиностроении
К.т.н.
Фролов В.К., к.т.н. Гладський М.М., Антонченко В.О.
Національний
технічний університет України «КПІ»
Математичне
моделювання процесу внутрішнього шліфування
В наш час інженерам
доволі часто доводиться зустрічатися з задачами, що не піддаються аналітичному
рішенню або вимагають величезних витрат на експериментальну реалізацію. Тому
все частіше єдиною можливістю отримання швидкого результату є комп’ютерне
математичне моделювання. При цьому широко використовується метод кінцевих
елементів.
Однією з провідних
програм для кінцевоелементного аналізу є ANSYS, яка відрізняється великою
кількістю вирішуваних задач та відносною простотою в освоєнні і використанні. Серед
можливостей моделювання в програмі ANSYS є моделювання нестаціонарних теплових
задач.
При аналізі процесу
пружного внутрішнього шліфування нас цікавлять температура на поверхні деталі
та термічні деформації, що виникають на першій хвилині оброблення і можуть
вплинути на точність результатів вимірювань, тому в якості вихідних даних прийнято:
·
тепловий потік,
що діє на ділянку деталі;
·
розміри поверхні
деталі, що контактує з шліфувальним кругом;
·
швидкість
обертання деталі;
·
початкова
температура деталі;
·
температура
навколишнього середовища;
·
коефіцієнт
теплообміну між деталлю та середовищем;
·
фізичні
властивості матеріалу деталі.
Для моделювання
взято деталь у формі кільця з наступними розмірами:
внутрішній діаметр 100 мм; товщина
стінки 10 мм; довжина 50 мм. Матеріал
деталі – сталь Х12ВМ.
Для побудови моделі використовувався
метод «знизу догори», який передбачає послідовне створення точок, ліній, площин
і об’ємів.
Виходячи з того, що
процес є нестаціонарним, тобто температурні поля залежать від часу оброблення,
рішення буде покроковим.
Кількість кроків для
обчислення одного обороту деталі приймемо як відношення довжини кола
оброблюваної поверхні до довжини дуги контакту заготовки з кругом:
![]() ·
·
В результаті
отримаємо модель деталі (рис.1,а), а після розбивки – кінцевоелементну
модель (рис.1,б).
|
а) |
б) |
|
Рис.1. Об’ємна модель оброблюваної деталі (а) та модель, яку розбито на кінцеві елементи (б) |
|
Для більш докладного уявлення теплових процесів при шліфуванні зробимо
тепловий аналіз для декількох обертів При моделюванні
визначалась температура на поверхні деталі після одного, п’яти, двадцяти,
сорока та п’ятдесяти її обертів і порівнювалась з критичною, що дорівнює 1088˚К. На рис.2,а показано
розподіл температурних полів після одного оберту деталі, на рис.2,б – після
п’ятдесяти.
Порівняємо температури на поверхні деталі для одного, п’яти, двадцяти,
сорока та п’ятдесяти обертів (рис.3, рис.4).
Для порівняння виберемо момент, коли процес шліфування закінчується,
тобто в кінці кожного досліджуваного оберту деталі.
Дані про температуру зчитувались з поверхні деталі в площині, що
проходить паралельно торцю деталі через точку з максимальною температурою.
|
а) |
б) |
|
Рис.2.
Температурні поля на поверхні оброблюваної деталі після одного (а) та
п’ятдесяти (б) її обертів |
|
Аналіз даних дозволяє говорити про накопичення тепла і дає уявлення про
характер розподілу температур по поверхні деталі.
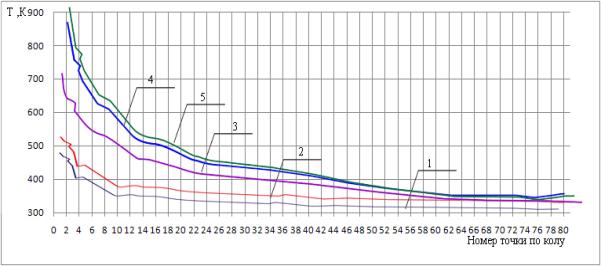
Рис.3.
Порівняння температур на поверхні деталі
(1
– після одного оберту; 2 – після п’яти обертів, 3 – після двадцяти обертів; 4 – після сорока обертів, 5 – після п'ятдесяти
обертів)
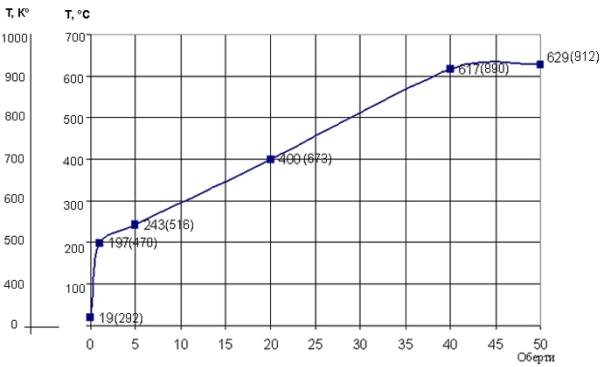
Рис.4.
Залежність температури в зоні шліфування від кількості обертів
Максимальна температура на поверхні після
одного, п’яти, двадцяти, сорока та п’ятдесяти її обертів складає відповідно 470˚К, 516˚К, 673˚К,
890˚К, 912˚К і не перевищує температурний поріг. З отриманих даних
видно, що процес поступово стабілізується, і критична температура не буде
досягнута при подальшому шліфуванні. Тобто при цьому режимі оброблення припалів
на поверхні не буде.



