Технические науки/8. Обработка материалов в машиностроении

К.т.н. Гладський М.М., к.т.н. Фролов В.К., Антонченко В.О.

Національний технічний університет України «КПІ»

Визначення пружних деформацій довгих оправок конічної форми

Існує ряд технологічних елементів, під час виготовлення яких є необхідність врахування пружних деформацій, що спричиняють вимірювальні прилади при контролюванні розмірів оброблювальних поверхонь. Прикладом таких елементів є довгі тонкі оправки, що у подальшому, наприклад, використовуються для виготовлення безшовних труб. Такі оправки мають конічну форму, що обмежує застосування довідникових рівнянь опору матеріалів.

Метою даної роботи є розроблення практичного методу для корегування сигналів вимірювальних приладів на станках з ЧПУ, що зумовлено прогином консольно-закріплених конусних оправок під дією сервісних сил приладів на пружинній основі.

На рис.1 представлено розрахункову схему навантаження консольно-закріпленої конічної балки.

Рис.1. Розрахункова схема балки конічної форми

Припускається, що у місці закріплення балки не виникають переміщення та кут повороту поперечного перетину дорівнює нулю.

Зрозуміло, що ліва частина, яку зображено пунктиром на рис.1, не буде чинити опір і не впливатиме на прогин у точці прикладання сили і тому необхідно розглядати лише праву частину досліджуваної системи.

Нехай задано конусність досліджуваної балки , де – це довжина конусу та – діаметр поперечного перерізу в місці закріплення конусу. Розглянемо довільний поперечний переріз на відстані , як зображено на рис.1. Тоді діаметр у досліджуваному перерізі можна виразити у вигляді .

Прогин у точці прикладання сили можна визначити за допомогою диференційного рівняння зігнутої осі балки у наступному вигляді:

, (1)

де , згинаючий момент та момент інерції відповідно. Приймається, що оправку виготовлено з одного матеріалу з постійним модулем пружності . Знаходимо згинаючий момент та момент інерції:

;

,

де – точка прикладання сили .

Перепишемо рівняння (1):

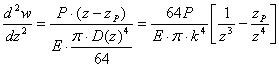. (2)

Проінтегрувавши двічі рівняння (2), отримаємо

.

Константи інтегрування знаходимо із граничних умов закріплення балки:

, .

Тоді рівняння зігнутої осі балки приймає наступний вигляд:

.

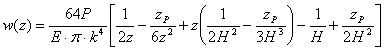Приймаючи остаточно отримаємо

. (3)

Отримане рівняння дає змогу визначити прогин консольно-закріпленої оправки конусної форми у довільній точці прикладання сили та скорегувати показники вимірювального обладнання під час контролю розмірів оброблюваної поверхні.

Треба зазначити, що в деяких інженерних рішеннях знаходять наближене значення прогину балок конічної форми шляхом визначення переміщень еквівалентної циліндричної балки за середнім діаметром конусу. Однак це супроводжується виникненням певної похибки. Для точного вирішення задачі необхідно визначити еквівалентний діаметр циліндру, що чинитиме однаковий опір у порівнянні із конічною балкою.

Визначимо переміщення в точці прикладання сили циліндричної балки. Застосувавши вищеописаний алгоритм, остаточно отримаємо:

, (4)

де – діаметр циліндру.

Порівнявши рівняння (3) та (4), знайдемо діаметр еквівалентного циліндру за умови :

. (5)

На рис. 2 показано порівняльний аналіз визначення прогину конічної балки за середнім діаметром конусу та за запропоновую методикою. Як видно з рисунку, при похибка сягає 70%. Рівняння (5) дає змогу використовувати довідкові рівняння опору матеріалів для визначення прогину довільної балки конічної форми.

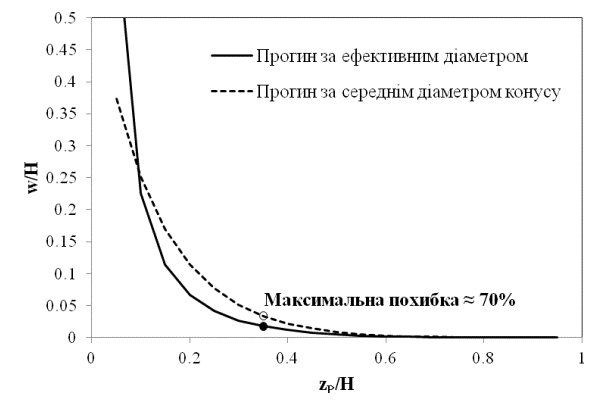
Рис.2. Порівняльний аналіз визначення прогину конічної балки