Экономические
науки/ 8.Математические методы в экономике.
Д.ф.-м.н. Андриенко В.А.,
Магистр факультета
математики Науменко К. В.
Одесский национальный
университет им. И. И. Мечникова, Украина
Оценка
вероятности банкротства страховой компании в классической модели риска
Классический
процесс риска, описывающий эволюцию во времени капитала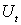 
страховой компании,
задается соотношением
,
где
t – время; u – начальный резерв
страховой компании; c – интенсивность поступления
премий; 
– агрегированные
выплаты требований к моменту 
, 
; 
- независимые
одинаково распределенные случайные величины (ущербы) с функцией распределения 
и средним значением 
, 
при 
; 
– число выплат к
моменту t (пуассоновский процесс с интенсивностью 
).
Известно, что функция вероятности
небанкротства на бесконечном интервале времени 
при начальном
капитале u удовлетворяет
интегральному уравнению:
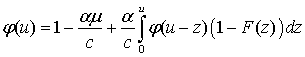(1)
Это уравнение является интегральным
уравнением Вольтерра и допускает аналитическое решение только в частном случае
показательного распределения страховых выплат 
[3]. Поэтому наша работа была посвящена численному нахождению
методом
последовательных приближений, в частности мы рассматриваем гамма-распределение
и распределение Вейбулла в качестве 
. Как известно, правая часть уравнения Вольтерра (1) является
оператором сжатия, поэтому оно имеет единственное решение, которое можно найти
методом последовательных приближений
Пикара.
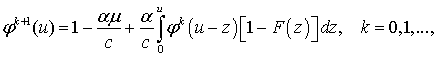
В работе [1] показано, что для рассматриваемого уравнения
Вольтерра (1) сжатие имеет место на каждой итерации с коэффициентом
(2)
равномерно по всем 
, что обеспечивает высокую скорость сходимости при всех 
. Показано, что при старте из начальных функций 
и 
последовательные
приближения монотонно сходятся к решению 
.
На основании теоретически обоснованного в
работе [1] метода последовательных приближений для решения
уравнения вероятности неразорения нами была написана компьютерная программа на
языке Basic, позволяющая находить численные значения решения
этого уравнения для любых начальных параметров и функций распределения,
отвечающим указанному условию для сжатия (2) на каждой итерации, с наперед
заданной точностью.
Но поскольку численное решение этого
уравнения является затратным по времени для современных персональных
компьютеров для больших значений начального капитала, в работе были рассмотрены
аппроксимации вероятности неразорения, такие как аппроксимации
Беекмана-Боуэрса, Де Вильдера и диффузионная. Они строятся из иных соображений,
нежели уравнение для вероятности неразорения, и позволяют находить приближенное
значение вероятности неразорения с меньшими временными затратами.
Для аппроксимации Беекмана-Боуэрса [2]:
,
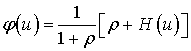(3)
где
.
Идея построения аппроксимационной формулы
заключается в замене 
в формуле (3) гамма-распределением
, первые два момента которого совпадают с моментами 
.
Гамма-распределение имеет вид: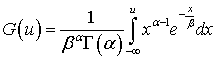 
.
В качестве функции 
, кроме оригинальной в этом случае функции
гамма-распределения, нами использовалась также функция распределения Вейбулла.
Распределение Вейбулла имеет вид: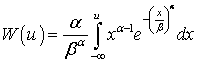 
.
Моменты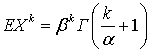 
, 
.
Функция распределения Вейбулла является
обобщением частного случая гамма-распределения и тоже может быть использована
для моделирования поступления требований к страховой компании.
При этом задача нахождения параметров
распределения Вейбулла при известных математическом ожидании и дисперсии не
является столь тривиальной, как для гамма-распределения. С помощью maple, мы
решали систему уравнений, составленную на основании выражений для моментов
функции распределения Вейбулла:
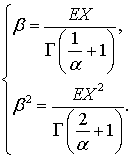
Результаты расчетов для различных
начальных параметров, как значений вероятности неразорения 
, полученных численным
решением уравнения Вольтерра с помощью компьютера, так и приближенных,
полученных с помощью аппроксимаций, а также сравнение результатов между собой
представлены в ряде примеров, один из них приведем здесь.
Пусть выплаты имеют распределение Вейбулла
с математическим ожиданием 
, и дисперсией 
. Пусть также 
, 
.Тогда первые три момента: 
, 
, 
. В таблице приведены значения 
, рассчитанные по методу последовательных приближений,
значения при аппроксимациях, погрешность для этих аппроксимаций.
|
Капитал (u) |
Численное решение |
Аппроксимация Беекмана-Боуэрса |
Аппроксимация Беекмана-Боуэрса |
||
|
|
Вероятность неразорения |
Вероятность неразорения при функции
гамма-распределения |
Относительная погрешность |
Вероятность неразорения при функции Вейбулла |
Относительная погрешность |
|
500 |
0.87291 |
0.87242 |
-0.056% |
0.87453 |
0.186% |
|
600 |
0.91007 |
0.91120 |
0.125% |
0.91267 |
0.285% |
|
700 |
0.93624 |
0.93805 |
0.193% |
0.93892 |
0.287% |
|
800 |
0.95457 |
0.95669 |
0.222% |
0.95711 |
0.266% |
|
900 |
0.96734 |
0.96968 |
0.242% |
0.96978 |
0.253% |
|
1000 |
0.97624 |
0.97875 |
0.256% |
0.97864 |
0.246% |
|
Капитал (u) |
Численное решение |
Диффузионная аппроксимация |
Аппроксимация Де Вильдера |
||
|
|
Вероятность неразорения |
Вероятность неразорения |
Относительная погрешность |
Вероятность неразорения |
Относительная погрешность |
|
500 |
0.87291 |
0.89163 |
2.145% |
0.86930 |
-0.413% |
|
600 |
0.91007 |
0.93052 |
2.247% |
0.90978 |
-0.032% |
|
700 |
0.93624 |
0.95545 |
2.052% |
0.93772 |
0.159% |
|
800 |
0.95457 |
0.97143 |
1.767% |
0.95701 |
0.256% |
|
900 |
0.96734 |
0.98168 |
1.483% |
0.97033 |
0.309% |
|
1000 |
0.97624 |
0.98826 |
1.230% |
0.97952 |
0.335% |
На основании этих и других примеров можно
сказать, что наиболее точной из рассмотренных аппроксимаций является
аппроксимация Де Вильдера. Аппроксимация
Беекмана-Боуэрса дает более точный результат с функцией
гамма-распределения, чем с функцией распределения Вейбулла для небольших
значений начального капитала, причем независимо от функции распределения выплат
. Для больших значений начального капитала аппроксимация Беекмана-Боуэрса дает более точный результат
с функцией распределения Вейбулла, чем с гамма-распределением. Наименее точные
значения получаются при диффузионной аппроксимации. Полученные результаты
позволяют планировать стратегию страховой компании в зависимости от величины
начального капитала.
Литература: