Математика / 4. Прикладная математика
Найко Д. А.1, Найко
Т.І.2
1Вінницький національний аграрний університет
2Вінницький національний технічний університет
Наближення
проміжної похідної комбінаціями операторів
класу В (одновимірний випадок)
Нехай ![]() – множина дійсних
функцій
– множина дійсних
функцій ![]() , визначених та неперервних на
, визначених та неперервних на ![]() і які зростають не
швидше за експоненціальні функції, тобто
і які зростають не
швидше за експоненціальні функції, тобто ![]()
![]() множина функцій
множина функцій ![]() таких, що
таких, що ![]()
![]() множина натуральних
чисел,
множина натуральних
чисел, ![]() .
.
На множині ![]() функцій
функцій ![]() розглянемо лінійний додатний
оператор
розглянемо лінійний додатний
оператор ![]() , який визначено таким чином [Ошибка! Источник ссылки не найден.].
, який визначено таким чином [Ошибка! Источник ссылки не найден.].
Означення. Послідовність ![]() лінійних додатних
операторів вигляду
лінійних додатних
операторів вигляду
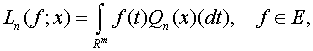 (1)
(1)
![]() деяка область в
деяка область в ![]() , належить класу В, якщо виконуються умови:
, належить класу В, якщо виконуються умови: ![]()
![]() в області
в області ![]() функції
функції ![]() диференційовні; існує симетрична додатно визначена матриця
диференційовні; існує симетрична додатно визначена матриця
![]() така, що
така, що
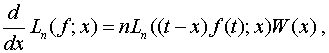
де
функції ![]() аналітичні в області
аналітичні в області ![]() , до того ж
, до того ж
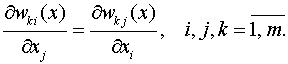
(Матриця
![]() називається інформаційною матрицею і має імовірнісну інтерпретацію. Ми використовуємо позначення
називається інформаційною матрицею і має імовірнісну інтерпретацію. Ми використовуємо позначення
![]() Матриця
Матриця ![]() називається коваріацією).
називається коваріацією).
В даній роботі розглядається
випадок ![]() , тобто оператор (1) – одновимірний.
, тобто оператор (1) – одновимірний.
Прикладами відомих л. д. о., що
належать класу В,
є
многочлени Бернштейна
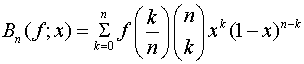 , для яких
, для яких ![]()
оператори Баскакова
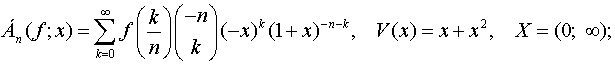 оператори Мірак’яна-Саса
оператори Мірак’яна-Саса
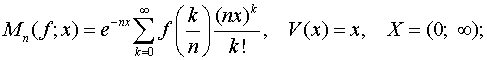
оператори Вейєрштрасса
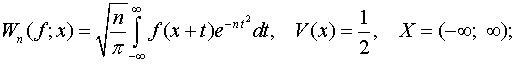
оператори Мюллера-Феллера
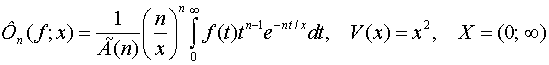
та
інші.
Багато нових прикладів л. д. о.,
що належать класу В,
наводиться в [2] та [3]. Новим, наприклад, є оператор:
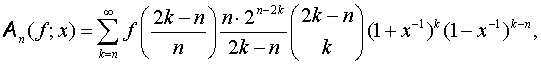
![]() який названо оператором блукань.
який названо оператором блукань.
Розглядатимемо також оператори [1]
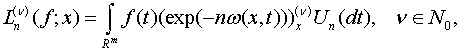
які збігаються з похідними функції ![]() , коли
, коли ![]() не залежить від
не залежить від ![]() і називаються продиференційованими.
і називаються продиференційованими.
Використовуюємо такі позначення:
![]()
![]()
![]()
Доведено [4], що коли ![]() і
і ![]() існує в точці
існує в точці ![]() , то для оператора
, то для оператора ![]() має місце таке
асимптотичне подання
має місце таке
асимптотичне подання
![]()
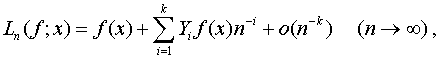 (2)
(2)
де 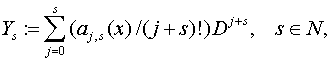 (3)
(3)
(![]() , тобто
, тобто ![]() тотожний оператор;
функції
тотожний оператор;
функції ![]() визначаються рівністю
визначаються рівністю ![]()
причому
![]() коли
коли ![]()
![]() ціла частина
ціла частина
числа
![]() .) Якщо ж
.) Якщо ж ![]() , а
, а ![]() неперервна на
неперервна на ![]() , то (2) виконується рівномірно по
, то (2) виконується рівномірно по ![]() .
.
Використовуючи результати роботи [5], можна довести, що асимптотичну
рівність (2) можна диференціювати при достатній гладкості функції ![]() (див. [6]).
(див. [6]).
Розглянемо такі комбінації операторів класу В.
Нехай 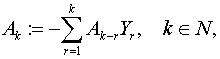 де
де ![]() визначається рівністю
(3),
визначається рівністю
(3), ![]() тотожний оператор. Введемо
лінійний оператор
тотожний оператор. Введемо
лінійний оператор
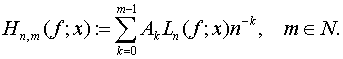 (4)
(4)
Розглянемо лінійний оператор
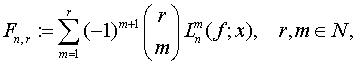 (5)
(5)
де ![]() ,
, ![]() , … ,
, … ,
![]() ,
, ![]() ,
, ![]()
ітеративні лінійні додатні оператори.
Розглянемо лінійний оператор
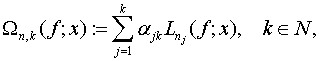 (6)
(6)
де ![]() оператор класу В,
оператор класу В, 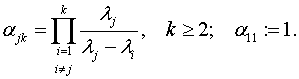
![]()
![]()
![]() різні фіксовані
довільні числа
різні фіксовані
довільні числа ![]() Для зручності ми
покладаємо
Для зручності ми
покладаємо ![]() тоді при
тоді при ![]()
![]()
Лінійна комбінація операторів
класу В
вигляду (6) називається
комбінацією бутцерівського типу.
Через ![]() позначимо будь-який з
операторів (4), (5) або (6). Тоді справедлива така теорема.
позначимо будь-який з
операторів (4), (5) або (6). Тоді справедлива така теорема.
Теорема. Нехай ![]() , а
, а ![]()
![]() Тоді існують
константи
Тоді існують
константи ![]() і
і ![]() такі, що
такі, що
![]()
![]()
де ![]() модуль неперервності
першого порядку функції
модуль неперервності
першого порядку функції ![]() на
на ![]()
Література
1.
Волков Ю. И. Многомерные аппроксимационные операторы, порожденные
мерами Лебега–Стилтьеса // Изв. АН
СССР. Сер. мат. – 1983. – 47, № 3. – С. 435–454.
2.
Волков Ю. И. Новые примеры аппроксимационных линейных положительных
операторов // Методы теории приближения
и их приложения. – Киев: Ин-т математики АН УССР, 1982. – С. 10–19.
3.
Волков Ю. І. Додатні оператори.
Наближення. Ймовірність. – К.: НМК ВО, 1992. – 200 с.
4.
Волков Ю. И. О некоторых линейных положительных операторах //
Мат. заметки. – 1978. – 23, № 5. – С. 659–669.
5.
Найко Д.А. О приближении производных некоторыми комбинациями операторов
класса В //
Укр. мат. журн. –
1987. – 39, №5. – С. 583–587.
6.
Найко Д. А. Обобщение одного асимптотического равенства // Экстремальные
задачи теории приближений и их приложения. – Тезисы докладов респ. конф. 21–31
мая 1990г. – Киев: Ин–т матем. АН УССР. – С.96.