Математика/5. Математическое моделирование

Д.п.н. Монахова Л.Ю.

Военная академия связи, Россия

Операторный подход к определению

математических понятий

Математикам хорошо известна обусловленная традициями двусмысленная ситуация, возникающая при определении числовой функции, когда одним и тем же выражением, например, f(x) обозначается собственно функции, ее аналитического выражения и значения в определенной точке x. Подобная двусмысленность лишь внешне упрощает изложение и, в действительности, не способствует адекватному восприятию понятия функции. Метод преодоления указанных трудностей состоит в использовании фундаментального понятия соответствия между множествами.

Практически все современные учебники рассматривают функцию, обозначаемую f, как однозначное соответствие между множествами, а f(x) трактуется как аналитическое выражение (в общем случае – алгоритм) или значение в точке. На наш взгляд, было бы целесообразно пойти дальше и ввести специальное обозначение для алгоритма, реализующего соответствие, например, в форме:

f(x):= [Описание алгоритма вычисления значений],

в частности,

f(x):= [Аналитическое выражение], допустим, f(x):= sin x.

Подобное нововведение может вызвать возражения по поводу усложнения интуитивно ясных понятий. Однако предлагаемая детализация тезауруса, с одной стороны, зафиксирует семантическое различие рассматриваемых понятий, а, с другой – поможет современным учащимся увидеть связь фундаментальных математических объектов с используемыми в алгоритмических языках операторами.

Впрочем, основное содержание данной статьи связано не с обсуждением обозначений, а с принципом рассмотрения функции как однозначного соответствия, т. е. оператора, определенного на некотором множестве. К сожалению, в силу тех же традиций, указанный разумный подход не получил дальнейшего развития по отношению к другим математическим понятиям таким, как предел последовательности, интеграл, ряд и т. д., несмотря на то что сами операторы дифференцирования, интегрирования и суммирования широко используются в теории. Обычным объяснением служит ссылка на якобы чрезмерную сложность перечисленных понятий, хотя, как нетрудно видеть, все они укладываются в ту же схему, что и определение функции, и, значит, будут лишь способствовать закреплению указанного единого подхода. В то же время, издержки, обусловленные традиционными дефинициями, довольно велики. Достаточно сравнить два определения, по сути, одинаковых понятий несобственного интеграла и ряда в учебнике Л.Д.Кудрявцева “Курс математического анализа. Ч. 1” (с. 512 и с. 545) или вдуматься в определение ряда как “выражения вида …”.

Опыт преподавания математики в ВАС убеждает в возможности единого операторного подхода к изложению основных математических понятий. Первым (после определения функции) весьма типичным основным понятием служит предел числовой последовательности. Предлагается использовать следующий шаблон для такого рода определений.

Определение 1. Число a называется значением предела последовательности (x_n), если для любого положительного числа e существует такое число N, что для любых n>N выполняется неравенство

| x_n - a|<e , т.е.

[a – предел последовательности (x_n)] º ("e > 0)($N)("n > N)[| x_n - a|<e].

После доказательства теоремы о единственности предела последовательности можно дать следующее определение.

Определение 2. Оператором предела последовательности называется однозначное соответствие, обозначаемое , которое числовой последовательности сопоставляет значение ее предела.

Запись означает, что числовая последовательность (x_n) принадлежит области определения оператора предела, и число a является значением предела последовательности (x_n), или, короче, пределом последовательности.

Алгоритм, определяющий оператор предела, может быть представлен в форме:

.

Таким образом, определение предела последовательности укладывается в ту же схему, что и определение функции. Будет полезно отметить, что областью определения оператора предела служит множество сходящихся последовательностей, поэтому формальную запись можно рассматривать в том же смысле, что и , а именно, как применение оператора к аргументу, не принадлежащему области определения.

Опуская аналогичные определения для производной, интеграла и несобственного интеграла, остановимся на понятии числового ряда, так как именно с ним связаны серьезные дидактические проблемы. Операторный подход позволяет естественным образом обойти эти трудности с помощью следующей системы определений.

Определение 3. Число s называется суммой числовой последовательности (ряда) с общим членом u_n, если оно равно значению предела последовательности частичных сумм s_n = u₁ + u₂ + … + u_n , т.е.

.

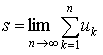Определение 4. Оператором числового ряда с общим членом u_n называется однозначное соответствие, обозначаемое , которое числовой последовательности (u_n) сопоставляет сумму последовательности с общим членом u_n.

Таким образом, запись вида 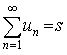означает, что последовательность (u_n) принадлежит области определения оператора числового ряда (т.е. ряд сходится) и сумма ряда равна s.

Алгоритм, определяющий оператор числового ряда, имеет вид:

,

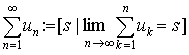где понимается в указанном выше смысле (см. Определение 2).

Вопрос о сходимости числовых рядов сводится к выяснению принадлежности последовательности (u_n) области определения оператора числового ряда.

Нетрудно видеть, что приведенные примеры определений аналогичны друг другу и в такой форме переносятся на многие другие понятия анализа. Использование единой операторной формы должно, на наш взгляд, способствовать систематизации знаний, а многократное ее повторение обеспечит прочное усвоение. Наконец, внешнее сходство рассматриваемых операторов с конструкциями алгоритмических языков поможет учащимся, формирующимся в условиях всеобщей информатизации, адекватно воспринимать сложные математические понятия.