Економічні науки/ 8. Математичні методи в економіці

Савчук А.В.

Науковий керівник: асистент Настасій О.Б.

Буковинська державна фінансова академія, Україна

Рахунки ренти

Майже вся частина населення держав  з ринковою економікою живе за рахунок ренти, тобто регулярно протягом певного періоду одержують раніше обумовлену величину коштів з відповідного рахунка в банку або страховій компанії. Цей вид отримання коштів є дуже вигідним для всіх верств населення. Економіка займається якраз тим, що вона, застосовуючи певні математичні дії й формули, розраховує й визначає скільки коштів треба покласти на рахунок ренти для того, щоб виконувались відповідні умови.

Розглянемо загальний випадок ренти. Позначимо через А величину внеску на рентний рахунок. Нехай з цього рахунку роблять виплати розміром Р регулярно, з постійним періодом часу протягом n періодів, починаючи через один після відкриття рахунка ренти. Нехай величина внеску зростає кожного періоду на R відсотків. Щоб отримати першу виплату у розмірі  Р після першого періоду часу треба вкласти в рахунок ренти таку кількість коштів А1, яка задовольняє рівність

А1(1+і) = Р,                                               (2)

де      і = .

З цієї рівності знаходимо значення  А1 вигляду

А1 = Р(1+і.                                              (3)

Аналогічно знаходимо внесок  А2, який зростає до Р після двох періодів часу

А2 = Р(1+і,                                           (4)

а також частину внеску Аn, яка зростає до Р після n періодів

Аn = Р(1+і.                                            (5)

Загальна величина внеску А на рахунок ренти є сумою

А = А1 + А2 + …+Аn = Р(1+і + Р(1+і + ….+ Р(1+і.      (6)

тобто А – це сума геометричної прогресії  n членів, перший член якої                b1 =P(1+і, а знаменник q =(1+і.

Тому

А = 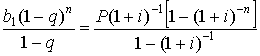                            (7)

Спростивши останній дріб шляхом множення чисельника і знаменника на (1+і) одержимо:

А = [1−(1+i                                      (8)

Фінансисти використовують формулу (8) у вигляді

А = ,                                         (9)

де   =  [1 – (1+i табульована для різних значень  і = та n.

Література:

1. Грисенко М.В., Математика для економістів: Методи й моделі, приклади й задачі: Навч. посібник. – К. Либідь, 2007. – 720с.

2. Травкін Ю.І., Малярець Л.М. Математика для економістів: Підручник. – Х.: ВД «ІНЖЕК» 2005. – 816с.

3. Дюженкова Л.І., Дюженкова О.Ю., Михалін Г.О. Вища математика: Приклади і задачі / Посібник. – К.: Видавничий центр «Академія»,     2003. – 624с.

4. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. – К.: Видавництво А.С.К., 2004. – 648с.

5.  Барковська Н.В., Барковський В.В. Вища математика для економістів . – Київ :ЦУЛ, 2002.- 400с.