Экономические науки/2. Математические методы в экономике

Максименко К. Є.

Національний технічний університет України «КПІ», Україна

Магістральна теорія для динамічної моделі Леонтьєва з термінальним критерієм

Одним з видів моделей, що описують міжгалузеву організацію виробництва на рівні країни чи регіону є лінійні динамічні моделі типу Леонтьєва. Як відомо, при зведенні таких моделей до задач лінійного програмування відповідний розширений фазовий простір набуває розмірності nT, де n – це розмірність технологічної матриці, а T – довжина часового проміжку, яка може бути дуже великою. Це фактично унеможливлює застосування стандартних процедур лінійного програмування до підрахунку точної оптимальної траєкторії.

Тому були здійснені спроби дослідити ту чи іншу математичну модель якісними методами. В результаті було створено магістральну теорію. Нижче приведене формулювання самої задачі оптимізації та результати магістральної теорії щодо неї.

Розглянемо економіку з n чистими галузями. Нехай А – нерозкладна, невід’ємна, квадратна матриця міжгалузевого балансу, Ах – вектор витрат. Валовий випуск в період Т використовується як запас сировини для виробничого циклу в наступний період. Ураховуючи ресурсне обмеження отримаємо таку оптимізаційну задачу:

(1)

де х0 – початковий запас сировини, с – заданий n-вимірний вектор цін.

Дана модель називається динамічною моделлю Леонтьєва. Оптимальна задача є стандартною задачею лінійного програмування.

Запишемо ресурсні обмеження моделі у розгорнутому вигляді:

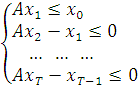
В матричній формі дану задачу можна представити так:

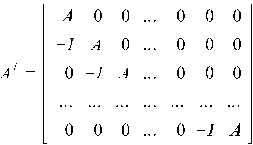
Символи А, -І, 0 означають квадратні блоки розміром n×n. Із використанням введених позначень задача набуває вигляду:

Для початку введемо функцію :

де - евклідова норма в . Назвемо дану функцію квазіметрикою. Вона є виміром кутової відстані між векторами x та y.

Введемо поняття магістралі для нашої задачі.

Означення. Промінь

є магістраллю задачі (1), якщо такі, що для будь-якої оптимальної траєкторії отримуємо

Щоб застосувати до даної задачі теореми про магістраль, накладемо такі обмеження: , А – нерозкладна і примітивна матриця. Відповідно матриця А є і стійкою.

Позначимо як правий вектор Фробеніуса матриці А. Тоді має силу така теорема:

Теорема (про магістраль для динамічної моделі Леонтьєва). При даних умовах, вектор Фробеніуса є магістраллю для задачі (1).

Тобто ця теорема говорить, що оптимальна траєкторія задачі, (1) при досить великому Т, на певному часовому проміжку лежить дуже близько до магістралі, що є вектором Фробеніуса матриці А.

Наведену теорему називають теоремою Морішими.

При досліджені даної теорії мною було виведено декілька тверджень, що значно розширюють результати даної теорії щодо лінійної динамічної моделі Леонтьєва з термінальним критерієм. Нижче вони наведені без доведення:

1) Задачу оптимізації (1) можна замінити задачею:

Таким чином ми визначаємо оптимальний випуск в останній період. Випуск в інші періоди знаходиться простим множенням на матрицю:

2) На відміну від теореми Морішими можна стверджувати, що при досить великому Т оптимальна траєкторія задачі (1) починається близько до магістралі і поступово віддаляється від неї. Тобто ми позбулися початкового періоду відхилення від магістралі оптимальної траєкторії, існування якого зазначалося в теоремі.

Література:

1. Пономаренко О.І., Перестюк М. О., Бурим В. М. Сучасний економічний аналіз, Ч. 2. Макроекономіка – К.: Вища шк., 2004. – 207 с: іл. – ISBN 966-642-251-4

2. Аллен Р. Математическая экономия. – М.: Изд-во иностр. лит., 1963. –668 с.