К. ф.-м. н. Долгарев А.И.
Пензенский
государственный университет
Натуральные
уравнения галилеевой кривой
и решение уравнения Ньютона
для движения с двумя степенями свободы
Механическое движение
материальной точки с двумя степенями свободы происходит во времени по
траектории:
![]() =
= ![]() ,
, ![]() ,
,
параметр ![]() есть время,
принимающее действительные значения. Ускорение движения точки описывается
функцией
есть время,
принимающее действительные значения. Ускорение движения точки описывается
функцией
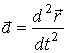 =
= ![]() .
.
Функция ![]() задается не только в
каждой точке траектории
задается не только в
каждой точке траектории ![]() , но и в каждой точке некоторой области на евклидовой
плоскости
, но и в каждой точке некоторой области на евклидовой
плоскости ![]() =
= ![]() , определяемой любой точкой
, определяемой любой точкой ![]() траектории и
базисными векторами
траектории и
базисными векторами ![]() плоскости. Возникает
обратная задача: нахождение траектории движущейся точки в заданном векторном
поле ускорения. Это задача И. Ньютона. Анализу ситуации в решении задачи И.
Ньютона посвящена книга В.И. Арнольда [1]. Указанная задача относится к механике
Галилея-Ньютона. В книге [1, c. 12 – 14] описано пространство-время Галилея
плоскости. Возникает
обратная задача: нахождение траектории движущейся точки в заданном векторном
поле ускорения. Это задача И. Ньютона. Анализу ситуации в решении задачи И.
Ньютона посвящена книга В.И. Арнольда [1]. Указанная задача относится к механике
Галилея-Ньютона. В книге [1, c. 12 – 14] описано пространство-время Галилея ![]() как прямая сумма оси
времени и 3-мерного евклидова пространства
как прямая сумма оси
времени и 3-мерного евклидова пространства ![]() . Определено
. Определено ![]() на основе аффинного
пространства
на основе аффинного
пространства ![]() . Соответственно, 3-мерное пространство-время есть
. Соответственно, 3-мерное пространство-время есть ![]() =
= ![]() , при этом
, при этом ![]() есть
есть ![]() . Естественно в решении
задачи И. Ньютона о движении с двумя степенями свободы воспользоваться методами
геометрии Галилея 3-мерного пространства-времени. Однако геометрия Галилея
размерности 3 ко времени написания книги [1] не была разработана. Рассматривая
методы решения задачи В.И. Арнольд приходит к следующему выводу: «Анализ общей
потенциальной системы с двумя степенями свободы выходит за рамки возможностей
современной науки», [1, с. 26, аннотация к § 5].
. Естественно в решении
задачи И. Ньютона о движении с двумя степенями свободы воспользоваться методами
геометрии Галилея 3-мерного пространства-времени. Однако геометрия Галилея
размерности 3 ко времени написания книги [1] не была разработана. Рассматривая
методы решения задачи В.И. Арнольд приходит к следующему выводу: «Анализ общей
потенциальной системы с двумя степенями свободы выходит за рамки возможностей
современной науки», [1, с. 26, аннотация к § 5].
Пусть
точка ![]() плоскости Евклида
плоскости Евклида ![]() рассматривается в момент времени
рассматривается в момент времени ![]() . Это означает, что имеется событие
. Это означает, что имеется событие ![]() 3-мерного пространства-времени
Галилея
3-мерного пространства-времени
Галилея ![]() . С течением времени событие
. С течением времени событие ![]() изменяется, мировая
линия события
изменяется, мировая
линия события ![]() есть
есть
![]() =
= ![]() ,
, ![]() . (1)
. (1)
Кривые в пространстве-времени ![]() изучаются в [2, c. 46 – 101; 3]. Ниже предлагается решение в общем
случае задачи И. Ньютона средствами геометрии Галилея.
изучаются в [2, c. 46 – 101; 3]. Ниже предлагается решение в общем
случае задачи И. Ньютона средствами геометрии Галилея.
1.Элементы геометрии Галилея
1.1. Пространство-время Галилея
Укажем
необходимые понятия и факты геометрии Галилея 3-мерного пространства-времени из
[2]. Пусть ![]() аффинное пространство,
аффинное пространство,
![]() над
над ![]() – его линейное пространство.
Галилеевым скалярным произведением векторов
– его линейное пространство.
Галилеевым скалярным произведением векторов ![]() и
и ![]() называется число
называется число ![]() , определяемое равенствами
, определяемое равенствами
![]() =
= 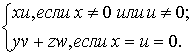 (2)
(2)
Галилеевым скалярным квадратом вектора ![]() является
является
![]() =
= 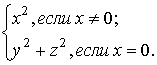
Галилеева норма
вектора ![]() равна
равна
![]() =
= 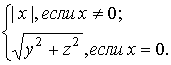 (3)
(3)
Б.А. Розенфельд относит нормы,
определяемые двумя равенствами, к квазинормам, [3, с. 369]. В связи с этим,
галилеева норма (3) вектора ![]() является квазинормой.
является квазинормой.
Линейное
пространство ![]() с галилеевым
скалярным произведением векторов (2) называется галилеевым векторным
пространством и обозначается
с галилеевым
скалярным произведением векторов (2) называется галилеевым векторным
пространством и обозначается ![]() . Компонента
. Компонента ![]() всякого вектора
всякого вектора ![]() из
из ![]() называется временной,
компоненты
называется временной,
компоненты ![]() вектора
вектора ![]() называются
пространственными. Векторы
называются
пространственными. Векторы ![]() ,
, ![]() , называются галилеевыми, а векторы
, называются галилеевыми, а векторы ![]() называются
евклидовыми; норма вектора
называются
евклидовыми; норма вектора ![]() является евклидовой,
см. (3). Скалярное произведение галилеева вектора
является евклидовой,
см. (3). Скалярное произведение галилеева вектора ![]() ,
, ![]() , и евклидова вектора
, и евклидова вектора ![]() , по (2), равно нулю. Поэтому всякий евклидов вектор
перпендикулярен всякому галилееву
вектору.
, по (2), равно нулю. Поэтому всякий евклидов вектор
перпендикулярен всякому галилееву
вектору.
Обозначим:
![]() . Имеется разложение
. Имеется разложение
![]() .
.
Упорядоченное множество Б =![]() является базисом пространства
является базисом пространства ![]() , базис Б ортонормирован.
Вектор
, базис Б ортонормирован.
Вектор ![]() временной,
временной, ![]() пространственные.
пространственные.
Аффинное
пространство ![]() , в линейном пространстве
, в линейном пространстве ![]() которого определено
галилеево скалярное произведение векторов, становится пространством-временем
Галилея и обозначается
которого определено
галилеево скалярное произведение векторов, становится пространством-временем
Галилея и обозначается ![]() . Точки аффинного пространства становятся точками пространства
Галилея и называются еще событиями. Пространство событий
. Точки аффинного пространства становятся точками пространства
Галилея и называются еще событиями. Пространство событий ![]() есть мир. Прямые и
плоскости аффинного пространствами становятся прямыми и плоскостями мира
есть мир. Прямые и
плоскости аффинного пространствами становятся прямыми и плоскостями мира ![]() . Кривая
. Кривая ![]() =
= ![]() аффинного пространства,
проходящая через точку
аффинного пространства,
проходящая через точку ![]() , называется мировой линией точки
, называется мировой линией точки ![]() . Репер В =
. Репер В = ![]() пространства Галилея
является ортонормированным. Координаты события
пространства Галилея
является ортонормированным. Координаты события ![]() в репере В – это координаты вектора
в репере В – это координаты вектора ![]() в базисе Б. Вектор
в базисе Б. Вектор ![]() репера В является временным, остальные векторы
репера В пространственные. Пространственное
направление в пространстве-времени
репера В является временным, остальные векторы
репера В пространственные. Пространственное
направление в пространстве-времени ![]() определяется евклидовым
вектором
определяется евклидовым
вектором ![]() . Время в пространстве Галилея 1-мерно. Направление во
времени есть направление в будущее или направление в прошлое. Два различных галилеевых
вектора
. Время в пространстве Галилея 1-мерно. Направление во
времени есть направление в будущее или направление в прошлое. Два различных галилеевых
вектора ![]() ,
, ![]() ,
, ![]() ,
, ![]() , задают в пространстве Галилея одно и то же временное
направление, если их временные компоненты имеют один и тот же знак. Оба вектора
определяют направление в будущее, если
, задают в пространстве Галилея одно и то же временное
направление, если их временные компоненты имеют один и тот же знак. Оба вектора
определяют направление в будущее, если ![]() ; и определяют направление в прошлое, если
; и определяют направление в прошлое, если ![]() . Выбор галилеева вектора
. Выбор галилеева вектора ![]() определяет выбор
временного направления в пространстве Галилея.
определяет выбор
временного направления в пространстве Галилея.
Вместе
с событием ![]() рассматривается
множество событий
рассматривается
множество событий ![]() , одновременных с событием
, одновременных с событием ![]() ; у всех этих событий совпадают временные компоненты.
Множество событий, одновременных с
; у всех этих событий совпадают временные компоненты.
Множество событий, одновременных с ![]() , есть евклидова плоскость
, есть евклидова плоскость
![]()
пространства-времени Галилея. Выполняется
1. Свойство.
Через всякую точку пространства Галилея
проходит единственная евклидова плоскость.
Все евклидовы плоскости
пространства Галилея параллельны.
Во всякой точке ![]() пространства-времени
Галилея направление во времени определяется выбором открытого полупространства,
границей которого является евклидова плоскость, проходящая через точку
пространства-времени
Галилея направление во времени определяется выбором открытого полупространства,
границей которого является евклидова плоскость, проходящая через точку ![]() .
.
Все плоскости пространства-времени
Галилея, отличные от евклидовых плоскостей, есть плоскости Галилея, это
2-мерные галилеевы пространства.
1.2. Кривые в пространстве Галилея
Кривая
![]() называется регулярной
класса
называется регулярной
класса ![]() , если функция
, если функция ![]() не менее трех раз
дифференцируема,
не менее трех раз
дифференцируема, ![]() и векторы
и векторы ![]() ,
, ![]()
![]() неколлинеарны.
Компоненты
неколлинеарны.
Компоненты ![]() кривой (1) трижды дифференцируемы. Имеем:
кривой (1) трижды дифференцируемы. Имеем:
![]() ,
, ![]() ;
;
![]() , вектор
, вектор ![]() евклидов. Согласно [2.
c. 56 – 57], параметризация (1) галилеевой кривой
является естественной. Касательная
евклидов. Согласно [2.
c. 56 – 57], параметризация (1) галилеевой кривой
является естественной. Касательная ![]() к кривой (1) в точке
к кривой (1) в точке ![]() определяется вектором
определяется вектором
![]() и не зависит от
параметризации кривой. Кривизна
и не зависит от
параметризации кривой. Кривизна ![]() кривой (1) равна норме
вектора производной второго порядка
кривой (1) равна норме
вектора производной второго порядка
![]() . (4)
. (4)
Имеем функцию кривизны
![]() .
.
Обозначим через ![]() единичный вектор
направления
единичный вектор
направления ![]() , тогда
, тогда
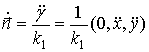 .
.
Производная единичного
евклидова вектора ![]() равна
равна
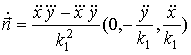 . (5)
. (5)
Вектор
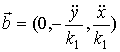
является единичным, ![]() , величина
, величина
![]() =
= 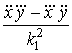 (6)
(6)
называется кручением галилеевой кривой
(1). Вектор ![]() теперь записывается в
виде
теперь записывается в
виде ![]() =
= ![]() . По [2, c. 59 – 61],
кручение
. По [2, c. 59 – 61],
кручение ![]() кривой (1) есть
каппа-функция евклидова вектора
кривой (1) есть
каппа-функция евклидова вектора ![]() . Функция кривизны
. Функция кривизны
![]()
кривой отыскивается по формуле (6).
1.3. Натуральные уравнения галилеевой кривой
По
формулам (4) и (6) кривизны и кручения галилеевой кривой (1) получаем систему
обыкновенных дифференциальных уравнений
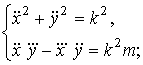
![]() .
(7)
.
(7)
Считая функции
кривизны и кручения
![]() (8)
(8)
заданными, отыскиваем функции ![]() – компоненты задания
галилеевой кривой (1)
– компоненты задания
галилеевой кривой (1) ![]() =
= ![]() . Кривая (1) однозначно определяется начальными условиями
. Кривая (1) однозначно определяется начальными условиями
![]() ,
, ![]() , (9)
, (9)
выделяется линия, проходящая через точку ![]() в направлении вектора
касательной
в направлении вектора
касательной ![]() . В [2] рассмотрен только случай, в котором
. В [2] рассмотрен только случай, в котором ![]() и
и ![]() постоянны.
постоянны.
2.Теорема. Компоненты ![]() кривой (1) являются решением системы обыкновенных дифференциальных
уравнений (7) при условии, что функции кривизны и кручения (8) кривой заданы.
Начальные условия (9) определяют единственную кривую (1), проходящую через
заданную точку
кривой (1) являются решением системы обыкновенных дифференциальных
уравнений (7) при условии, что функции кривизны и кручения (8) кривой заданы.
Начальные условия (9) определяют единственную кривую (1), проходящую через
заданную точку ![]() в направлении вектора касательной
в направлении вектора касательной ![]() .
.
# В первом уравнении
системы (7) обозначим
![]() . (10)
. (10)
При дифференцировании функций ![]() для второго уравнения системы (7) понадобится
производная
для второго уравнения системы (7) понадобится
производная
![]() .
.
Проверка показывает, что функции ![]() из (10) удовлетворяют
и второму уравнению системы (7). Поэтому функции
из (10) удовлетворяют
и второму уравнению системы (7). Поэтому функции ![]() являются решениями
дифференциальных уравнений из (10). Кривизна и кручение всех найденных кривых
являются решениями
дифференциальных уравнений из (10). Кривизна и кручение всех найденных кривых ![]() =
= ![]() совпадают с заданными
функциями (8). Начальные условия (9) выделяют из 4-параметрического семейства
решений единственную кривую
совпадают с заданными
функциями (8). Начальные условия (9) выделяют из 4-параметрического семейства
решений единственную кривую ![]() (1). #
(1). #
Функции
(8) называются натуральными уравнениями кривой.
3.Следствие.
[2, c. 66 – 67]. Если
кривизна и кручение кривой (1) постоянны,
то кривая (1) является винтовой линией
g(t) = 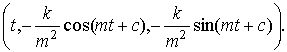 (11)
(11)
#
Интегрируя уравнения (10) при ![]() , имеем
, имеем
![]()
заменяя репер пространства Галилея ![]() , можно получить
, можно получить ![]() ,
, ![]() . Проекция кривой (11) на евклидову плоскость есть
. Проекция кривой (11) на евклидову плоскость есть
![]() (t) =
(t) = 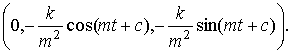
Это евклидова окружность с центром в
начале отсчета и радиусом ![]() ,
,
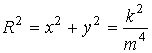 .
.
Образующая цилиндра, на которой лежит
винтовая линия (11), параллельна временной оси ![]() . #
. #
1.4. Примеры получения кривых по натуральным
уравнениям
Пример 1. Заданы функции кривизны и кручения
линии:
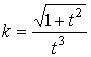 ,
, ![]() .
.
Функция ![]() , согласно третьему равенству из (10), есть
, согласно третьему равенству из (10), есть
![]() .
.
Тогда по (10):
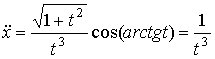 ,
, 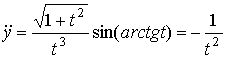 .
.
В результате двукратного интегрирования
имеем семейство кривых – мировых линий движения точек
![]() =
= ![]() ,
,
начальные условия ![]() выделяют кривую
выделяют кривую
![]() =
= ![]() ,
,
траектория движения материальной точки ![]() =
= ![]() есть цепная линия,
[5, № 90].
есть цепная линия,
[5, № 90].
Пример 2.
Натуральные уравнения кривой есть
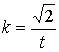 ,
, ![]() .
.
По (10) находим,
![]() .
.
Согласно (10) имеем дифференциальные
уравнения:
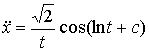 ,
, 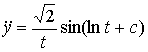 .
.
Первое интегрирование дает:
![]() ,
, ![]() .
.
В результате замены ![]() приходим к выражениям
приходим к выражениям
![]() ,
, ![]() ;
;
тогда пространственные составляющие мировой
линии:
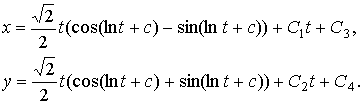
Рассмотрим
альтернативное решение. Используя разложение
![]() ,
,
можно принять
![]() . (12)
. (12)
При этом выполняются соотношения:
![]() и
и ![]() ,
,
то есть функции (12) удовлетворяют второму уравнению системы (7).
Интегрируя дважды выражения (12), получаем
![]() ,
, ![]() .
.
Эти значения проще, чем полученные ранее.
При начальных условиях ![]() имеем галилееву
кривую
имеем галилееву
кривую
![]() =
= ![]() ,
,
с евклидовой проекцией:
![]() =
= ![]() .
.
Получились две различные параметризации
одной кривой – два разных закона движения точки по траектории. Различные
колебания, суммируясь, дают одну и туже траекторию движения точки.
В
последней функции выполним замену ![]() , тогда
, тогда ![]() . Получаем пространственную кривую
. Получаем пространственную кривую ![]() =
= ![]() . Заменим обозначение параметра
. Заменим обозначение параметра ![]() на
на ![]() :
:
![]() =
= ![]() .
.
Это коническая спираль, [5, № 420]. Если
смысл параметра ![]() в задании мировой
линии движения
в задании мировой
линии движения ![]() =
= ![]() есть время, то
имеется движение точки с двумя степенями свободы с законом
есть время, то
имеется движение точки с двумя степенями свободы с законом ![]() =
= ![]() .
.
Пример 3.
Заданы натуральные уравнения галилеевой линии
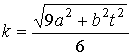 ,
, ![]() .
.
Возьмем разложение функции ![]() в сумму квадратов:
в сумму квадратов: ![]() =
= ![]() +
+ ![]() . Функции
. Функции ![]() ,
, ![]() удовлетворяют и
второму уравнению системы (7). Общие интегралы выбранных уравнений таковы:
удовлетворяют и
второму уравнению системы (7). Общие интегралы выбранных уравнений таковы:
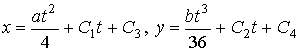 .
.
Начальные условия ![]() в случае
в случае ![]() выделяют функции
выделяют функции ![]() . Получена галилеева кривая:
. Получена галилеева кривая:
![]() =
= ![]() ,
,
ее евклидова проекция есть ![]() =
= ![]() или
или ![]() – полукубическая парабола.
– полукубическая парабола.
2. Решение уравнения И. Ньютона в движении
с двумя степенями свободы
2.1. Поле ускорений и траектория движения
Пусть
на евклидовой плоскости задано векторное поле
![]() ,
, ![]() ,
,
которое считаем полем ускорений движущееся
материальной точки. Траектория движения точки описывается функцией
![]() =
= ![]() .
.
В каждой точке ![]() траектории вектор
ускорения есть
траектории вектор
ускорения есть
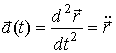 .
.
Величина ускорения равна
![]() . (13)
. (13)
Мировая линия движения материальной точки
с учетом времени есть:
![]() =
= ![]() =
= ![]() +
+![]() ,
,
где ![]() единичный вектор
времени. Функция ускорения движения по траектории
единичный вектор
времени. Функция ускорения движения по траектории ![]() такова
такова
![]() =
= ![]() =
= ![]() .
.
Кривизна мировой линии движения есть ![]() , см. (4). Уравнение И. Ньютона для движения материальной
точки по траектории
, см. (4). Уравнение И. Ньютона для движения материальной
точки по траектории ![]() имеет вид (в наших
обозначениях):
имеет вид (в наших
обозначениях):
![]() ,
,
см. [1, равенство (1)]. Траектория
движения ![]() , скорость
, скорость ![]() являются функциями
времени. Сила
являются функциями
времени. Сила ![]() , под воздействием которой движется материальная точка, есть
функция времени
, под воздействием которой движется материальная точка, есть
функция времени ![]()
![]()
и уравнение И. Ньютона записывается в виде
![]() =
= ![]() ,
,
где ![]() заданная сила,
действующая на материальную точку как ускорение движения точки. И решением
уравнения И. Ньютона является траектория движения точки
заданная сила,
действующая на материальную точку как ускорение движения точки. И решением
уравнения И. Ньютона является траектория движения точки ![]() , тоже функция времени.
, тоже функция времени.
2.2. Отыскание траектории движения
Для
получения галилеевой линии в ![]() нужно знать функции
кривизны и кручения линии, см. теорему 2. По полю ускорения
нужно знать функции
кривизны и кручения линии, см. теорему 2. По полю ускорения ![]() движения определяется
кривизна
движения определяется
кривизна ![]() , (13). Компоненты
, (13). Компоненты ![]() вектора ускорения
вектора ускорения ![]() позволяют найти кручение
мировой линии движения точки
позволяют найти кручение
мировой линии движения точки
![]() =
= 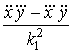 =
= ![]() , (14)
, (14)
см. (6). Согласно теореме 2, мировая линия
движения точки однозначно определяется с точностью до положения в пространстве
Галилея, а следовательно, однозначно определяется траектория движения точки.
Тем самым решается уравнение И. Ньютона для механического движения с двумя степенями
свободы.
4.Теорема. Компоненты ![]() траектории движения точки
траектории движения точки ![]() однозначно определяются, если задано поле ускорений
однозначно определяются, если задано поле ускорений ![]() точки
точки ![]() ; кривизна и ускорение
мировой линии
; кривизна и ускорение
мировой линии ![]() движения вычисляются по формулам (13) и (14), которые задают правые
части обыкновенных дифференциальных уравнений системы (7). Уравнение И. Ньютона
сводится к решению системы обыкновенных дифференциальных уравнений вида (7).
Начальные условия (9) выделяют траекторию движения точки
движения вычисляются по формулам (13) и (14), которые задают правые
части обыкновенных дифференциальных уравнений системы (7). Уравнение И. Ньютона
сводится к решению системы обыкновенных дифференциальных уравнений вида (7).
Начальные условия (9) выделяют траекторию движения точки ![]() в направлении вектора
в направлении вектора ![]() .
.
# Мировая линия ![]() движения точки
движения точки ![]() , согласно теореме 2, отыскивается по функциям кривизны и
кручения (13) и (14), найденным по компонентам векторного поля ускорения
, согласно теореме 2, отыскивается по функциям кривизны и
кручения (13) и (14), найденным по компонентам векторного поля ускорения ![]() . Компоненты
. Компоненты ![]() траектории зависят от
функций
траектории зависят от
функций ![]() и
и ![]() , см. (10).
Траектория движения
, см. (10).
Траектория движения ![]() проходит через
заданную в (9) точку
проходит через
заданную в (9) точку ![]() в направлении вектора
касательной
в направлении вектора
касательной ![]() . #
. #
Как показывают теоремы
2 и 4, компоненты ![]() и
и ![]() траектории
траектории ![]() точки
точки ![]() отыскиваются все-таки
по дифференциальным уравнениям
отыскиваются все-таки
по дифференциальным уравнениям
![]() и
и ![]() .
.
Теорема 4 обосновывает такой способ
отыскания траектории движения.
2.3. Примеры решения уравнения И. Ньютона
Пример 1. Задано поле ускорений
![]() =
= ![]() ,
, ![]() .
.
Находим по (13) и (14): 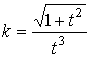 ,
, ![]() . В п. 1.4, пример 1, получена мировая линия движения
. В п. 1.4, пример 1, получена мировая линия движения ![]() =
= ![]() с найденными кривизной
и кручением, траектория движения материальной точки
с найденными кривизной
и кручением, траектория движения материальной точки ![]() =
= ![]() есть цепная линия.
есть цепная линия.
В
евклидовой геометрии, например, плоская кривая ![]() в естественной параметризации
отыскивается по функции кривизны, [6, c. 137 –
143]. Кривизна линии есть модуль вектора производной второго порядка
в естественной параметризации
отыскивается по функции кривизны, [6, c. 137 –
143]. Кривизна линии есть модуль вектора производной второго порядка ![]() . Но естественный параметр
. Но естественный параметр ![]() евклидовой кривой не
является временем и
евклидовой кривой не
является временем и ![]() не является вектором
ускорения движения точки по траектории
не является вектором
ускорения движения точки по траектории ![]() . Методы галилеевой геометрии позволили решить уравнение И.
Ньютона, т.к. естественным параметром галилеевой кривой является время.
. Методы галилеевой геометрии позволили решить уравнение И.
Ньютона, т.к. естественным параметром галилеевой кривой является время.
Пример 2. Поле ускорения движения есть
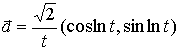 .
.
По (13) и (14) имеем: 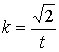 ,
, ![]() . В примере 2 п.1.4:
. В примере 2 п.1.4: ![]() =
= ![]() , траектория движения:
, траектория движения: ![]() =
= ![]() .
.
Пример 3. Поле ускорений:
![]() .
.
Находим: 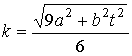 ,
, ![]() . В примере 3 из 1.4 найдена мировая линия движения
. В примере 3 из 1.4 найдена мировая линия движения ![]() =
= ![]() , траектория точки:
, траектория точки: ![]() =
= ![]() или
или ![]() – полукубическая парабола.
– полукубическая парабола.
Литература:
1.
Арнольд, В.И.
Математические методы классической механики./В.И. Арнольд. – М.: Наука,
1989. – 472с.
2.
Долгарев А. И.
Классические методы в дифференциальной геометрии одулярных пространств.
Монография./ А.И. Долгарев. – Пенза: ИИЦ ПГУ, 2005.- 306с.
3.
Долгарев, А.И. Элементы дифференциальной галилеевой геометрии
и одуль галилеевых преобразований./ А.И. Долгарев. – Саранск: Средневолжское
математическое общество, 2003, препринт 63. – 116с.
4.
Розенфельд Б.А.,
Замаховский М.П. Геометрия групп Ли. Симметрические, параболические и
периодические пространства. – М.: МЦНМО, 2003.- 560с.
5.
Савелов А. А. Плоские кривые./ А.А. Савелов. – М.:
Физматгиз, 1960. – 294с.
6. Рашевский П.К. Курс дифференциальной геометрии./ П.К. Рашевский. – М.: Гостехиздат, 1956. 420с.