Шилинец В.
А., Рылова А.С.
Белорусский
государственный педагогический университет
ИСПОЛЬЗОВАНИЕ МОНОГЕННЫХ В СМЫСЛЕ
В.С. ФЕДОРОВА ФУНКЦИЙ ПРИ РЕШЕНИИ КРАЕВЫХ ЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ФОРМАЛЬНЫХ ПРОИЗВОДНЫХ
Предметом
исследования в данной работе является следующая система дифференциальных
уравнений в частных производных:
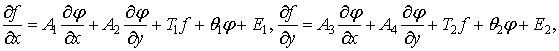
где 
(
(
) – искомые (известные) комплексные функции от 
класса 
(
),
.
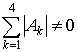Через
обозначаем класс
комплексных функций от 
, имеющих непрерывные частные производные до 
–го порядка включительно в некоторой односвязной области 
плоскости 
.
Как
показано в работе [1], данная система эквивалентна системе в формальных производных
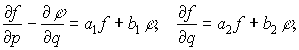(1)
(
– известные функции класса 
(
) при следующем необходимом и достаточном условии:
,
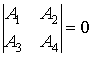где формальные производные 
, 
определяются
следующим образом:
, 
(
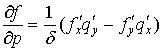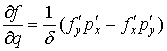
в области 
).
Для
системы дифференциальных уравнений в формальных производных (1) решается
следующая краевая задача.
Найти решение
системы (1) в окрестности точки 
, удовлетворяющее условиям:
, 
,
где 
– произвольные
аналитические функции от 
в рассматриваемой
области 
, 
– произвольная
фиксированная точка области 
; 
–
F-производная функции 
по функции 
[2].
В дальнейшем будем предполагать, что все
искомые и известные функции являются аналитическими от функций 
и 
в области 
. Следовательно, они будут и аналитическими от дуальных
функций 
, 
, что, конечно, не требует обязательной аналитичности всех
указанных функций от переменных 
. В алгебре дуальных чисел класс всех аналитических от 
и 
в области 
функций обозначим
через 
.
Далее
заметим, что можем, не уменьшая, по существу, общность исследования, допустить
разложение любой рассматриваемой нами функции 
класса 
во всей области 
в ряд вида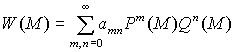 
(
;
– произвольная точка односвязной области 
плоскости 
), причем предполагаем существование таких постоянных 
, 
, что
в области 
; 
,
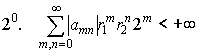а потому в области 
сходится абсолютно и
равномерно ряд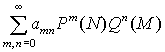 
(ведь 
).
Дуальную
функцию 
будем называть
моногенной по дуальной функции 
( в смысле
В.С. Федорова) [2] в области 
, если найдется такая дуальная функция переменных 
, которую обозначим 
, что имеем в указанной области:
, 
.
Вводим
дифференциальный оператор
.
Из
определения оператора 
непосредственно
вытекает, что система (1) равносильна уравнению
,
(2)
где 
; 
; 
; 
.
Таким
образом, поставленная краевая задача редуцируется к аналогичной задаче для
уравнения (2).
Требуется
найти решение дифференциального уравнения в формальных производных (2),
удовлетворяющее условиям:
,
где 
– заданная дуальная
функция, моногенная в смысле В.С. Федорова по функции 
в области 
.
Используя
результаты работы [3], решение краевой
задачи для уравнения (2) приводится к решению интегрального уравнения
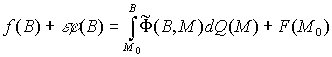, (3)
где интеграл берется по
кусочно-гладкой кривой, соединяющей точки 
и 
в области 
, и не зависит от пути интегрирования,
,
,
.
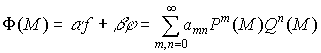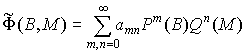Уравнение
(3), как показано в работе [3], решается
методом последовательных приближений. Найдя решение интегрального уравнения (3)
и выделив в этом решении 
и 
, мы найдем решение поставленной краевой задачи для системы
(1).
Литература:
1.
Стельмашук Н.Т. О
некоторых линейных дифференциальных системах в частных производных // Сибирский
математический журнал, 1964.– Т. 5, № 1.– С. 166-173.
2.
Федоров В.С. Основные свойства
обобщенных моногенных функций // Известия вузов. Математика, 1958.– № 6.– С.
257-265.
3.
Стельмашук Н.Т. Об одной
линейной системе в формальных производных // Anal. stiint. Univ. Iasi,
1962.–Т. 8, f. 2. – P. 331-342.