Фазовые потоки одного семейства кубических систем в круге Пуанкаре

Андреев А.Ф., Андреева И.А.

(Россия. Санкт-Петербургский государственный университет,

Санкт-Петербургский государственный политехнический университет)

Мы исследуем динамическую систему

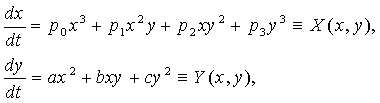(0.1)

где – параметры, формы и – взаимно просты, Не ограничивая общности, считаем, что

Как известно, траектории вещественной автономной полиномиальной системы, будучи соответствующим образом параметризованы, порождают на плоскости непрерывный поток (см., например, [5. С.23,24]). Из этого очевидно следует, что образы этих траекторий в круге Пуанкаре. Полученные суперпозицией отображений плоскости на нижнюю полусферу Пуанкаре и этой полусферы в открытый круг Пуанкаре порождают непрерывный поток в последнем. Будем для простоты называть образы траекторий системы (0.1) в ее траекториями в этом круге и говорить, что они продолжимы на все

Наше исследование состоит из частей I-IV. Части I-III – подготовитель-ные. Введенные в них понятия и обозначения и полученные в них результаты мы используем в части IV. Ссылки на них оформляем в виде: номер части, точка, номер объекта из нее. В частности, мы постоянно употребляем в них обозначения:

А результаты их таковы. В части I мы выявили все возможные топологические типы (Т-типы) конечной особой точки системы (0.1), в части II сделали то же для всех ее бесконечно удаленных особых точек (БО-точек) где а – вещественные корни полинома В этих частях мы указали и критерии всех возможных Т-типов особых точек в терминах числа, кратностей и последования на оси и корней многочленов и В части III для каждого случая системы (0.1), характеризующегося 1) фиксированной парой где – число вещественных корней полинома и 2) фиксированным порядком последования всех этих корней на оси u, мы описали Т-типы всех существующих у нее в этом случае особых точек.

Часть IV – основная. В ней мы для каждого случая системы (0.1). указанного в части III, ищем возможные для него фазовые портреты (ФП) системы в круге Пуанкаре . Их исследование составляет §§ 1-9 части IV. Но ее начало (§§ 0,1) опубликовано как часть IV [4]. Её нулевой параграф тоже подготовительный. В нём вводятся новые понятия (которые мы будем прилагать далее и к системе (0.1)), а именно: топодинамический тип (ТД-тип) особой точки системы, максимальная простая инвариантная для системы ячейка (МП-ячейка) круга Ω (просим читателя ознакомиться с этими понятиями непосредственно по статье IV₁, впрочем, из дальнейшего в основном всё будет ясно и без этого). Там же излагается единая программа исследования случаев 1-9 (которая далее, по существу, повторяется).

Для оформления ФП системы мы применяем не графическое его изображение (рисунок), а описательное, табличное, называя соответствующею таблицу описательным фазовым портретом (ОФП) системы. Это менее наглядно, но рационально, ибо в рассматриваемых нами случаях бόльшая часть ОФП системы может быть получена «малой кровью» - экономным методом деформации базовой таблицы (методом ДБТ [IV₁. Замечание 1.2]). Он применяется ниже в таблицах 1.1, 2.1, 3.1.

В настоящем сообщении мы излагаем ход исследований типовых случаев из §§ 1-3 части IV.

§ 1. . Система (0.1) имеет вид

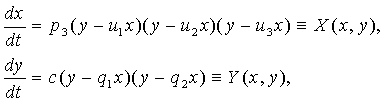(0.1)₁

где Её особыми точками в круге Пуанкаре являются: конечная точка БО-точки Для последования по возрастанию всех пяти чисел существует 10 различных случаев. Но среди них есть четыре пары случаев, взаимно обратных в смысле определения III.6.1 (т.е. переходящих друг в друга при замене в (0.1)₁ и изменении нумерации корней и полиномов P(u) и Q(u) на обратные). Мы рассматриваем лишь случаи, попарно независимые в этом смысле. Таковы, например, случаи 1.1-1.6, рассмотренные в IV₁. Проследим ход исследования одного из них.

Случай 1.1: < < < < . Реализуя программу IV₁.0.2, сначала ищем для случая 1.1 системы (0.1)₁ ТД-типы особых точек. Для точки O делаем это так. По таблице I.1.1 (строка 1) или III.6.1₁ (строка 1) находим Т-тип точки O для случая 1.1: слово где буква S означает седловой пучок O-кривых системы (он состоит из одной O-кривой), буква N – узловой (открытый пучок) O-кривых, S₀ (S⁰) – пучок, примыкающий к точке O по направлению x = 0, y < 0 (x = 0, y > 0). S₁ , N₁ (S₂, N₂) – пучки, примыкающие к O по направлениям прямой в слове А_O они перечисляются в круговом порядке следования при обходе точки O в (+)-направлении. Далее, учитывая, что [I. Случай 1.1] есть -кривая системы (т.е. примыкает к O при из полуплоскости x > 0), а поле направлений системы непрерывно, заключаем: ТД-тип особой точки O системы (0.1)₁ описывает слово

(1.1.0)

В нём для каждого из пучков O-кривых S, N верхний индекс означает, что этот пучок состоит из -кривых, а нижний индекс каждого из пучков S означает, что он представляет собою -кривую. Пучок не имеет нижнего знакового индекса.

Для БО-кривых в случае 1.1 ТД-тип находим так. По таблице III.6.1₂ находим их Т-типы: слова Апелляция к системе II.(2.1), для которой точки O_i , являются конечными особыми точками [II. Определение 2.1], позволяет найти верхние и нижние знаковые индексы пучков S, N O_i –кривых, образующих эти слова. Результаты этой работы составляют содержание таблицы 1.1.0.

Таблица 1.1.0. ТД-типы БО-точек в случае 1.1

Подслучай (пс)
1	0 < u1
2	u1 = 0	(Ø)	–	-”-	-”-
3	u1 < 0 < u2			-”-	-”-
4	u2 = 0	Ø	-”-	–	-”-
5	u2 < 0 < u3		-”-		-”-
6	u3 = 0	(Ø)	-”-	-”-	–
7	u3 < 0		-”-	-”-

В ней в словах верхний индекс пучка N или S означает,

что образующие его O_i -кривые примыкают к точке O при , а

его нижний индекс означает, что этот пучок примыкает к O_i из области

u > u_i (u < u_i).

Далее, действуя по программе IV₁.0.2, для каждого из указанных в таблице 1.1.0 подслучаев 1-7 случая 1.1, делаем следующие шаги.

1) Составляем перечень сепаратрис особых точек системы, т.е. примы-кающих к ним пучков типа S O- или O_i -кривых. (Будем иногда называть их сепаратрисами системы.) Согласно слову (1.1.0) и таблице 1.1.0 для каждого из пс 1,3,5,7 этот перечень имеет вид

(1.1.1)

А в каждом из пс 2,4,6 одна из этих сепаратрис отсутствует: в пс 2 – в пс 4 – в пс 6 – Но, как мы увидим далее, в любом из пс могут существовать значения параметров системы, при которых какие-либо две из указанных сепаратрис совпадают.

2) Рисуем БД-карту системы, а именно: в круге Пуанкаре строим поле направлений системы. Отмечаем её особые точки и возле каждой из них изображаем графически всю ту информацию, которую даёт для неё слово (1.1.0) или таблица 1.1.0. Пучок S изображаем одной направленной дугой, расположение и направление которой соответствуют его знаковым индексам, а пучок N – двумя-тремя такими дугами.

3) По БД-карте изучаем глобальное (при всех ) поведение каждой из имеющихся у системы в данном пс сепаратрис, руководствуясь при этом правилом, которое (в автодорожных терминах) формулируется следующим образом. Начав движение от какой-либо особой точки по её -сепаратрисе и попав (по выходе из малой окрестности этой точки) на «бездорожье», где «дороги» (сепаратрисы системы) нам и предстоит прочертить, двигаемся, воспринимая указатели направления поля системы как предписывающие знаки «разрешенных парковок». Траектория такого движения от точки до точки «парковки» и есть возможное максимальное продолжение исходной сепаратрисы. Если все сепаратрисы ведут себя однозначно: каждая из них имеет фиксированную (для данного пс) пару предельных точек, то они осуществляют вполне определённое разбиение круга на МП-ячейки (число которых равно числу сепаратрис), т.е. система имеет (в данном пс) один определённый ФП; таблице, дающей его ОФП, мы присваиваем номер 1.1.k, – номер пс. В противном случае для данного пс получается несколько вариантов ФП.

Проделав эту работу для всех семи подслучаев случая 1.1, мы пришли к следующим выводам.

Подслучай 1: Все сепаратрисы (1.1.1) ведут себя однозначно система имеет один определённый ФП. ОФП системы даёт таблица 1.1.1.

Подслучай 3: Три сепаратрисы из списка (1.1.1) ведут себя однозначно и при продолжении на все t ведут себя неоднозначно: они по одному разу пересекают полуось y = 0, x < 0, при значениях x, скажем и соответственно, где а для возможны варианты 1) 2) 3) 4) 5) пс 3 распадается на подподслучаи (ппс) для каждого из которых справедлив вывод, сделанный для пс 1. ОФП для них дают таблицы

Подслучай 5: Справедливо всё, сказанное для пс 3. ОФП системы дают таблицы 1.1.5_l ,

Подслучай 7: Справедливо сказанное для пс 3 с тем лишь отличием, что в пс 7 а для возможны варианты: 1) 2) 3) 4) 5) пс 7 распадается на ппс в каждом из которых система имеет один ФП. ОФП для этих ппс дают таблицы 1.1.7_l ,

Подслучай 2: Сепаратриса отсутствует. Остальные пять ведут себя однозначно и разбивают круг Ω на пять МП-ячеек. ОФП системы даёт таблица 1.1.2.

Подслучай 4: Сепаратриса отсутствует. Для , и справедливо то же, что и в пс 3 пс 4 распадается на ппс 4_l , ОФП для них дают таблицы 1.1.4_l ,

Подслучай 6: Сепаратриса отсутствует. Для и справедливо то же, что и в пс 3, т.е. (в тех же обозначениях) возможны варианты: 1) 2) 3) пс 6 распадается на ппс 6_l , Таким образом. Для системы (0.1)₁ в случае 1.1 возможны 25 различных ФП. Их описанные варианты (таблицы 1.1.1, 1.1.3_3,5 и 1.1.7_1,3,5) мы выписываем явно. Остальные 19 нам даёт метод ДБТ по рецептам таблицы 1.1.

Таблица 1.1.1. ОФП для пс 1

			Источник Сток

Таблица 1.1.3₃ . ОФП для ппс 3₃

Строки 1,2,3 как в таблице 1.1.1 с заменами в строках 1,2:

В таблице 1.1.1 ‒ МП-ячейка круга Ω, ‒ её граница, далее ‒ источник сток для потока . Граничные сепаратрисы ячейки выписываются в порядке их следования при обходе ячейки по её границе в -направлении; участки границы, лежащие на границе круга , опускаются. «Шапка» каждой такой таблицы далее также опускается, ибо она стандартна.

Таблица 1.1.3₅ . ОФП для ппс 3₅

Строки 1,2,6	См. таблицу 1.1.33

Таблица 1.1.7₁ . ОФП для ппс 7₁

Строки 1,2,6	См. таблицу 1.1.73

Таблица 1.1.7₃. ОФП для ппс 7₃

Таблица 1.1.7₅. ОФП для ппс 7₅

Строки 1,2,3 те же, что и в таблице 1.1.73

Таблица 1.1. ОФП для 19 пс и ппс случая 1.1

Искомая таблица	Базовая таблица	Деформация базовой таблицы	Перенуме-рация строк
1.1.2	1.1.1, 1.1.31	Удаление стр.6 и из стр.5	–
1.1.31	1.1.1	Замены в стр. 1,2,4: , замена стр.6 на	–
1.1.32	1.1.31,3	Удаление строки 5
1.1.34	1.1.33,5	-“- 4
1.1.4l ,		-“- 2
		Замена стр.2 на , замены в стр.5,6:	–
	,	Удаление стр. 6 и из стр. 5	–
	1.1.71,3	Удаление стр .4
	1.1.73.5	-“- 5

§ 2. . Система (0.1) имеет вид

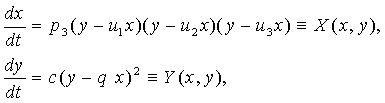(0.1)₂

где Она имеет в круге те же особые точки, что и система (0.1)₁. Для расположения числа q относительно чисел возможны случаи: 1) 2) 3) 4) Но случаи 4 и 3 взаимно обратны в смысле определения III.6.1 случаям 1 и 2 соответственно. Поэтому их мы опускаем. Но и из случаев 1 и 2 мы здесь ограничимся рассмотрением первого.

Случай 2.1: < < < . Для него Т-типы особых точек даёт таблица III.6.2, строка 1, а учет того, что для (0.1)₂ при позволяет получить их ТД-типы (см. таблицу 2.1.0).

Таблица 2.1.0. ТД-типы особых точек в случае 2.1

Подслучай
1. 0 < u1
2. u1 = 0	“	(Ø)	–	“
3. u1 < 0 < u2	“			“
4. u2 = 0	“	Ø	“	–
5. u2 < 0 < u3	“		“
6. u3 = 0	“	(Ø)	“	“
7. u3 < 0	“		“	“
8. q = 0			“	“	“
9. q <0		“	“	“	“

Как следует из таблицы 2.1.0, особые точки системы (0.1)₂ имеют следующие сепаратрисы. Точка О: в подслучаях (пс) 1-7 S₀, S₊, S⁰, в пс 8 S₀, S₊ , S _- , в пс 9 S₀, S⁰, S_-. БО-точки: в пс 1,3,5,7-9 S₁^-_, S₂⁺, S₃^-, в пс 2 S₂⁺, S₃^-, в пс 4 S₁^-, S₃^-, в пс 6 S₁^-, S₂⁺. Метод БД-карты показывает, что в каждом случае из пс 1,2,6-9 глобальное взаимное расположение веса сепаратрис неизменно, а в каждом из пс 3-5 S₁^- и S₃^- по одному разу пересекают полуось y = 0, x < 0, скажем, в точках x₁ и x₃, но для последующих имеют место возможности: 1) x₁ < x₃ , 2) x₁ = x₃ , 3) x₃ < x₁. Таким образом, в пс k возникают ппс . Следовательно, каждому из пс и каждому из ппс , , соответствует определённый ФП системы (0.1)₂. Его описательный вариант (ОФП) дает соответственно таблица 2.1.k или 2.1.k_l . Таким образом, для системы (0.1)₂ в случае 2.1 возможны 15 различных ОФП, четыре из них мы выписываем явно. Остальные 11 нам дает метод ДБТ (таблица 2.1).

Таблица 2.1.1. ОФП для пс 1

Таблица 2.1.3₃. ОФП для ппс 3₃

Таблица 2.1.7. ОФП для пс 7

Таблица 2.1.8. ОФП для пс 8

Отметим: в таблице 2.1.3₃ строки 1,2,3 совпадают с таковыми из таблицы 2.1.1 с точностью до замен а в таблице 2.1.8 строки 1,2 те же, что и в таблице 2.1.7.

Таблица 2.1. ОФП для 11 пс и ппс случая 2.1

Искомая таблица	Базовая таблица	Деформация базовой таблицы	Перенуме-рация строк
2.1.2	2.1.1	Удаление стр.6 и из стр.5	–
2.1.31	2.1.1	Замена стр.6 на	–
2.1.32	2.1.31,3	Удаление стр.5
2.1.4l ,	2.1.3l (5l)	Удаление стр.2 и из стр.1
2.1.51		Замена стр.2 на , замена стр.6 на	–
2.1.52	2.1.51	Удаление стр .4
2.1.54	2.1.33	Та же замена стр. 2, что и для 2.1.51. Замена стр. 6 на
2.1.6	2.1.53, 2.1.7	Удаление стр.6 и из стр.5	–
2.1.9	2.1.8	Замена в строках 1,3 на	–

§ 3. (m, n)=(3,0). Система (0.1) имеет вид

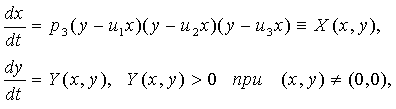(0.1)₃

где . Она имеет в круге те же особые точки, что и системы (0.1)₁ и (0.1)₂. Для нее мы имеем один случай: << но различаем подслучаи: 1) 2) 3) … , 7) Из таблицы III.6.3 и 2-го уравнения системы следует, что для любого из подслучаев 1-7 ТД-тип ее особой точки O а ТД-типы БО-точек таковы же, что и в таблице 2.1.0. На базе этой информации нетрудно заключить, что для системы (0.1)₃ возможны 13 различных ФП (по одному для каждого из пс 1,2,6,7 и по три для каждого из пс 3,4,5). ОФП для них дают таблицы 3.1.k, и а все эти таблицы дает метод ДБТ (таблица 3.1).

Таблица 3.1. ОФП системы (0.1)₃

Искомая таблица	Базовая таблица	Деформация базовой таблицы	Перенуме-рация строк
3.1.k, k=1,2,6,7	2.1.k	Удаление стр. 3, замена в стр.1 на
		-“-	-”-

Литература

1. Андреев А.Ф., Андреева И.А. Фазовые потоки одного семейства кубических систем в круге Пуанкаре. I. // Дифференциальные уравнения и процессы управления. Электронный журнал. 2007, № 4. С.17-26.

2. Андреев А.Ф., Андреева И.А. Фазовые потоки одного семейства кубических систем в круге Пуанкаре. II. // Дифференциальные уравнения и процессы управления. Электронный журнал. 2008, № 1. С.1-13.

3. Андреев А.Ф., Андреева И.А. Фазовые потоки одного семейства кубических систем в круге Пуанкаре. III. // Дифференциальные уравнения и процессы управления. Электронный журнал. 2008, № 3. С.39-53.

4. Андреев А.Ф., Андреева И.А. Фазовые потоки одного семейства кубических систем в круге Пуанкаре. IV_1. // Дифференциальные уравнения и процессы управления. Электронный журнал. 2009, № 4. С.181-213.

5. Пилюгин С.Ю. Пространства динамических систем. М.-Ижевск: научно-издательский центр «Регулярная и хаотическая динамика». 2008. 272 с.

SUMMARY

Andreev A.F., Andreeva I.A. Phase Flows of One Family of Cubic Systems in a Poincare Circle. IV.

A real autonomous system of second order differential equations is considered, right parts of which are reciprocal forms of phase variables x, y : a cubic form X(x, y) in a first equation and a quadratic form Y(x,y) in a second one. Presupposedly X(0,1)Y(0,1) not equals to zero. A task is posed to find all possible for this system phase portraits in a Poincare circle and to determine their criteria, close to coefficiential ones.

An investigation contains four parts. Parts I – III are preparatory. Topological types of singular points of the system are clarified in these parts – of a finite singular point O(0,0) and of all infinite singular points (IS-points). A main part is Part IV, in which a global behavior of trajectories of the system on plane or (it’s equivalent) a behavior of images of these trajectories in an open Poincare circle Ω is studied.

Part IV contains 9 paragraphs accordingly to a number of different pairs (m, n), where m{3,2,1} (n{2,1,0}) – a number of real roots of a polynomial P(u):= X(1,u) (Q(u):= Y(1,u)). In the present report a process of investigation of typical particular cases for the system from paragraphs 1, 2, 3 is clarified.