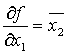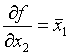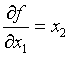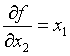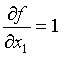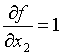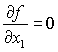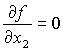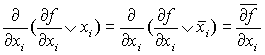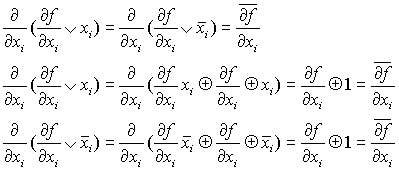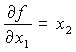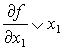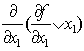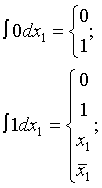Математика/2. Перспективы информационных систем

 

К.ф.-м.н. Лютикова Л.А.

Научно-исследовательский институт прикладной математики КБНЦ РАН, Россия

Исследование систем булевых функций логическими интегро-дифференциальными методами

 

Логическое дифференциальное и интегральное исчисления являются направлениями современной дискретной математики и находят свое применение в задачах динамического анализа и синтеза дискретных цифровых структур. Основным понятием логического дифференциального исчисления является производная булевой функции, представление о которой в виде булевой разности было получено  в работах [1,2].

Булева производная по некоторым своим свойствам является аналогом производной в классическом дифференциальном исчислении

Определение 1. Производная первого порядка  от булевой функции  f(x1,…xn)  по переменной xi есть сумма по модулю 2 соответствующих остаточных функций:

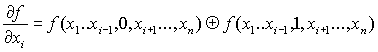                  (1)

 Определение   2 .Весом производной 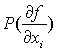 от булевой функции называется число конституент  («1») этой производной.

Утверждение 1 . Чем больше вес производной, тем больше функция f(x1,…,xn) зависит от переменной xi.

Определение 3. Смешанной производной k-го порядка от булевой функции f(x1,…xn)   называется выражение вида:

;

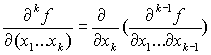При этом порядок фиксированной переменной не имеет значения. Производная k-го порядка определяет условия, при которых эта функция  изменяет свое значение при одновременном изменении значений x1…xk.
Определение 4.   Функция    f (x1,…,xn)   называется симметричной если             .
                                                                          Таблица 1

x1     x2

 f1           f2         f3        f4

 f1            f2            f5           f6

 0      0

 0       1       0         1

1

 0        1          0          1

1

 0      1

 1       0       0         1

0

 1        0          1          0

1

 1      0

 1       0       1         0

1

 1        0          0          1

0

 1      1

 1       0       0         1

0

 1        0          0          1

0

 
 

x1     x2

 f1           f2         f3        f4

 f1            f2            f5           f6

 0      0

 0      1       0        1

0

 0        1          0         1

0

 0      1

 0      1       1        0

1

 0        1          1         0

0

 1      0

 0      1       0        1

0

 0        1          0         1

1

 1      1

 1      0       0        1

1

 1        0          0         1

1

 
 

x1     x2

 f1           f2         f3        f4

 f1            f2            f5           f6

 0      0

0       1       0         1

  1

0         1          0         1

 1

 0      1

0       1       1         0

  1

1         0          1         0

 1

 1      0

1       0       1         0

  1

0         1          1         0

 1

 1      1

1       0       0         1

  1

1         0          0         1

 1

x1     x2

 f1           f2         f3        f4

 f1            f2            f5           f6

 0      0

 0      1       0        1

0

 0        1          0         1

0

 0      1

 0      1       1        0

0

 0        1          0         1

0

 1      0

 0      1       0        1

0

 0        1          1         0

0

 1      1

 0      1       1        0

0

 0        1          1         0

0

 
 
 
 
 
 
Свойство 1. Пусть булева функция от n переменных, ,  , тогда - существенные переменные.  Свойство 2. Для булевой функции   .
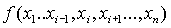
Свойство3. 
Доказательство: 


                                                                      Таблица 2

x1     x2

          f               

 0      0

      1      

0

0

1

 0      1

      1      

1

1

0

 1      0

      1      

0

1

1

 1      1

      0      

1

1

0

 
 

Если для булевой функции  f вычислена производная, то целесообразно рассмотреть одну из возможных конструкций неопределенного интеграла, отмечая особо, что природа логических функций обусловливает необходимость осторожного подхода к вопросу формирования конструкции интеграла булевой функции. При исследовании учитывались результаты практически единственной существующей в этой области работы [5], в которой интеграл булевой функции f от n переменных введен следующим образом:  .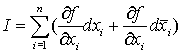

Введем следующее понятие интеграла:

Определение 5.  пусть 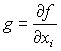 производная функции f по переменной xi , тогда существует функция , называемая булевым интегралом функции g, такая, что: , где h является произвольной булевой функцией переменных x1,…xi-1,xi+1,..,xn.

Свойство 3. Количество  L  первообразных  функции g= , где - булева функция,  равно  L=2n.
Теорема 1. Любая булева функция может быть получена в результате n-кратного логического интегрирования константы{0}.
 
 Доказательство:
Интегрируя каждую из полученных 4 функций по переменной x2 , получим все 16 булевых функций от двух переменных. Продолжая интегрирование по следующей переменной получим 256  функций Р2(3)=256 и т. д.
Минимизация ФАЛ                                
Совершенные нормальные дизъюнктивные формы хотя и дают однозначные представления функции, но являются очень громоздкими. Реализация СДНФ программно или схемотехнически является избыточной, что ведет к увеличению программного кода, поэтому существуют методы упрощения логической записи – минимизации.
 Определение 6. Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
При этом следует учесть, что ни один из способов минимизации не универсален.
Теорема 2. Пусть задана булева функция , тогда 
.
Пример:
Задана функция:
                                                                                   Таблица 3

x1         x2               x3

          f               

x1          x2              x3

          f               

 0          0            0

      1      

 1          0            0

     1

 0          0            1

      1      

 1          0            1

     0

 0          1            0

      0      

 1          1            0

     1

 0          1            1

      1       

 1          1            1

     1

 

СДНФ:

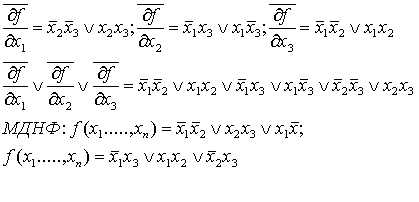
Литературы

1.       Reddy, S.M. Easily Testable Realizations for Logic Functions // IEEE Trans. Computers. Vol. 21, no. 11, Nov., 1982.

2.                 Горбатов В.А. Фундаментальные основы дискретной математика. Информационная математика. М: Наука, 2000.

3.                 Кузьмицкий Д.В., Шмерко В.П., Янушкевич С.И. Булево дифференциальное исчисление в вычислительной технике. Матричный аппарат булева дифференциального исчисления. Минск, 2007.

4.       Янушкевич С., Бохманн Д., Станкович Р., Тошич Ж., Шмерко В. Логическое дифференциальное исчисление: достижения, тенденции и приложения. // Автоматика и телемеханика. - 2004. - № 6. - С. 155-170.

5. Tucker, J.H. Tapia, M.A. Bennett, A.W. Boolean Integral Calculus for Digital Systems // IEEE Trans. On Comp., vol. 34, issue 1, Jan. 2000, p. 78-81.