Математика/5. Математическое моделирование

Бахтин Николай Иванович

аспирант кафедры «БЖДиООС» ЮРГТУ(НПИ), Россия

Метод моделирования движения газопылевого потока в обеспыливающих аппаратах.

Прогнозирование и анализ эффективности конструкции современных обеспыливающих аппаратов представляет собой очень важную задачу. Ключевым элементом решения этой задачи, на сегодняшний день, является применение современных компьютерных моделей, которые позволяют проанализировать характер работы аппарата без создания натурной модели. Эффективное использование вычислительной техники невозможно без создания современных математических моделей, описывающих рассматриваемый процесс.

Для моделирования работы обеспыливающих аппаратов очень важно построить модель движения дисперсной среды внутри аппарата, который может иметь довольно сложную геометрическую форму.

В работе предложена модель, позволяющая описать движение дисперсной среды с помощью функции распределения, предложен численный метод позволяющий осуществить необходимые расчеты.

Наиболее простым способом описания движения потока пыли является метод Монте-Карло [1]. Однако этот метод не позволяет работать с очень большим количеством частиц, так как время расчета увеличивается с ростом числа частиц. При очень большом количестве частиц метод Монте-Карло требует очень большого количества вычислительных ресурсов. Данное ограничение сдерживает применение метода для расчета движения мелкодисперсной пыли.

Использование функции распределения позволяет обойти указанное ограничение. Функция распределения характеризует распределение числа частиц в пространстве по скоростям их движения. Указанное понятие широко используется в механике воздушных сред [2], где в качестве частиц выступают молекулы воздуха. Использование функции распределения в аэродинамических расчетах позволяет заменить такие классические параметры как давление, скорость движения среды, плотность и д. р. Функция распределения является универсальным инструментом, она позволяет описать не только большое количество неупорядоченно движущихся молекул, но и дисперсную среду.

В аэродинамических расчетах функция распределения используется, как правило, в контексте кинетического уравнения Больцмана[2]:

(1)

где:

– скорость движения частицы,

– функция распределения,

– интеграл столкновений.

Соответственно, все методы расчета, использующие , по сути, являются численным методом решения дифференциального уравнения (1).

В данной работе используется оригинальный метод, не использующий кинетического уравнения Больцмана, а основанный на физической модели рассматриваемого процесса. Помимо этого, оригинальной является сама идея использования понятия функции распределения для описания движения дисперсной среды.

Предложенный метод, как и любой другой численный метод, предполагает разбиение области моделируемого пространства на конечное количество ячеек с конечным набором параметров. При работе с функцией распределения аналогичным образом разбивается и пространство скоростей. Каждая ячейка, полученная при дискретизации геометрического пространства и пространства скоростей, будет характеризоваться величиной:

, (2)

где:

– число частиц, заключенных в объеме ячейки ,

– объем ячейки в геометрическом пространстве,

– объем ячейки в пространстве скоростей,

– элементарный объем в геометрическом пространстве, элементарный объем в пространстве скоростей.

В итоге состояние системы описывается большим многомерным массивом. Для двухмерного случая это будет четырехмерный массив , где – индексы массива. Так как каждая ячейка, полученная при дискретизации, мала, то будем считать, что частицы распределены внутри этой ячейки в геометрическом пространстве равномерно, и имеют скорость, равную скорости средней точки объема в пространстве скоростей.

Так как при дискретизации образовалось множество «выборок» молекул по скоростям для каждой точки пространства, и мы считаем, что в каждой выборке все частицы движутся с определенной скоростью, то мы можем предсказать положение этих частиц через время . Если бы на частицы не действовала никакая сила, то они бы двигались по прямой. И весь ансамбль частиц заданной «выборки» после перемещения сохранил бы свою форму (рис. 1)

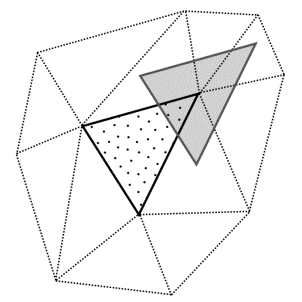
Рис. 1 Пример смещения ансамбля частиц.

После перемещения, частицы ансамбля попадут в другие ячейки геометрического пространства. При предположении, что частицы распределены равномерно и имеют одну и туже начальную скорость из рис. 1 видно, что независимо от количества частиц в ансамбле, пропорции между количеством частиц попавших в разные ячейки сохраняются. Следовательно, можно вычислить эти пропорции в предварительной фазе расчетов и потом использовать их в виде некоторых постоянных коэффициентов. Вынос наиболее трудоемких операций за пределы основного цикла расчета позволяет существенно сократить общий объем вычислений.

В случае, если частицы находятся в стационарном поле некоторых сил, характер движения этих частиц станет более сложным, но правило сохранения пропорций останется в силе.

Необходимо вычислить полный набор коэффициентов пропорций переноса в другие ячейки для каждой скорости из дискретного набора пространства скоростей. После этого, в основном цикле расчета, достаточно умножить число частиц ансамбля на коэффициент, что бы получить количество частиц, которые попадут в ту ячейку, для которой был определен заданный коэффициент.

Полная совокупность коэффициентов образует собой таблицу пропорций переноса из заданной ячейки частиц с заданной скоростью в другие ячейки. Использование данной таблицы в основном цикле расчета представляет собой простую последовательность умножений и сложений. По этой причине, несмотря на огромный размер таблицы, современные процессоры способны эффективно производить вычисления по таким алгоритмам.

Следует обратить внимание на то, что данный метод предполагает, что частицы дисперсной среды не взаимодействуют друг с другом, а имеет место только механическое перемещение частиц в потоке воздуха.

Решить подобную задачу с применением функции распределения можно было бы в рамках численного решения кинетического уравнения Больцмана. Однако такой подход имеет недостатки. Шаг по времени ограничен числом Куранта и большими трудностями при работе с ячейками неквадратной формы. Предложенный метод не имеет подобных ограничений и позволяет свободно выбирать шаг по времени и форму ячеек.

Довольно простая физическая модель, на которую опирается метод, делает работу интуитивно понятной и безопасной, т. е. можно осуществлять модификации более четко понимая, какие ограничения накладывают те или иные введенные допущения. При работе с разностными схемами решения дифференциальных уравнений не всегда очевидна сходимость или несходимость решения.

Предложенный в работе метод ориентирован на моделирование высокодисперсного газопылевого потока. Он может быть полезен там, где использование метода Монте-Карло затруднено в связи с большими вычислительными затратами при моделировании потоков с огромным количеством частиц.

Литература:

1. С. М. Ермаков. Метод Монте-Карло и смежные вопросы. – Главная редакция физико-математической литературы изд-ва «Наука», 1975г.

2. Черчиньяни К. Теория и приложения уравнения Больцмана. М.: Мир, 1978.

3. Численное решение многомерных задач газовой динамики. / Под редакцией С. К. Годунова. М.: Наука . 1976г.