К.т.н. Федосеев В.М.

Пензенская государственная технологическая академия, Россия

Способ аппроксимации логарифмической функции

Многочленные аппроксимации логарифмической функции имеют существенные недостатки. Не лишены их и другие виды аппроксимаций. В работе рассматривается подход к аппроксимации логарифмической функции, отличающийся по своим свойствам от известных способов и благодаря этому компенсирующий присущие им недостатки. Он особенно удобен при работе с логарифмическими моделями в задачах динамики, когда требуется в широком диапазоне определять значения логарифмов больших чисел.

Из математического анализа известно предельное равенство:

,

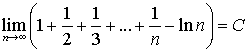в котором предел С (постоянная Эйлера) имеет значение С = 0,57721566490…. Отсюда следует, что для логарифмов натуральных чисел имеет место асимптотическая формула:

(1)

или её улучшенный вариант (находится из формулы Эйлера-Маклорена):

. (2)

Для наших целей формула (1) видоизменяется следующим образом:

. (3)

Для формулы (2) отклонение частей асимптотически оценивается величиной . Можно доказать, что в случае формулы (3) аналогичная оценка имеет значение .

Для того чтобы получить выражение, аппроксимирующее логарифмическую функцию при действительных значениях аргумента, запишем уравнение касательной прямой к графику функции в точке , воспользовавшись для значения логарифма формулой (3) при обозначении (целая часть числа ), и в итоге получим:

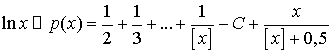. (4)

Если же для составления аппроксимирующей функции воспользоваться дробно-линейной интерполяцией на узлах: , при условии вычисления соответствующих значений логарифма по формулам (2) и (3), то получим другую формулу:

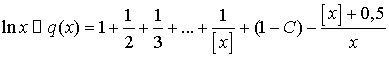. (5)

Как это будет видно из дальнейшего содержания, формула (5) по сравнению с формулой (4) обладает рядом преимущеcтв. На рис. 1 и 2 показаны графики аппроксимирующих функций из формул (4) и (5), иллюстрирующие поведение функций и на отрезке .

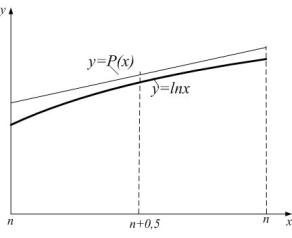
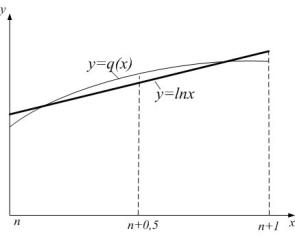
Рис. 1. Рис. 2.

Чтобы убедиться в эффективности формул (4) и (5) вычислим натуральный логарифм полного угла . В этом случае имеем: , , и после подстановки соответственно найдём:

,

.

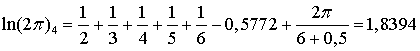Так как искомое число равно , то отклонение найденных значений логарифма от истинного составило: в случае использования формулы (4) - , формулы (5) - .

Общие оценки точности формул (4) и (5) следуют из теоремы:

Максимальное значение отклонения на отрезке имеет место при и составляет ; для функции при тех же условиях величина отклонения оценивается неравенством .

Доказательство теоремы основано на приведённых выше оценках для формул (2) и (3).

Свойства аппроксимации :

1) графиком функции является кусочная кривая, состоящая из ветвей, заданных на отрезках , ;

2) функция непрерывна (в точках стыка составных частей их значения совпадают);

3) при достаточно больших значениях отклонение функции от логарифма становится сколь угодно малым, при этом имеет место оценка ;

4) совпадение производных логарифма и аппроксимирующей функции происходит при х= [x]+0,5, в остальных точках отклонение производных имеет величину порядка 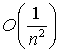; на такую же величину расходятся значения производных составных частей в точках стыка.

Таким образом, предлагаемый вид аппроксимации представляет собой конструкцию сплайнового типа, но в отличие от полиномиального сплайна в данном случае мы имеем общее аналитическое выражение для всех ветвей сплайна, и при этом оно распространяется на интервалы бесконечной длины.