УДК
539.3
Расчет плосконагруженных тонкостенных конструкций
с учетом геометрической нелинейности на основе
смешанного МКЭ
К.т.н.
Гуреева Н.А., д.т.н. Клочков Ю.В.,
д.т.н. Николаев А.П.
Волгоградская
государственная сельскохозяйственная академия, Россия
Для расчета
тонкостенных конструкций реализуется шаговый метод. Изложен алгоритм формирования матрицы деформирования четырехугольного
конечного элемента, узловыми неизвестными которого приняты приращения
перемещений и приращения деформаций.
Для численной реализации алгоритма получен смешанный
функционал на основе равенства возможной и действительной работ внешних и
внутренних сил на шаге нагружения.
Ключевые слова: метод
конечных элементов, смешанная формулировка, смешанный метод, билинейная
аппроксимация.
На
шаге нагружения плосконагруженной тонкостенной оболочечной конструкции разработан конечный элемент в виде произвольного
четырехугольника с узловыми неизвестными в виде приращений перемещений и
приращений деформаций.
Для формирования
матрицы деформирования конечного
элемента в геометрически нелинейной постановке получен функционал на основе
равенства возможной и действительной работ внешних и внутренних сил.
1. Геометрия
оболочки. Внутренняя поверхность
тонкостенной оболочки, рассматриваемой в
декартовой системе координат xOz, принимается в качестве отсчетной. Положение
произвольной точки М0 отсчетной
линии s определяется
радиусом-вектором
![]() , (1)
, (1)
где ![]() - орты декартовой
системы координат.
- орты декартовой
системы координат.
Векторы локального базиса точки М0 имеют вид
![]()
![]() . (2)
. (2)
Производные векторов локального базиса,
определяются дифференцированием (2) и представляются разложением по векторам
этого же базиса в матричном виде [1]
![]() ,
(3)
,
(3)
где ![]() ;
; ![]() .
.
Положение
точки ![]() , отстоящей на
расстоянии t от точки
, отстоящей на
расстоянии t от точки
![]() , определяется радиусом-вектором
, определяется радиусом-вектором
![]() .
(4)
.
(4)
Векторы
локального базиса точки ![]() имеют вид
имеют вид
![]() ;
;![]() . (5)
. (5)
2.
Перемещения и деформации. При реализации шагового нагружения произвольная точка
оболочки рассматривается в трех положениях: исходном М0t, деформированном после j шагов
нагружения Мt (вектор перемещения ![]() ) и соседнем - после (j+1)- го шага нагружения Мt* (вектор перемещения
) и соседнем - после (j+1)- го шага нагружения Мt* (вектор перемещения ![]() ).
).
Вектор перемещения ![]() представляется
компонентами в локальном базисе точки М0
выражением
представляется
компонентами в локальном базисе точки М0
выражением
![]() . (6)
. (6)
Производные вектора (6) с учетом (3) определяются соотношениями
![]() ;
; ![]() ,
(7)
,
(7)
где ![]() - функции компонент вектора
- функции компонент вектора ![]() и их производных.
и их производных.
Положение точки ![]() определяется радиусом-вектором
определяется радиусом-вектором
![]() (8)
(8)
Векторы
локального базиса точки Мt имеют вид
![]() ;
;
![]() . (9)
. (9)
При переходе из Мt в положение Мt*
точка получает перемещение, определяемое вектором в локальном базисе точки М0
![]() .
(10)
.
(10)
Производные
вектора (10) имеют вид
![]() ;
;![]() , (11)
, (11)
где ![]() ,
,![]() - функции компонент вектора
- функции компонент вектора ![]() и их производных.
и их производных.
Положение
точки Мt* определяется радиусом-вектором
![]() (12)
(12)
Локальный
базис точки Мt*определяются векторами
![]() ;
; ![]() . (13)
. (13)
Выражения
приращений деформаций на (j+1)- ом шаге нагружения имеют вид [2]
![]() ;
;
![]() ;
;
![]() . (14)
. (14)
Линейная
и нелинейная части приращений деформаций ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() с учетом (13), (9) могут быть представлены в матричной форме
с учетом (13), (9) могут быть представлены в матричной форме
![]() ,
,![]() , (15)
, (15)
где ![]() ;
; ![]() ; [L] – матрица алгебраических
и дифференциальных операторов.
; [L] – матрица алгебраических
и дифференциальных операторов.
На
шаге нагружения выражениями нелинейной части приращений деформаций ввиду их
малости можно пренебречь.
3. Соотношения между деформациями и
напряжениями. Связь между компонентами
тензора деформаций ![]() и компонентами
тензора напряжений
и компонентами
тензора напряжений ![]() выражается законом
Гука [2]
выражается законом
Гука [2]
![]() , (16)
, (16)
где ![]() - модуль упругости;
- модуль упругости; ![]() - коэффициент Пуассона.
- коэффициент Пуассона.
В
случае плоского напряженного состояния выражения (16) примут вид
![]() ;
;
![]() ; (17)
; (17)
![]()
![]() .
.
Соотношения (17) можно представить в матричной форме
![]() ;
;![]() , (18)
, (18)
где ![]()
![]()
На (j+1) – ом шаге нагружения зависимости между компонентами
тензора приращения деформаций и компонентами тензора приращений напряжений записываются
аналогично (18)
![]() , (19)
, (19)
где ![]()
![]() ;
; ![]() – матрица податливости материала.
– матрица податливости материала.
4. Матрица деформирования конечного
элемента на шаге нагружения. Разработан
конечный элемент в виде произвольного четырехугольника с узлами i, j, k, l, узловыми неизвестными которого принимяты приращения
перемещений и приращения деформаций. Для выполнения численного интегрирования произвольный
четырехугольник отображается на квадрат с локальными координатами ξ, η, изменение которых определяется неравенствами ![]() . Глобальные координаты
. Глобальные координаты ![]() , t
четырехугольника аппроксимируются через узловые значения биилинейными соотношениями
, t
четырехугольника аппроксимируются через узловые значения биилинейными соотношениями
![]() ;
; ![]() , (20)
, (20)
где ![]() ;
;![]() ;
; ![]() - вектор-строка функций формы.
- вектор-строка функций формы.
Производные
глобальных координат в локальной системе ![]() ,ξ, ,
,ξ, , ![]() ,η, t,ξ,
t,η и производные локальных
координат в глобальной системе
,η, t,ξ,
t,η и производные локальных
координат в глобальной системе ![]() , ξ,t,
, ξ,t, ![]() , η,t
определяются дифференцированием (20).
, η,t
определяются дифференцированием (20).
Аппроксимацию
вектора перемещения внутренней точки конечного элемента через компоненты векторов
перемещений узловых точек можно также представить билинейными соотношениями [1]
![]() ;
;![]() , (21)
, (21)
где ![]() ;
; ![]() .
.
Соотношения (21) можно представить в матричном виде
![]() , (22)
, (22)
где ![]() .
.
Производные
компонент (21) определяются выражениями
![]() ;
;![]() ;
;
![]() ;
;![]() . (23)
. (23)
С
использованием (15), (22), (23) линейные части приращения деформаций на шаге
нагружения представляются в матричном виде
![]() . (24)
. (24)
Компоненты тензора приращений
деформаций внутренней точки конечного элемента аппроксимируются через
компоненты тензора приращений деформаций узловых точек также билинейными
соотношениями, которые можно представить в матричном виде
![]() , (25)
, (25)
где ![]() ;
;
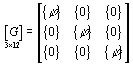 .
.
При
реализации шаговой процедуры нагружения функционал Лагранжа, выражающий
равенство возможных и действительных работ внешних и внутренних сил на шаге
нагружения, имеет вид
![]() (26)
(26)
где V –объем
деформируемого тела;S – площадь поверхности с заданной
внешней нагрузкой;![]() ;
;![]() - векторы нагрузок после j-го и (j+1)-го шагов соответственно.
- векторы нагрузок после j-го и (j+1)-го шагов соответственно.
Заменим выражение действительной работы внутренних сил в (26) разностью
их возможной и дополнительной работ
![]() (27)
(27)
С учетом (27) функционал (26) примет вид
![]()
![]() (28)
(28)
Функционал (28) с учетом (25), (22) и
(19) для отдельного конечного элемента на шаге нагружения принимает вид
![]()
![]() (29)
(29)
Минимизируя функционал (29) по узловым
неизвестным ![]() и
и ![]() , получим систему
уравнений
, получим систему
уравнений
![]() ;
;![]() , (30)
, (30)
где ![]() ;
; ![]() ;
; ![]() .
.
Систему (30) можно представить в
традиционной конечно-элементной форме
![]() ,
(31)
,
(31)
где 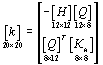 - матрица
деформирования конечного элемента;
- матрица
деформирования конечного элемента; ![]() - вектор узловых
неизвестных конечного элемента;
- вектор узловых
неизвестных конечного элемента; ![]() - вектор узловых
усилий конечного элемента на шаге нагружения.
- вектор узловых
усилий конечного элемента на шаге нагружения.
Для формирования матрицы деформирования
всей конструкции используется традиционная процедура МКЭ [3].
Список литературы:
1.Гуреева
Н.А. Решение плоской задачи теории упругости с использованием варианта МКЭ в
смешанной формулировке. Изв.вузов. Авиационная техника. Казань.2009.№2.с.8-11.
2. Седов Л.И. Механика сплошной среды, т.1. М.: Наука,
1976. 536 с.
3. Постнов В.А., Хархурим И.Я. Метод конечных
элементов в расчетах судовых конструкций. Л.: Судостроение, 1974. 344с.