Экономические науки/Математические методы в экономике

К.э.н. Андриенко В.М.

Одесский национальный политехнический университет

Фрактальные характеристики временных рядов фондовых индексов в предкризисный период

На основе традиционных аналитических методов анализа финансовых рынков оказалось невозможным предсказать мировые финансовые кризисы 1990-х – 2000-х гг. В связи с этим, приобрели актуальнсть исследования, посвященные выявлению показателей – предвестников, которые могут заблаговременно предупредить о наступлении негативной ситуации.

Существуют различные точки зрения на эту проблему. В работе [1] предложена система индикаторов – предвестников нестабильности на финансовом рынке России, разработанная на основе методологии «сигнального» подхода [2]. Под сигналом понимается выход того или иного индикатора за пределы порогового значения.

В рамках концепции эффективного рынка рассматривают волатильность рынков [3] и факторы, влияющие на волатильность. Предполагается, что количественные оценки факторов могут служить индикаторами негативных ситуаций на рынках. Этому направлению посвящены работы [3,4,5]. При этом используются классические эконометрические регрессионные методы анализа и моделирования. В [4] использовалась эконометрическая модель бинарного выбора, а в [5] проведено исследование на основе регрессионно - факторного анализа. Поскольку ситуация на рынке быстро меняется, то такого типа модели не могут использоваться на длительном временном горизонте. Для того, чтобы модель адекватно соответствовала ситуации, ее нужно строить заново.

В своей книге [6] Э.Петерс показал, что фондовые рынки обладают фрактальными свойствами и сформулировал гипотезу фрактального рынка. В рамках этой концепции исследуются динамические и структурные характеристики рынков на основе синергетики и эконофизики [7,8,9]. Для этого используется аппарат теории случайных матриц, мультифрактального, вейвлет-анализа, методы анализа рекуррентных диаграмм, энтропийные методы и тому подобное. Так, например, в [7] показано, что мультифрактальный спектр финансовых рядов данных проявляет специфическое поведение при кризисных обвалах. Накануне кризиса он сужается и экстремум смещается к нулю. В статье [8] на основе рекуррентного анализа, на примере котировок фондового индекса S&P500 сделан вывод о том, что наиболее информативной мерой для мониторинга рынка является ламинарность исследуемых данных. Однако, вопросы универсальности приведенных показателей требуют обсуждения.

Данная работа направлена на исследование фрактальных свойств временных рядов мировых фондовых индексов и выявление закономерностей в данных процессах в предкризисные периоды на основе R/S анализа. Основным показателем выступает фрактальная размерность, которую отражает показатель Херста [6].

В таблице 1 приведены значения показателя Херста для индексов разных стран по ежедневным значениям индекса на момент закрытия торгов за период 2000-2014гг. Из таблицы видно, что в предкризисный период, на всех рынках произошло снижение значений показателя Херста. Это наглядно отражают графики на рисунке 1.

Таблица 1

Значения показателя Херста

Год Страна	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013
Индия (Bse-sensex)	0,53	0,52	0,55	0,51	0,45	0,51	0,50	0,49	0,48	0,50	0,49	0,45	0,56	0,40
Франция (CAC)	0,41	0,54	0,46	0,46	0,37	0,48	0,46	0,48	0,48	0,51	0,41	0,45	0,47	0,47
Германия (DAX)	0,49	0,56	0,46	0,49	0,45	0,47	0,46	0,48	0,50	0,51	0,46	0,48	0,49	0,44
США(dow-Jones)	0,46	0,53	0,45	0,46	0,49	0,47	0,46	0,46	0,47	0,53	0,47	0,46	0,48	0,50
Гонконг (Hang-seng)	0,47	0,52	0,51	0,48	0,53	0,47	0,47	0,52	0,47	0,51	0,52	0,45	0,51	0,47
Бразилия (Ibovespa)	0,51	0,47	0,47	0,52	0,43	0,46	0,50	0,47	0,50	0,46	0,47	0,48	0,50	0,48
Россия (ММВБ)	0,53	0,54	0,47	0,51	0,52	0,50	0,51	0,54	0,50	0,45	0,45	0,46	0,54	0,44
Япония (Nikkei)	0,52	0,51	0,50	0,48	0,43	0,46	0,47	0,47	0,50	0,60	0,46	0,47	0,59	0,46

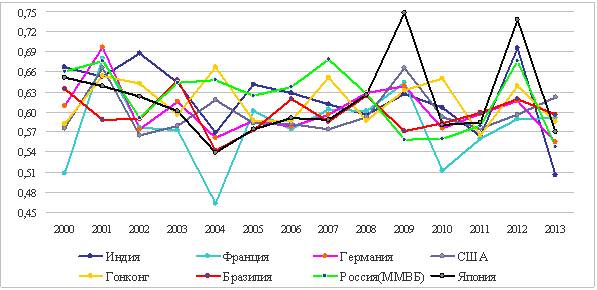
Рис.1. Динамика показателя Херста

Таким образом, можно предположить, что возникновение описанной ситуации может быть предвестником кризиса.

Классификация временных рядов по значениям показателя Херста производится следующим образом:

1) - означает антиперсистентность, то есть фондовый индекс меняет направление чаще, чем случайный ряд. Чем ближе значение к нулю, тем неустойчивей динамика индекса (за подъемом следует спад и наоборот).

2) - указывает на то, фондовый индекс обладает персистентным свойством. Он характеризуется эффектами долговременной памяти и имеет склонность следовать трендам. Если индекс возрастает (убывает) в предыдущий период, то вероятно, что он будет сохранять эту тенденцию какое-то время в будущем. Трендоустойчивость поведения увеличивается при приближении к единице.

3)  - соответствует случайному ряду. Данные случайны и независимы. Такой процесс полностью лишен памяти. Рынок стагнирует, нет никаких движений или они цикличны с очень большой частотой колебаний [6].

Оценки показателя для всех рынков находятся в интервале [0,37; 0,6 ]. В соответствии с R/S −анализом необходимо протестировать нулевую гипотезу о том, что исследуемый временной ряд значений фондового индекса является случайным. Для этого вычисляется статистика [7,10]. Нулевая гипотеза принимается на соответствующем уровне значимости, если статистика попадает в какой- либо из интервалов таблицы 2. В противном случае, можно считать, что с вероятностью ряд не является случайным [10].

Таблица 2

Область принятия гипотезы для статистики

Уровень значимости	0,005	0,025	0,05	0,1	0,2	0,3	0,4
Интервал принятия гипотезы	0,721 - 2,098	0,809 - 1,862	0,861 - 1,747	0,927 - 1,620	1,018 -1,473	1,090-1,374	1,157-1,294

В таблице 3 приведены значения статистики для индексов, приведенных в таблице 1.

Таблица 3

Значения статистики

Год Индекс	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009	2010	2011	2012	2013
Индия (Bseensex)	0,8870	0,8407	0,8975	0,8719	1,0486	0,8809	0,9525	0,8734	0,8699	0,8847	0,8776	1,1379	0,9757	1,1395
Франция (CAC)	1,1626	0,8935	0,9014	0,8998	1,0179	0,9211	0,9658	1,2234	0,8899	0,8785	1,2662	0,9462	1,0732	0,9419
Германия (DAX)	1,0103	0,9082	0,8825	0,8704	1,1840	0,9008	0,9455	0,9686	0,9138	0,8651	0,9032	1,0176	1,0194	0,8856
США (Dow-Jones)	0,8284	0,9727	0,9237	0,8643	1,3032	1,2814	0,9481	1,0014	0,8759	0,8682	0,9599	1,0966	0,9951	0,9439
Гонконг (Hang-seng)	1,0042	0,8393	0,9463	0,8636	1,0561	0,9666	0,9462	0,8736	0,8941	0,8600	0,9695	0,9215	0,9898	1,0845
Бразилия (Ibovespa)	0,9185	0,8443	0,9149	0,8662	0,9692	0,9572	0,9476	0,8449	0,8678	0,8313	1,1101	0,9092	1,0294	0,9598
Россия (ММВБ)	1,0054	0,9950	0,9167	0,8510	1,0550	0,8812	1,0403	1,0712	0,9034	0,8361	0,9489	0,9711	1,0075	1,1278
Япония (Nikkei)	0,8595	0,9167	0,8736	0,9015	1,2826	0,8968	1,1266	1,0572	0,9239	0,8856	1,0220	0,9876	1,1244	0,9453

Для значений , гипотеза о случайности ряда отклоняется на уровне значимости . Таким образом, вероятность того, что данные представляют случайный ряд, равна . С ростом эта вероятность увеличивается, а для некоторых индексов нулевая гипотеза принимается (например, для данных таблицы 3 за 2006-2007г.г.). По графикам рисунка 2 видно, что это происходит как раз в предкризисный период, когда . Это свидетельствует о том, что фондовые индексы в предкризисный период могут изменять свои свойства.

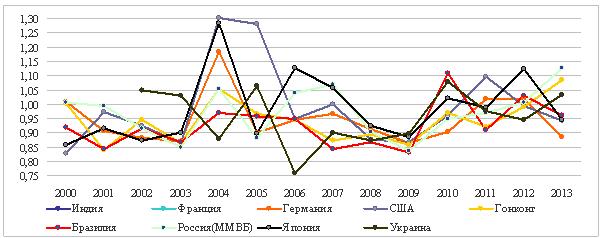
Рис. 2. Динамика статистики .

Фрактальная размерность связана с показателем Херста простым соотношением . Снижение влечет увеличение фрактальной размерности. На практике это означает, что возрастает число инверсий в эмпирических данных, то есть динамика рынков становится менее устойчивой и более непредсказуемой. На рисунке 3 приведены графики динамики американского индекса Dow −Jonеs в 2005-2008г.

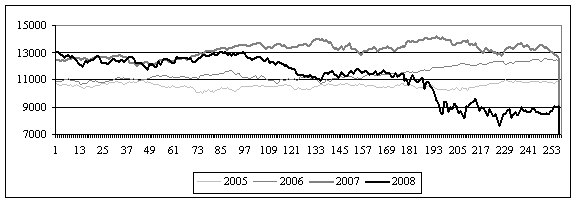
Рис.3. Динамика индекса Dow-Jonеs в 2005-2008гг.

Из рисунка видно, что в предкризисный период индекс демонстрировал поступательный рост, тем не менее, в 2008г. произошло резкое изменения тенденции. График 2005г. - это практически гладкая линия, а в период 2006-2007гг. график становится зазубренным, индекс меняют направление чаще. Индексы других стран демонстрируют аналогичную ситуацию. Таким образом, можно констатировать, что в предкризисный период увеличивается фрактальная размерность пространства эмпирических данных, изменяются их свойства. Это может быть предвестником дестабилизации рынка.

Литература:

1. Разработка опережающего индекса финансовой стабильности в РФ. Институт экономической политики им. Е. Т. Гайдара, группа «Открытие Капитал» [Електронний ресурс], М: 2011. — Режим доступа: www.otkritie.com.

2. Kaminsky G., Lizondo S., Reinhart C. Leading Indicators of Currency Crises // IMF Staff Papers. 1998. Vol. 45 (March). pp. 1-48.

3. Bloom N. The Impact of Uncertainty Shocks//Econometrica.-2009.-Vol.77.- №3.-С.623-685.

4. Федорова Е.А., Назарова Ю.Н. Финансовые индикаторы кризисной ситуации Российского фондового рынка [Текст] // Аудит и финансовый анализ. - 2009. - N 6. - С. 442-446.

5. Андриенко В. М. Оценка влияния макроэкономических показателей на динамику фондового индекса ПФТС [Електронний ресурс] /В. Андриенко // Соціально-економічні проблеми і держава. — 2013. — Вип. 1 (8). — С. 31–43. — Режим доступа: http//sepd.tntu.edu.ua/images/stories/pdf/2013/13avmfup.pdf.

6. Петерс Э. Фрактальный анализ финансовых рисков./Петерс Э. Интернет-трейдинг М.:2004. -304 с.

7. Дербенцев В.Д., Сердюк О.А., Соловйов В.М., Шарапов О.Д. Синергетичні та еконофізичні методи дослідження динамічних та стуктурних характеристик економічних систем// Монографія. Черкаси, 2010.

8. Соловьёва В.В., Тулякова А.Ш. Использование мультифракталов в анализе фондовых рынков //Монографія. Інформаційні технології та моделювання в економіці: на шляху до міждисциплінарності. Черкаси 2013– С. 130-140.

9. Піскун О.В. Особливості застосування рекурентних діаграм і рекурентного кількісного аналізу для дослідження фінансових часових рядів / О.В. Піскун // Фінансовий простір. – 2011. – № 3 (3). – С. 111 – 118.

10. Andrews D. Non-Strong Mixing Autoregressive Process//Journal of Probability.-1984.-№21.-P.- 930-934.999.