Математика / 5. Математическое моделирование

к.т.н. Крючин О.В.

Тамбовский государственный университет им. Г.Р. Державина, Россия

Перспективы применения параллельных вычислений к обучению искусственных нейронных сетей при помощи метода обратного распространения ошибки

Как известно, обучение искусственных нейронных сетей (ИНС) характеризуется рядом специфических ограничений, таких как большое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач и необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. Именно эти ограничения выделяют обучение ИНС из общих задач оптимизации, кроме того оно имеет ряд существенных недостатков, например, неопределённо долгий процесс обучения.

Для решения проблемы значительных временных затрат часто используются параллельные вычисления. В работах [1-2] описаны параллельные методы подбора структуры сети, весовых коэффициентов при помощи классических градиентных методов или вычисления невязки. Интерес вызывает также метод обратного распространения ошибки, который был разработан и усовершенствован рядом отечественных [3-4] и зарубежных [5-6] ученых. Основная идея состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Обучение ИНС можно представить как задачу оптимизации, для чего строится функция оценки, которая явно зависит от выходных сигналов сети и неявно от всех её параметров, например,

	(1)

где , — -ые выходные вектора моделируемого объекта и ИНС.

Для модификации весового коэффициента используется стохастический градиентный спуск, то есть значения весов изменяются после каждой строки обучающей выборки в сторону, противоположную градиенту

,	(2)

где — множитель, задающий скорость изменения, а — элемент вектора градиента 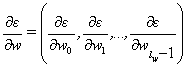. Поскольку на выход сети влияет только часть суммы , где сумма берется по входам -го узла, то справедливо утверждение .

Аналогично, влияет на общую ошибку только в рамках выхода -го узла , поэтому справедливо следующее утверждение

,	(3)

где , , — соответствующая сигмоида, в данном случае — экспоненциальная. Если обозначить , то можно сформулировать выражение

.	(4)

Если же -й узел не расположен на последнем уровне, то у него есть выходы и в этом случае , , — это в точности аналогичная поправка, но вычисленная для узла следующего уровня будем обозначать ее через — от она отличается отсутствием множителя . Поскольку можно вычислять поправку для узлов последнего уровня и выражать поправку для узла более низкого уровня через поправки более высокого, то, как показано в работе [8], для узла последнего уровня поправка вычисляется по формуле , для внутреннего узла сети и для всех узлов .

Поскольку метод обратного распространения ошибки, в отличии, от прочих не использует полного вычисления невязки (1), то параллелить этот алгоритм на уровне вычисления погрешности не представляется возможным. С другой стороны, значения весов скрытых слоев зависят от весов, идущих к выходному слою, поэтому данный алгоритм может быть распараллелен только на уровне подбора активационных функций или структуры сети.

Таким образом, можно сделать вывод, что при использовании данного метода обучения актуально использовать параллелизма на двух верхних уровнях — уровне подбора активационных функций и уровне подбора структуры сети.

Используемая литература

1. Крючин О.В. Подбор архитектуры искусственных нейронных сетей с использованием кластерных систем // Электронный журнал "Исследовано в России", 115, стр. 1510-1523, 2009 г. // Режим доступа: http://zhurnal.ape.relarn.ru/articles/2009/115.pdf , свободный. - Загл. с экрана.

2. Крючин О.В., Арзамасцев А.А. Параллельный алгоритм самоорганизации структуры искусственной нейронной сети // Вестн. Тамб. ун-та. Сер. Естеств. и техн. науки. 2011. – Т. 16, Вып. 1 – С. 199-200.

3. Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.

4. Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.

5. Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.

6. Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
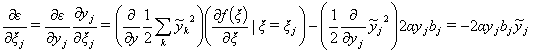
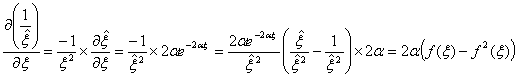